逼近定积分的再生核方法*

刘 路，吕学琴

(哈尔滨师范大学)

0 引言

在微积分中用Newton-Leibniz公式计算连续函数f(x)的定积分［1］:

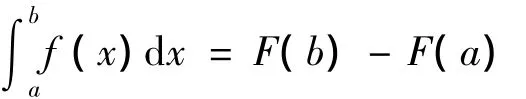
但是，当被积函数是点列(xi，f(xi))，i=1，2，…，n的形式给出时，或当被积函数f(x)的原函数F(x)不能用初等函数表示时，则无法用Newton-Leibniz公式计算，如

在微积分中，定积分是Riemann和的极限，它是分割小区间趋于零时的极限，即:

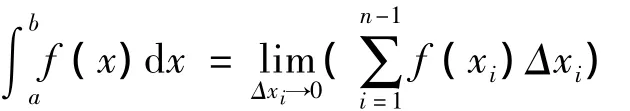
在数值积分公式中，用有限项的和近似上面的极限，通常由函数在离散点函数值的线性组合形式给出.记

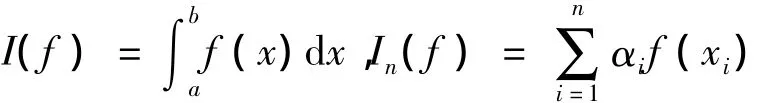
其中I(f)表示精确积分值，In(f)表示近似积分值，{xi}称为节点，αi称为系数.

该文所述内容，即为通过再生核方法［3-5］来确定In(f)中系数αi，从而构造出一种再生核方法的级数形式的数值表示.

1 再生核空间的定义

定义 1.1［5］［a，b］ ={u(x)|u(x)是［a，b］上的绝对连续实值函数，u'(x)∈ L2［a，b］}.

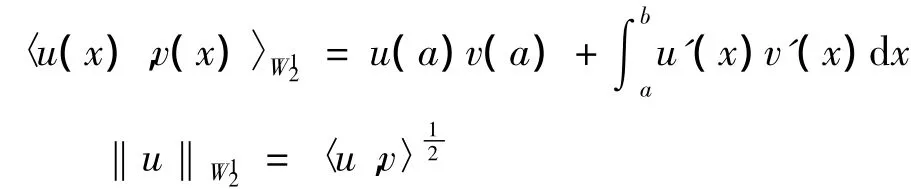
定理1.1［5］［a，b］空间是一个再生核空间，即:存在Rx(y)∈［a，b］，对任意 u(y)∈和每一个固定的 x ∈［a，b］，使得对任何 y∈［a，b］，有

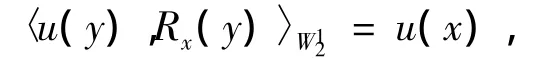
再生核Rx(y)记为:

2 再生核方法确定In(f)中的系数αi

2.1 线性有界泛函

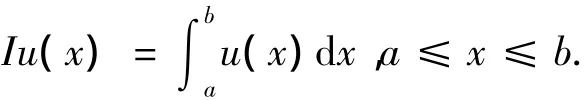
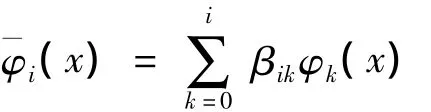
其中 βik是标准正交化系数，βii＞ 0，i=1，2，….

2.2 再生核方法求积分系数

定义投影算子Pn:［a，b］→ span{φ1，φ2，…，φn}

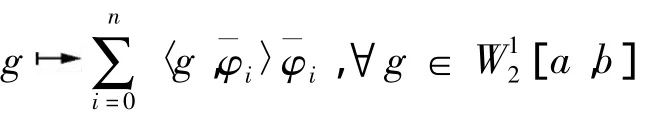
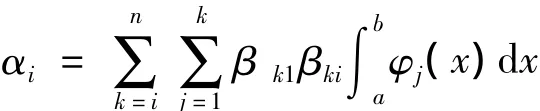
因为 φi(x)=Rxi(x)，于是

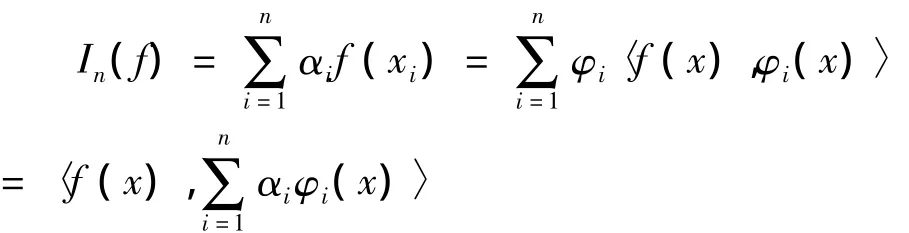
又因为

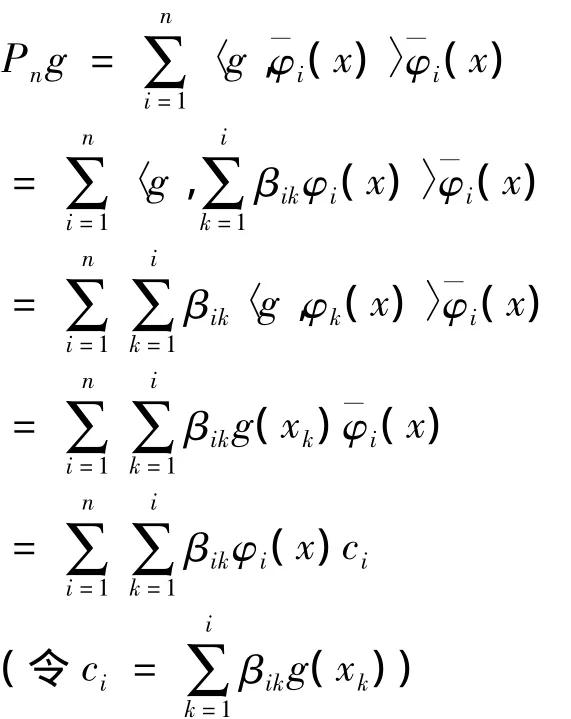
3 算例

该段给出了一个数值算例论证文章所提算法的有效性，所有的计算均是通过软件Mathematica 5.0实现得到的.

例 考虑下面积分:

使用此算法，在(0，1)上分别选取10～50个点并得到精确积分值和近似积分值的绝对误差和相对误差列在表1.

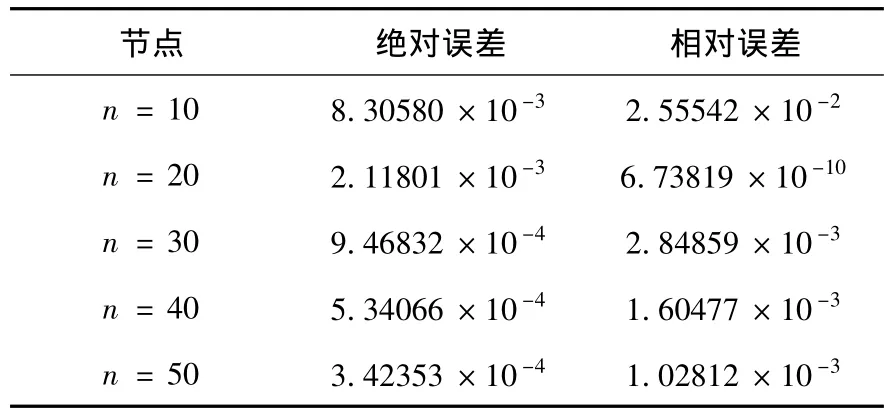
表1

［1］ 刘玉琏，等.数学分析讲义:上册.北京:高等教育出版社，2003.

［2］ 李庆扬，王能超，易大义.数值分析.北京:清华大学出版社，2001.

［3］ Chen Zhong，Zhou Yongfang.A new method for solving Hilbert type singular integral equations.Applied Mathematics and Computation，2011，218:406-412.

［4］ Cui Minggen，Lin Yingzhen.Nonlinear numerical analysis in the reproducing kernel space.New York:Nova Science Publisher，2008.

［5］ Chen Zhong，Lin YingZhen.The exact solution of a linear integral equation with weakly singular kernel.Mathematical A-nalysis and Applications，2008，344:726-734.