关于柯西-黎曼方程的几点注记*

徐助跃

(湘西自治州民族广播电视大学)

0 引言

柯西-黎曼方程的最初形式是达朗贝尔-欧拉方程，是十八世纪法国数学家达朗贝尔在复变函数积分学研究和瑞士数学家欧拉在流体力学研究中得到的两个方程，到了十九世纪，法国数学家柯西和德国数学家黎曼对这两个方程作了更深入、更详细的研究，并一直沿用至今，所以后人又把这两个方程叫做“柯西-黎曼”方程.

柯西-黎曼方程在复变函数论、物理学、数值计算等领域中具有十分重要的地位和应用价值，国内外学者关于其理论和应用的研究已取得很多成效.文献［1-3］讨论了柯西-黎曼方程在解析函数可微性与解析性、等价定理等方面的应用，文献［4］研究了柯西-黎曼方程在Stein流形上的应用，文献［5-7］讨论了柯西-黎曼方程在复Banach空间、积分学和偏微分方程等领域中有关数值计算的应用.该文将给出关于柯西-黎曼方程的两个性质定理，并逐一进行证明，然后举例说明柯西-黎曼方程在求解解析函数中的应用.

1 柯西-黎曼方程

在国内复变函数教材文献［8-9］中，大多是这样描述柯西-黎曼方程的:

设 f(z)=u(x，y)+iv(x，y)，则把

叫做柯西 -黎曼方程，简称C-R方程.

关于柯西-黎曼方程的形式，目前国内学者已经研究出了它的四种形式，分别是实形式、复形式、极坐标形式和梯度形式，文献［1］有详细的介绍，这里不一一列举.

2 柯西 -黎曼方程的性质定理

定理1 设f(z)=u(x，y)+iv(x，y)，如果f'(z)=0(z∈D)，则f(z)在区域D内为常数.

因此 u(x，y)= 常数，v(x，y)= 常数，故f(z)在区域D内为常数.

定理2 设f(z)=u(x，y)+iv(x，y)，如果f(z)在区域D内解析，且f'(z)≠0(z∈D)，则有:u(x，y)=c1与v(x，y)=c2(c1，c2是常数)是区域D内两组正交的曲线族.

下面分两种情形讨论:

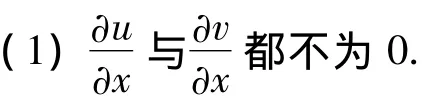
同理，可得曲线v(x，y)=c2在点(x，y)处的切线斜率为:

由柯西 -黎曼方程，在点(x，y)处有:

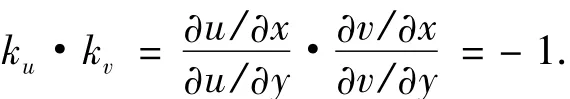
所以曲线 u(x，y)=c1与 v(x，y)=c2在点(x，y)处正交.

此时，过交点的两条切线，必然一条为水平切线，另一条为垂直切线，它们显然在交点处.

综上，u(x，y)=c1与 v(x，y)=c2是区域 D内两组正交的曲线族.

3 全微分法求解析函数

关于求解解析函数的表达式，大多数教材介绍的方法是:对于解析函数

f(z)=u(x，y)+iv(x，y)，若已知 u(x，y)，则可利用曲线积分法求出v(x，y)，反之亦然.国内学者对求解解析函数表达式的研究大多集中在对曲线积分法的进一步改进，从而得到一种相对简单的方法，并给出了一些计算公式，比如文献［10-11］等.这里，利用柯西 -黎曼条件，给出一种全微分法去求解解析函数表达式，通过与积分法的比较，可以发现该方法更为简单.

3.1 全微分方法介绍

已知某解析函数 f(z)=u(x，y)+iv(x，y)实部 u(x，y)，求虚部 v(x，y).方法如下:

对 v(x，y)求微分，得

由柯西-黎曼方程有

显然，该式是一个全微分，理由:因为u(x，y)与v(x，y)都是二元函数，易得

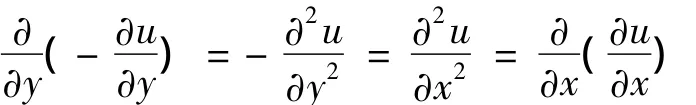
3.2 全微分法应用举例

为了体现全微分法的简单性，下面分别用曲线积分法、不定积分法、全微分法对同一个题进行解析函数表达式的求解.

例 已知解析函数f(z)=u(x，y)+iv(x，y)的实部 u(x，y)=x2-y2，求 f(z).

解法1 曲线积分法

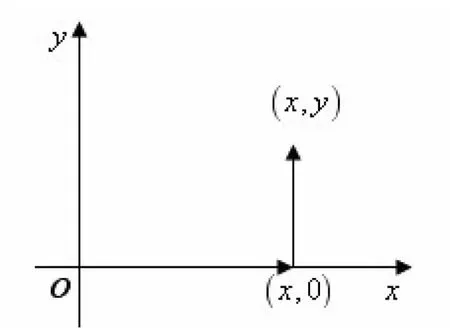
图1

从而有:

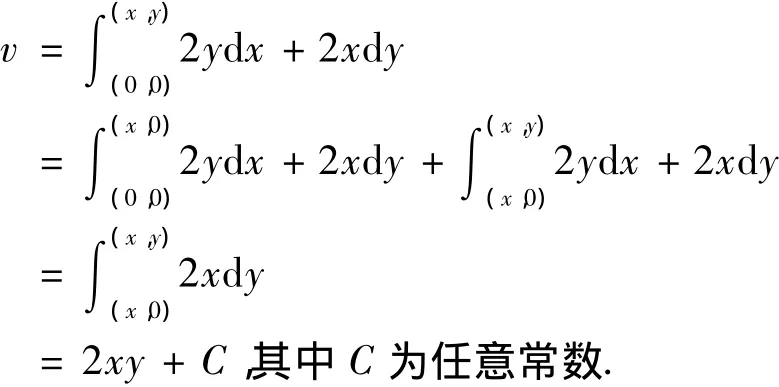
故f(z)=x2-y2+i(2xy+C)=z2+iC.

解法3 全微分法

很明显，(2)式是v(x，y)的微分式，于是

此时显然有:v=2xy+C，其中C为任意常数.故f(z)=x2-y2+i(2xy+C)=z2+iC.

［1］ 韦煜.不同形式柯西-黎曼方程的比较与分析［J］.工科数学，2002，18(4):83-87.

［2］ 徐助跃，杨先林，蒋利群.关于解析函数等价定理的几点注记［J］.华中师范大学学报:自然科学版，2012，46(4):401-405.

［3］ 李会序，王雪梅.一种新的解析函数判定定理及其在多复变中的推广［J］.河南工程学院学报:自然科学版，2011，23(2):73-75.

［4］ 邱春晖.Stein流形上Cauehy-Riemann方程的具有权的基本解［J］.厦门大学学报:自然科学版，1992，31(2):111-115.

［5］ 龚异，刘太顺.复Banach空间中C-R方程的全纯解［J］.数学学报，2002，45(1):1-6.

［6］ 马忠泰，钟同德.Cauchy-Riemann方程解的积分表示与延拓定理［J］.工程数学学报，1998，15(1):30-34.

［7］ 田益民.偏微分方程的一阶系统数值方法［J］.北京交通大学学报，2011，35(6):144-146.

［8］ 钟玉泉.复变函数论:第三版［M］.北京:高等教育出版社，2004.

［9］ 肖荫庵.复变函数［M］.北京:中央广播电视大学出版社，2002.

［10］曾招云，胡琳.由调和函数求对应解析函数的几种方法［J］.高等数学研究，2012，15(4):67-69.

［11］李志林，冯录祥.关于解析函数求法的一个注记［J］.科学技术与工程，2009，9(13):3729-3730.