模糊聚类分析在员工销售业绩评估中的应用

苗森玉

(河北农业大学)

0 引言

聚类分析是将事物根据一定的特征，并按某种特定要求或规律分类的方法.传统的聚类分析是一种硬划分，它把每个待辨识的对象严格地划分到某类中.因此，这种类别划分的界限是分明的.而实际上大多数对象并没有严格的属性，它们在性态和类属方面存在着中介性，因此适合进行软划分.1965年Zadeh教授在《Fuzzy Set》一文中提出了模糊集理论，为传统聚类分析的软划分提供了有力的分析工具.人们开始用模糊的方法来处理聚类问题，并称之为模糊聚类分析.由于模糊聚类得到的样本属于各个类别的不确定性程度，表达了样本类属的中介性，即建立起了样本对于类别的不确定性描述，更能客观地反映现实世界.［1］

模糊聚类分析包含多种分析方法，该文选取某家办公用品公司的8个销售员的数据作为统计指标，利用最大最小法建立相似矩阵，用闭包法做出聚类分析.

1 模糊聚类分析的基本思想与步骤

聚类分析的基本思想是用相似性尺度来衡量事物之间的亲疏程度，并以此来实现分类.模糊聚类分析的实质就是根据研究对象本身具有的属性来构造模糊矩阵，在这个基础之上根据一定的隶属度来确定其分类关系.其主要步骤包括确定样本统计指标、数据标准化、标定距离以建立模糊相似矩阵和聚类.［2］

1.1 确定样本统计指标

设论域 X={x1，x2，…，xn}为被分类对象，每个对象又有m个指标表示其性状，即xi={xi1，xi2，…，xim}，(i=1，2，…，n).于是，得到原

式中，xnm表示第n个分类对象的第m个指标的原始数据.

1.2 数据标准化

描述事物特征的量纲是各种各样的，为了使不同量纲能够进行分析和比较，通常需要对数据进行标准化变换，将数据压缩到［0，1］区间.常见的变换方式是先做平移-标准差变换，

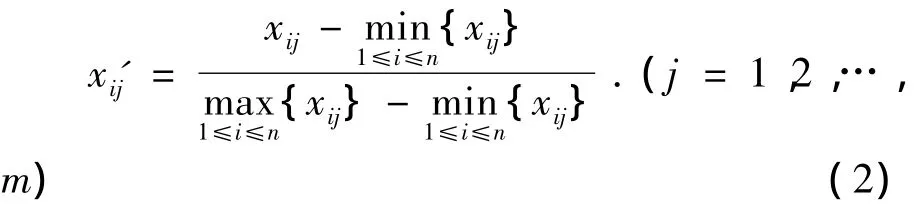
1.3 建立模糊相似矩阵

依据标准化的数据矩阵建立模糊相似矩阵，引入相似系数rij.

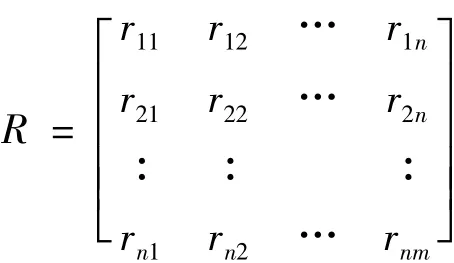
这里rij表示两个样本xi与xj之间的相似程度，当rij越接近于1，表明这两个样本越接近.rij的确定方法很多，比如相似系数法、距离法等，每一类方法又分为很多具体方法.该文选用相似系数法中的最大最小法，其计算公式为:

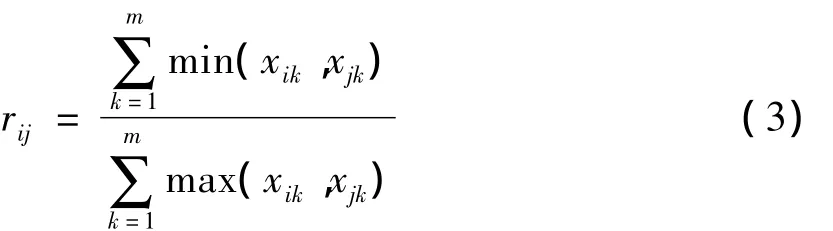
其中:rij∈［0，1］，1 ≤ i，j≤ n.

1.4 聚类

聚类的方法有多种，该文使用的是基于模糊等价矩阵的传递闭包法.一般情况下，按照上述方法建立的模糊矩阵只是一个相似矩阵R，不一定是一个模糊等价矩阵.即矩阵R具有自反性和对称性，但是不具备传递性.为了进行分类，须将R改造为模糊等价矩阵，求其传递闭包t(R)即可.其依据是下面定理:

定理 设R是n阶模糊相似关系，则存在一个最小的自然数k(k≤n)，使得R的传递闭包t(R)=Rk，且对一切大于k的自然数l，恒有Rl=Rk.［3］

该定理说明，在不超过n次运算内，即可求得R的传递闭包t(R)，从而得到一个模糊等价矩阵.为了提高运算速度，可以用平方法依次计算 R2，R4，R8，…，一定可以找到 k，使 Rk◦Rk=Rk于是，t(R)=Rk.

有了t(R)之后，下一步就是动态聚类.动态聚类的过程就是求模糊等价矩阵t(R)的λ∈［0，1］截矩阵的过程，［4］λ 截矩阵 t(R)λ是一个布尔矩阵，也是一个等价矩阵.其元素为:

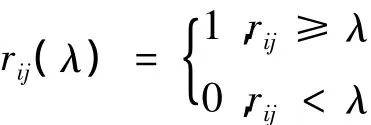
当λ从1逐渐变化到0时，t(R)不断变化，这个过程形成了一个动态聚类.

2 模糊聚类在销售评估中的应用

2.1 确定样本统计指标和数据标准化

一家国内某品牌化妆品公司销售部主管对销售员的销售业绩进行评估.该公司的销售人员通过各地奔走，派送公司产品，创办展销会，介绍新产品，打入各大商场柜台，努力增加公司产品在市场上的占有率，并且及时查处在这些销售过程与产品有关的各种问题.销售评估这类问题具有自身的特点:第一是影响因素很多，并且这些因素之间的关系错综复杂，其中一些因素因为检测手段的局限而无法测度，另一些因素信息则可以通过试验和检测等方法来获取，所以，模糊性是销售问题的显著特点;第二是由于模糊性的积累使销售评估结果的精度降低，影响评估的精确性，而模糊聚类是解决这一矛盾的有效方法之一.利用以上提到的方法，对该公司销售员的销售业绩进行细致的分析和科学的分类.

该公司8个区域销售员的数据，包括销售员所在区域，区域面积(单位:平方公里)，区域内人口数量(单位:百万)，区域内销路的数量，销售员促成定单纯利润，具体数据见表1.根据公式(1)、(2)对表1数据进行标准化处理，标准化后的数据如表2所示.

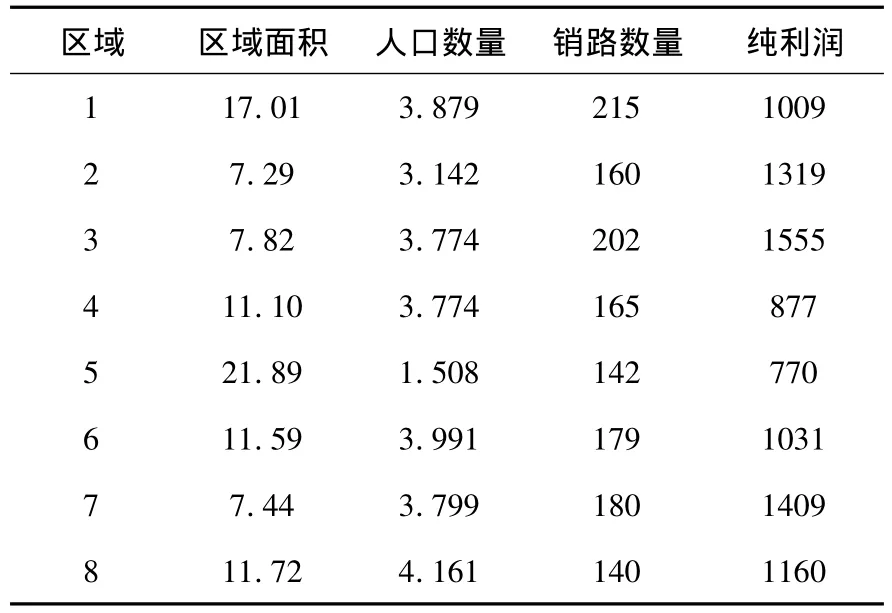
表1 各销售员具体数据表

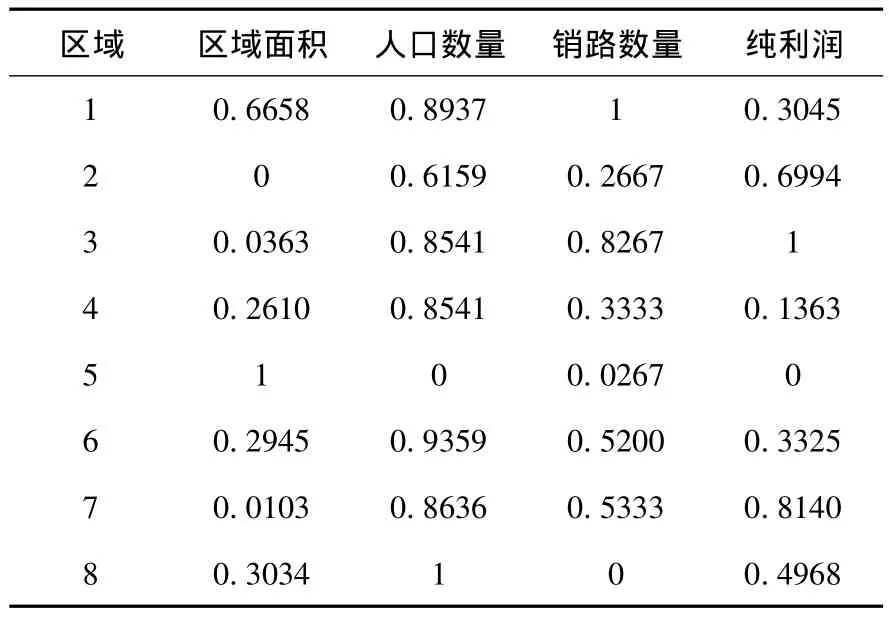
表2 各销售员具体数据的标准化数值

2.2 建立模糊相似矩阵

根据表2的数值，用最大最小法计算各销售员具体数据的相似关系矩阵R.将表2的数值代入公式(3)得

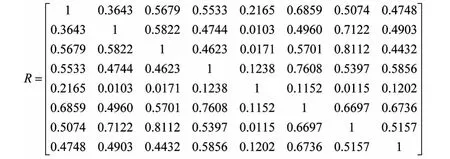
2.3 聚类分析

根据上述提到的平方法求解传递闭包可得:

此矩阵即为所求模糊等价关系矩阵.

根据模糊等价关系矩阵既可对8名销售员进行聚类分析.令λ由1降至0，按λ截矩阵进行动态聚类.

当 0.8112 ＜ λ ≤ 1 时，t(R1) =，X被分为8类:{x1}，{x2}，{x3}，{x4}，{x5}，{x6}，{x7}，{x8}.

同理，当0.7608＜λ≤0.8112时，X被分为7 类:{x1}，{x2}，{x3，x7}，{x4}，{x5}，{x6}，{x8}.

同理，当0.7122＜λ≤0.7608时，X被分为6 类:{x1}，{x2}，{x3，x7}，{x4，x6}，{x5}，{x8}

当0.6859＜λ≤0.7122时，X被分为5类:{x1}，{x2，x3，x7}，{x4，x6}，{x5}，{x8}.

当0.6736＜λ≤0.6859时，X被分为4类:{x1，x4，x6}，{x2，x3，x7}，{x5}，{x8}.

当0.6697＜λ≤0.6736时，X被分为3类:{x1，x4，x6，x8}，{x2，x3，x7}，{x5}.

当0.2165＜λ≤0.6697时，X被分为2类:{x1，x2，x3，x4，x6，x7，x8}，{x5}.

当0 ＜ λ≤0.2165时，X被分为1类:{x1，x2，x3，x4，x5，x6，x7，x8}.

上述分类结果中，按0.8112＜λ≤1和0＜λ≤0.2165分类，8名员工各自成一类和全部并为一类没有实用价值，不予考虑.其他6个分类方案中，以0.6736＜λ≤0.6859时为例，对聚类结果进行分析.此时销售员2，3，7分为一类，业绩最好，销售员8自己分为一类，业绩相对较好，销售员1，4，6分为一类，业绩较差，销售员5的业绩最差.

3 结束语

通过分析，利用上述计算方法所得出的结论与实际情况基本相同.其中销售员2、3、7虽然负责的区域比较小，但从订单利润方面看，明显较好，而负责大区域的销售员5，反而订单利润低，销售业绩差，印证了本文方法的合理性.当然，为了更切合实际，在对销售员进行评估考核时应适当考虑到销售员5所在的区域人口数量较少对其业绩的影响.总之，本文方法充分考虑了该公司销售员绩效评估的模糊性，消除了传统的评估方法采用划界指标进行硬性划分的不合理性，同时，体现了模糊聚类分析的实施步骤具有极强的规律性且容易编程实现.

［1］ 高新波.模糊聚类分析及其应用［M］.西安:西安电子科技大学出版社，2004.

［2］ 高德军，陆新春.基于聚类分析的简单高校分类方法［J］.泰山学院学报，2004.5(3):42-45.

［3］ 罗兰星.模糊聚类分析中传递闭包法及其应用［J］.四川省卫生管理干部学院学报，2005，24(2):38-42.

［4］ 李吉鸿.模糊数学基础及使用算法［M］.北京:科学出版社，2005.