修理有延迟的线性n中取n-1好系统的可靠性分析*
2013-10-24王俊元常迎香廖鸣泰
王俊元,常迎香,廖鸣泰
(兰州交通大学)
0 引言
文献[1]对n-1中取连续n-1好系统在故障部件均可以修复如新的假设下,对系统的可靠性进行了分析,得到了系统的瞬时可用度、可靠度、系统首次故障前的平均时间等可靠性指标.文献[2]研究了n中取n-1好系统在故障部件不可以修复非新,部件寿命和维修时间的分布均是指数分布,当部件的寿命越来越短,维修时间越来越长时,研究了系统的可靠性.然而在现实生活中,当部件故障后不能立即得到修理,需要等待修理.该文在文献[2]的基础上假设修理有延迟,得到了系统在上述假设下的瞬时可用度、可靠度的Laplace变换表达式以及系统首次故障前的平均时间.
定义1[3]设{Xn,n=1,2,…}是相互独立的非负随机变量序列,如果Xn的分布函数是F(an-1t),n=1,2,…,且 a > 0,则称{Xn,n=1,2,…}是一个几何过程.
当 a > 1 时,{Xn,n=1,2,…}是随机递减的;当0 < a < 1 时,{Xn,n=1,2,…}是随机递增的.
1 模型描述
(1)线性相邻n中取n-1连续好系统,由排成直线的n个同型部件和一个修理工组成,当且仅当系统中有相邻且连续的n-1个部件正常工作时,系统正常工作,否则系统故障.
(2)每次故障后部件不能修复如新,部件介于第(n-1)次修理完成和第n次修理完成的时间间隔称为部件的第n个周期.部件i在第k个周期的寿命(i=1,2,…,n)的分布函数为:当部件i-1在工作时,F0k(t)=P{≤t}=1-exp{-ak-1λ0t};当部件 i-1故障时,F1k(t)=P{≤ t}=1-exp{-ak-1λ1t},其中 t≥0,i=2,3,…,n,λ1≥ λ0> 0.当 i=1 时,规定:F1k(t)=P{≤ t}=1-exp{-ak-1λ0t}.维修时间(i=1,2,…,n)的分布函数为:Gk(t)=P{≤t}=1-exp{-bk-1ut},其中t≥0,i=1,2,…,n,u > 0,a > 1,0 < b < 1.
(3)假设部件发生故障后不能够立即得到修复,需要延迟修理,设Wn表示在第n个周期的延迟修理时间,Wn服从指数分布,用H(t)表示分布函数,H(t)=1-exp{-θt}.
(4)在t=0时,所有部件都是新的.
(6)系统故障后,未故障的部件不再发生故障.
2 模型分析
设N(t)表示系统在时刻t的状态,则有

{N(t),t≥0}是一随机过程,系统的状态空间为 E={0,1,2,…,n,-1,-2,…,-n,n+2,n+3,…,n+n,n-1,n-2,…,n-(n-1),-n+2,-n+3,…,-n+n,-n-1,-n-2,…,-n-(n-1)},系统的工作状态集为W={0,1,n,-1,-n},系统的故障状态集为F=E-W.随机过程{N(t),t≥0}不是马尔科夫过程,但是通过补充变量的方法,使其变成马尔科夫过程.用Im(t)(m=1,2,…,n)表示部件m在时刻t所处的周期,则{N(t),I1(t),I2(t),…,In(t),t≥0}是广义的马尔科夫过程,时刻t系统的状态概率定义为:
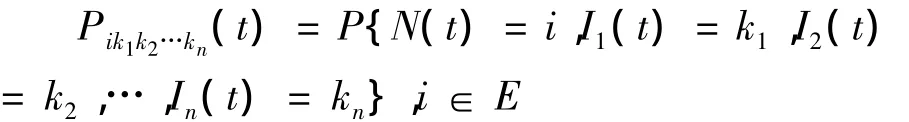
其中 k1,k2…,kn=1,2,….
根据模型假设和增补变量法有:

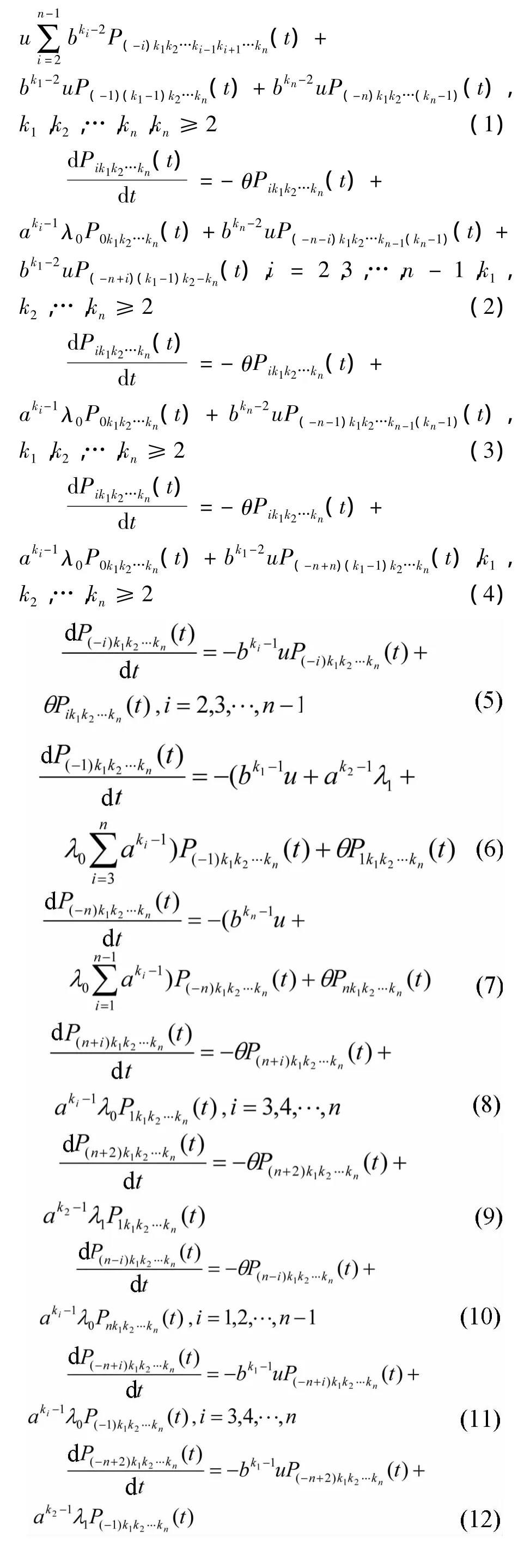
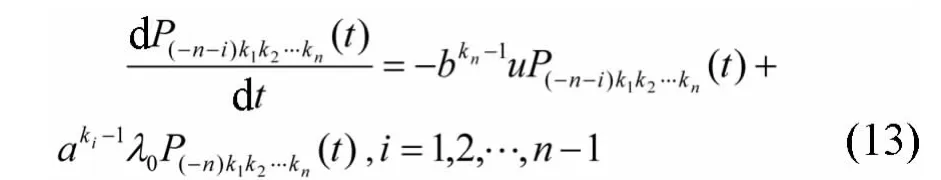
初始条件为:P011…1(0)=1;Pik1k2…kn(0)=0,i≠0;P0k1k2…kn(0)=0,k1,k2,…,kn不全为 1.

当k1=k2= … =kn=1时有:(s)=

3 系统的可靠性指标
3.1 系统的瞬时可用度A(t)
由A(t)的定义,A(t)表示为:

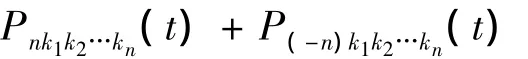
A(t)的Laplace变换表达式A*(s)为:

实际上,系统是修复非新的,这暗示着系统的可用度随时间的变化趋于零.
3.2 系统的平均故障次数Mf(t)
系统在(0,t]内的平均故障次数为Mf(t)=,其中Wf(t)表示系统的瞬时故障频度,Wf(t)的Laplace变换表达式(s)为:

3.3 系统的可靠度R(t)
设模型中的故障状态集中的状态为过程{N(t),I1(t),I2(t),…,In(t),t≥ 0}的吸收状态,定义一个新的随机过程{^N(t),^I1(t),^I2(t),…,^In(t),t≥0}.
令 Qik1k2…kn(t)=P{^N(t)=i,^I1(t)=k1,^I2(t)=k2,…,^In(t)=kn},i∈ E,则有概率分析得:

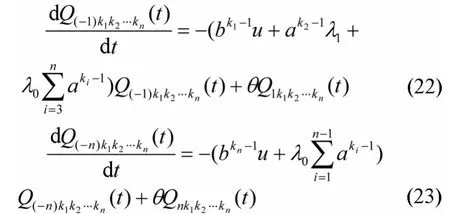
由R(t)的定义其表示为:
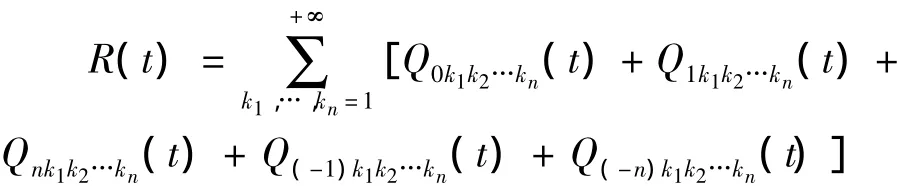
用类似的方法对式(19)到式(23)作Laplace变换得:

系统可靠度的Laplace变换R*(s)的表达式为:

特别的当k2=… =kn-1=1时,

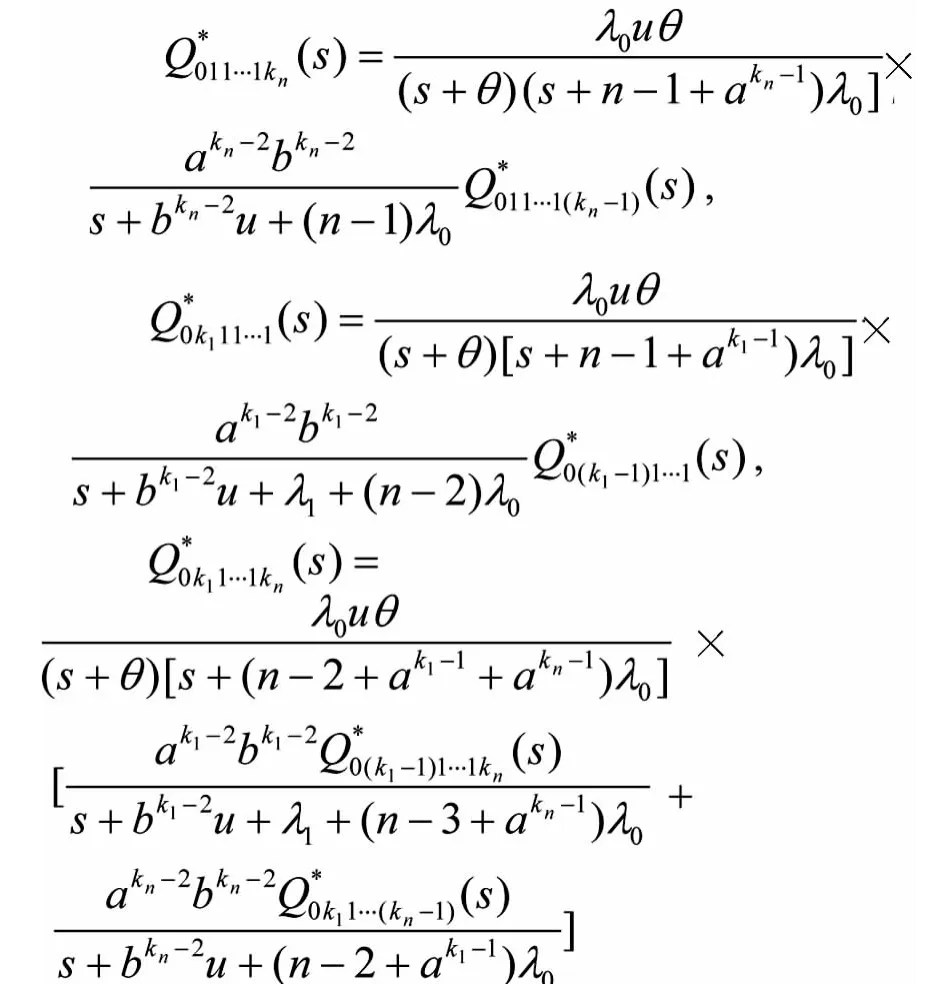
则系统可靠度的Laplace变换R*(s)的表达式为:
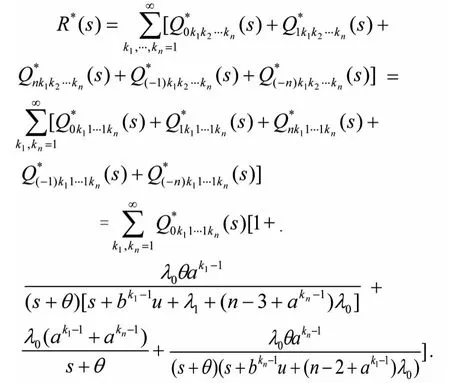
以上结果都是修理有延迟,即θ≠0时研究得到的可靠性指标,当θ=0时,系统就变成了部件故障后能够立即得到修理的情形,类似于文献[2]中的研究情形.
[1] 张元林,王太鹏,贾积身.n中取连续n-1好的可修系统可靠性分析[J].自动化学报,1997,23(6):807-810.
[2] 王旭艳,师义民.不可修复如新的线性相邻n中取连续n-1好系统的可靠性分析[J].工程数学学报,2006,23(1):87-89.
[3] 张元林.几何过程与冷储备系统分析[J].中央民族大学学报,1995(1):15-20.
[4] Zhang Yuanlin.A geometrial process repair model for a repairable system with delayed repair.Computer and mathematics with applications,2008,55(3):1630-1635.
[5] Zhao Bing,Yue Dequan.The Geometric Process Maintenance Moldel of a Series System with a Cold Standby Compontent.Journal of Information & Computational Science,2010,7(14):3085-3090.
[6] 尚勇,李伟.独立维修两部件并联系统可靠性的进一步分析[J].数理统计与应用概率,1994,9(4):93-100.
[7] 曹晋华,程侃.可靠性数学引论[M]北京:科学出版社,1986.
