基于可变加权的FCM聚类对煤炭城市分类的研究*
2013-10-24张丽娟陈孝国张亚平
张丽娟,陈孝国,张亚平
(黑龙江科技学院)
0 引言
聚类分析是统计模式识别中无监督模式分类的一个重要分支,它将一组给定的未标记的样本按照某种准则划分成多个类别,使得同一类中的样本具有较高的相似度,而不同类中的样本差别大.随着模糊理论的引入,鉴于分类本质的模糊性,人们逐步接受了模糊聚类分析.在众多的实现方法中,模糊C-均值算法(FCM)成为流行算法之一.但是初始聚类中心的选取却没有统一的方法[1-3],并且这些方法都没有考虑到不同特征对聚类的不同贡献程度.基于上述模糊聚类分析的不足,该文首先利用层次分析方法确定各个指标的初始权重;并提出了一种既能考虑到样本之间的值贴近,又能考虑到样本之间的形贴近的新的统计量——相似度,由此得到用于FCM聚类分析的初始聚类中心,并且在FCM算法中也引入了不同指标对应的权重,进而给出了一类改进的FCM聚类分析方法.
煤炭城市是指因当地煤炭资源的开发而形成和发展起来的,并且煤炭产业在城市工业结构中占有重要地位的城市.目前我国有煤炭城市64座,占到全国城市总数的9.7%,但这些煤炭城市作为我国的基本能源基地类型之一,其战略地位十分重要.在当前煤炭城市面临经济全面转轨和城市化进程当中,和其他资源城市相比,它体现的问题更为突出,已引起社会各届的关注[4-5].该文将借助改进的FCM聚类分析方法对我国的主要煤炭城市的城市化进程进行了一次系统的分类,并针对不同类型的煤炭城市提出的相应的发展策略.这对那些处在经济转型时期的煤炭城市而言,具有重要的理论意义和应用价值.
1 FCM聚类分析的改进
模糊聚类分析是以相似性为基础,主要用于研究样本的分类问题.在确定样本之间的相似系数或者距离系数时,通常都认定各个指标具有相同的权重,这与现实中的实际问题一般不符.因此就有必要考虑样本各个指标的权系数.
假定聚类问题有n个待分类的对象,每个对象有m个评价指标,对象xi=(,,…,)(i=1,2,…,n).由于各属性因子表示样本中的各种属性质量单位,其观测值可能相差悬殊,为了确保各属性因子在分析中的地位相同,要对数据进行标准化处理.经过标准化处理后,可将所有样本的各属性因子的数值都转换为0~1之间的数值.即对象变为xi=(xi1,xi2,…,xim)(i=1,2,…,n).
1.1 评价指标权重的确定
层次分析法是20世纪70年代由美国运筹学教授Saaty T L提出的.Saaty认为,若某个实际问题涉及到n个因素,要问每个因素在整体中各占多大比重?当确切依据很不充分时,就只有凭专家经验来判断了.但是只要n≥3,任何专家都可能很难说出一组确切的数据.然而,若从所有因素中任取两个因素进行比较,在行的专家一般都可以用“同等重要”“稍微重要”“明显重要”“十分重要”“极其重要”等定性语言说明其中一个因素比另一个因素对总体而言的重要性程度.Saaty建议将这些语言量化.对于给定的某个实际问题,设 X={x1,x2,…,xn}是全部因素集,可请专家对全部的因素作两两之间的对比,填写矩阵 A=(aij)n×n,其中 aij=f(xi,xj),并称 A 为判断矩阵.
下面给出一种求解权向量W=(w1,w2,…,wn)T的一种近似计算方法:
根据判断矩阵A计算出相应的特征根λmax,式中W为评价因素的权重,一致性指标CI=(λmax-n)/(n-1),式中n-矩阵的阶数,最后一致性检验CR=CI/RI,随机一致性指标RI的取值见文献[6].
若CR<0.10,可认为判断矩阵A的估计基本一致,可以接受.
若CR≥0.10,可认为判断矩阵A的估计不很一致,需要重新调整矩阵A的值,重新估计.
1.2 相似度矩阵
设两个样本评价指标向量分别为xi=(xi1,xi2,…,xim),xj=(xj1,xj2,…,xjm),定义相似度矩阵 R=(rij)n×n.其中 rij为:
1.3 初始聚类中心

由于模糊关系必须满足对称性、自反性和传递性,所以需要对相似度矩阵进行改造.利用平方法计算出传递闭包矩阵t(R).选取适当的λ,由截矩阵得出所需大致的分类,每一类样本数据的平均值记为该类的初始聚类中心.
1.4 改进的FCM算法
在实际聚类问题中,由于不同指标对聚类的作用一般是不同的,设指标权向量为W=(w1,w2,…,wm)T,则聚类样本xk与类别vt间的差异,可用广义欧氏权距离

表示.
为了更加完善地描述聚类样本xk与类别vt间的差异,将广义欧氏距离以样本xk归属于类别vk的相对隶属度 utk为权重,即 d(xk,vt)=uik‖W(xk-vt)‖.
建立目标函数

此目标函数的意义为:聚类样本集对于全体类别加权广义欧氏权距离平方和最小.
求满足目标函数的最优模糊分类矩阵U*、最优模糊聚类中心矩阵V*和指标权重W*,分三方面进行讨论.
(1)已知模糊聚类中心矩阵V及权重W,求最优模糊分类矩阵U*.
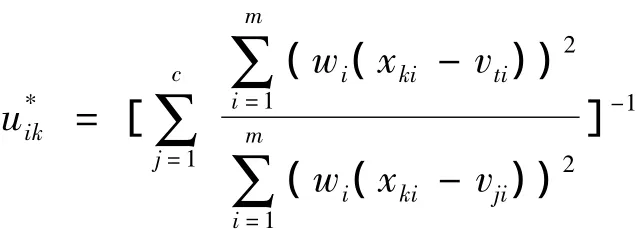
(2)已知模糊分类矩阵U及权重W,求解最优模糊聚类中心V*.
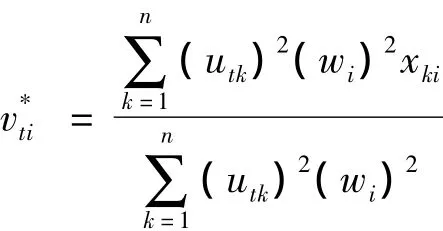
(3)已知模糊分类矩阵U及聚类中心矩阵V,求解最优权重W*.
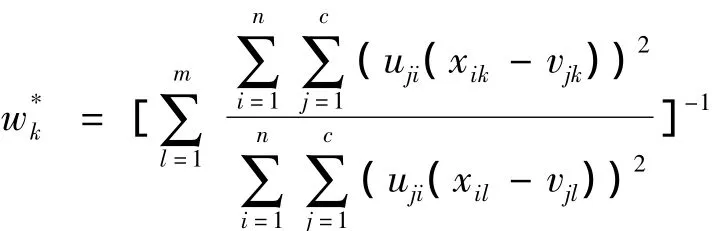
1.5 改进的FCM聚类方法的实现步骤
(1)对原始数据进行标准化.
(2)计算初始指标权重.
(3)计算相似度矩阵R.
(4)计算R的传递闭包.利用平方法计算传递闭包矩阵t(R).
(5)计算初始聚类中心矩阵V(0).选取适当的λ,由截矩阵得出初始分类矩阵,每一类样本数据的平均值记为该类的初始聚类中心.
(6)计算变化后的模糊分类矩阵U(1).
(7)计算变化后的指标权重W(1).
(8)计算变化后的聚类中心V(1).
(9)取定ε >0,若‖V(l+1)-V(l)‖≤ε则停止叠代,否则返回第(6)步继续计算,直到满足条件为止.
2 实例分析
该文选取了我国25个地级煤炭城市进行分析研究,其中反映城市化水平的指标的原始数据见表1(资料来源:2002年中国城市统计年鉴).煤炭城市城市化水平评价指标由五大类11个指标构成.具体指标含义如下:
(1)产业城市化水平:产业城市化指标选择城市化地区X1-工业增加值占GDP比重(%)、X2-第三产业增加值占GDP比重(%).
(2)经济城市化水平:经济城市化的核心内涵是经济结构的非农化,其中工业化是直接推动因素,第三产业的兴起与兴旺则是城市化向纵深拓进的表现.设置指标X3-人均GDP(元)、X4-在岗职工平均工资(元)来反映经济城市化水平.
(3)人口城市化水平:人口城市化是区域城市化的核心,也是经济城市化的直接结果和表现形式.在此,设置指标X5-人口自然增长率(‰)、X6-非农业人口比重(%)、X7-第三产业从业人员比重(%)来反映人口城市化水平.
(4)生活城市化水平:居民的生活环境、生活质量和消费水平能在一定程度上反映生活方式的城市化水平.设置指标X8-人均消费品零售额(元),X9-每十万人拥有医生数量反映生活方式城市化水平.
(5)环境城市化水平:随着城市化水平不断提高,人们也越来越重视环境保护和治理,环境状态好坏也从一个方面反映了城市化水平的高低.设置指标X10-人均园林绿地面积(平方米)、X11-建成区绿化覆盖率(%)等来描述城市环境的城市化水平.
综上所述,煤炭城市城市化水平测度从产业城市化、经济城市化、人口城市化、生活城市化和环境城市化五个方面进行了指标体系的设计,这五个方面较为系统的刻画了煤炭城市城市化水平,在实际应用中,这些指标的具体数值可以从城市统计年鉴中获得.简言之,该指标体系系统、全面、可操作性强.
根据表1中的数据,利用FCM聚类分析理论,首先将原始数据标准化,采用1.2中的方法得到相似矩阵.通过平方计算法可以快速求出Fuzzy等价矩阵.取λ=0.75得初始分类矩阵.
根据上述简单分类结果算得初始聚类中心V=(V1,V2),其中

设初始指标权向量为 w=(0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1),最后按照改进后的基于可变加权的FCM聚类方法,选取阈值ε=0.01,利用软件C++编程计算得最终分类矩阵R*.
分类结果如下:
Ⅰ类:晋城、徐州、唐山;
Ⅱ类:石嘴山、乌山、抚顺、大同、焦作、平顶山、阳泉、双鸭山;
Ⅲ类:朔州、淮南、阜新、铜川、淮北、鹤岗、萍乡;
Ⅳ类:辽源、枣庄、鹤壁、七台河、鸡西、赤峰、六盘水.

表1 25个地级煤炭城市城市化水平原始表
聚类结果表明:第一类城市的城市化水平在我国煤炭城市中是最高的.这些城市的经济发展水平高,城市化具有良好的基础.第二类城市属于城市化水平居中的城市.这类城市的典型特征是正处于由资源型城市向综合型城市的转型之中.第三类城市属于城市化水平一般的城市.第四类城市属于城市化水平低的城市,这些城市所处的区域远离经济发达地区,受外界经济辐射作用较弱,所以应该加强自身的经济转型力度.
3 结论
利用相似度矩阵代替传统模糊聚类分析中的相似矩阵,弥补了以前聚类模型中未综合考虑样本之间的值贴近程度和形贴近程度的缺陷,同时针对指标特征优先级别的不同引入了指标权重.利用相似度矩阵确定了初始聚类中心,并在FCM法中考虑了指标权重,经过深入研究给出了迭代公式和相应算法.将改进后的FCM法应用到煤炭城市分类中去,将25个地级煤炭城市按11项指标分成了三类,聚类结果对城市自身的位置和将要发展的方向都有一定的参考价值和指导意义.
[1] 张慧哲,王坚.基于初始聚类中心选取的改进FCM聚类算法[J].计算机科学,2009,36(6):206-209.
[2] 陈孝国.基于Fuzzy理论的一种医疗诊断模型[J].数学的实践与认识,2009,39(13):80-89.
[3] 陈孝国.基于遗传算法的可变加权FCM聚类方法改进研究[J].高师理科学刊,2011,31(1):12-15.
[4] 陈孝国,杨悦,孙秀娟.Fuzzy数学在采煤机故障诊断中的应用[J].煤矿机械,2007,28(5):187-188.
[5] 樊杰.我国煤炭城市产业结构转化问题研究[J].地理学报,1993.48(3):218-225.
