半张量积在布尔网络同步中的应用

张 静，樊永艳

(沧州师范学院)

1 布尔网络

近年来布尔型网络以及同步分析被逐渐运用于大型基因调节网络全局行为的分析研究，其优点是结构简单明了.另外，它在生命科学、金融科学以及其他一些典型复杂系统研究中都起到非常重要的作用.布尔网络［1-2］G(V，F)由结点状态集V={X1，X2，…，Xn}和布尔函数集F={f1，f2，…，fn}组成.结点i在t+1时刻的状态Xi∈{0，1}是由其他一些与它相连通的结点，，…在t时刻的状态，，…，决定的，即

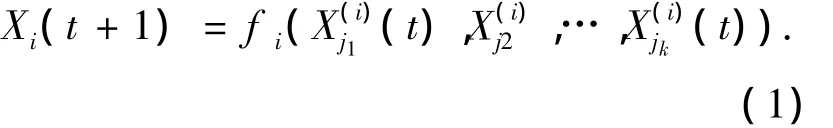
网络在t时刻的状态由所有结点的状态向量→X(t)=X1(t)X2(t)…Xn(t)来描述.很明显，对于一个有n个结点的网络，它的状态空间由00…0到11…1的2n种状态组成的.

图1 节点A和B组成的布尔网络

图1［3］是由两个节点A和B组成的布尔网络，它的动态系统为

其 中 ∨ (∧)意 思 是 max(A(t)，B(t))(min(A(t)，B(t))).

2 半张量积

矩阵的半张量积是近期中科院系统所程代展教授在文献［4］中提出的一种新的矩阵乘法，它是对普通矩阵乘法的推广.对于普通矩阵，矩阵A、B只有矩阵A的列数与矩阵B的行数相等才可以相乘.而矩阵的半张量积可以解决非等维数的矩阵相乘，即矩阵A的列数与矩阵B的行数不相等的矩阵相乘.矩阵的半张量积的应用领域很广，它主要用来处理多维数组及处理非线性问题，在逻辑、几何、代数、物理、控制系统及Morgan等等问题中均可找到它的应用［4-6］.

定义1［4］设 A ∈ Mm×n，B ∈ Mp×q.记 n 与 p的最小公倍数为t=lcm{n，p}.定义A与B的半张量积为

这里Mm×n表示所有m×n矩阵的集合，⊗表示kronecker积，▷代表左半张量积.

定义2［4］换位矩阵 W［m，n］是一个 mn × mn矩阵，定义如下:它的行和列都是由双指标(i，j)标注，列是按照索引Id(i，j;m，n)排列，行是按照索引 Id(j，i;n，m)排列，并且位于［(I，J)，(i，j)］上的元素的值为

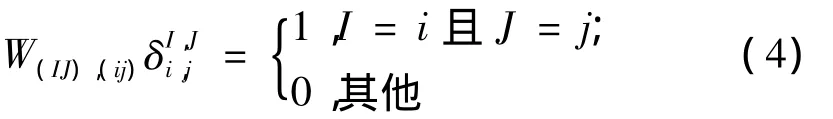
命题1［4］(1)换位矩阵的逆和转置为

(2)当m=n时，上式变为

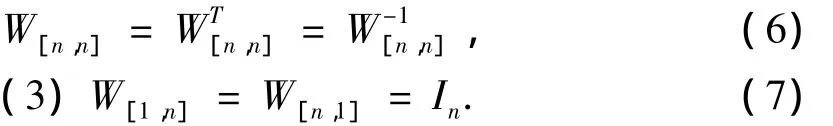
m=n的情形特别重要，为了简化符号，记

引理1［4］设A是一个逻辑变量，定义降幂矩阵为，那么对于任意的p×4q矩阵Ψ有ΨA2=ΨMrA.

定义3［4］(1)(经典)逻辑论域Dt是指

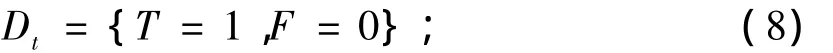
(2)(经典)逻辑变量P是指在Dt中取值的变量，即P∈Dt;

记T0≡T≡1和F0≡F≡0分别表示“真”和“假”.

定义4［4］(1)r元逻辑算子是指映射 σ:

为了使用矩阵表示，记

定义5［4］称2×2r矩阵Mσ为r元逻辑算子σ的机构矩阵，如果

考虑4个基本的二元逻辑算子;析取，P∨Q;合取，P∧Q;蕴涵，P→Q;等值，P↔Q.4个基本二元逻辑算子的结构矩阵如下:

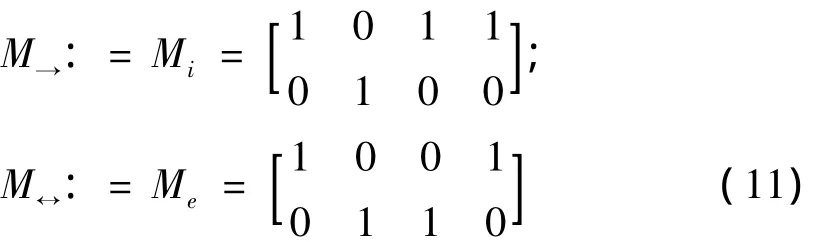
3 半张量积在布尔网络中的应用

应用半张量积，就可以将布尔网络的逻辑方程转化成为代数方程［7］，逻辑变量就表达成了向量形式，定义T=1 ～，F=0 ～，其中是单位阵In的第i列，则逻辑变量A(t)在D:={，}中取值.

对于每个逻辑算子ξ=ξ(A1，…，An)存在一个 ξ的结构矩阵，记为 Mξ∈ M2×2n，表示为

例如，对于∧和∨，分别为Mc和Md，Mc= σ2［1，2，2，2，2］，Md= σ2［1，1，1，2］.例如 A(t+1)=A(t)∨B(t)可以被表示为代数形式:

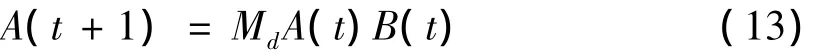
B(t+1)=A(t)∧B(t)可以被表示为代数形式:

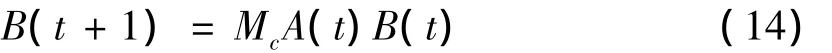
基于以上，将一个逻辑动态系统转化为一离散时间动态系统的方法，可以得到一个网络过渡矩阵L.把逻辑动态方程转化为离散时间的动态方程，一个有 n个节点 Ai，i=1，2，…，n的布尔网络被表示为

其中 ξi，i=1，2，…，n 是逻辑函数(算子).

应用(12)，Ai(t+1)=WiA1(t)A2(t)…An(t)，i=1，2，…，n，定义 x(t)=A1(t)A2(t)…An(t).可以得出

应用半张量积性质以及降幂矩阵Mr=σ4［1，4］，(16)可以被表示为x(t+1)=Lx(t).其中L被叫做过渡矩阵.

由图 1，计算其过渡矩阵，设 x(t)=A(t)B(t)，那么

则 L=Md(I4⊗ Mc)(I2⊗ w［2］)Mr(I2⊗ Mr)= δ4［1，2，2，4］

4 布尔网络的同步分析

在生态环境中，存在着许多同步现象，如夏日青蛙，知了的齐鸣，萤火虫一致发光，蟋蟀群的叫声有节奏地唱和，鸟儿成群的飞;不仅是生态，从核子到宇宙、从物理到化学，乃至人类社会，都广泛存在着同步现象，如心肌细胞和大脑神经网络的同步，钟摆同步现象，剧场中观众自发鼓掌同步等.对于复杂系统内部个体之间通过局部相互作用(耦合)，从一种状态突然变成另一种状态，逐渐的自组织形成了每个个体状态一致的现象，称作同步现象.

布尔网络可以用逻辑函数来表示，如图2.假设有一个简单的布尔网络，有四个结点，分别为A、B、C、D，并且两两相连，假设结点 A受结点 B和结点D的状态控制，节点B则受结点A和结点C的状态控制，结点C受结点B和结点D的状态控制，结点D受结点C和结点A的状态控制.如果给结点A、C“或”布尔作用，给结点B、D“与”布尔作用，分别用“0”和“1”表示结点处于“是”和“否”两种状态.

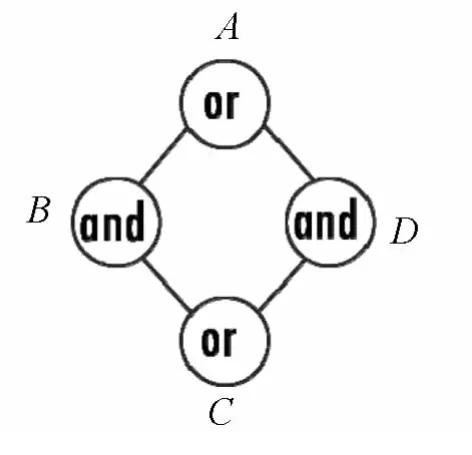
图2 逻辑函数布尔网络

则逻辑函数为:

通过给定的布尔作用，如果四个结点在某一时刻T的状态确定，则各结点在下一时刻T+1的状态也可以相应地确定，表1给出了四个结点在不同时刻可能的16种状态的真值.若在某一时刻T0，四个结点的状态均为0或1，则这个布尔网络同步.通过计算，得出，A、B、C、D初始状态为1011、1110、1111时可以达到同步状态为1，初始状态为0000时可以达到同步状态为0.其余的初始状态最终进入循环状态，达不到同步.

表1 逻辑函数布尔网络真值表

利用逻辑算子研究布尔网络的同步.

一个逻辑变量是指一个命题，如果这个命题是真的，就说这个逻辑变量取值为“真”或“1”，如果这个命题是假的，就说这个逻辑变量取值为“假”或“0”.

对于上面的四个节点有布尔作用的网络同步问题，可以把每个节点的状态看成一个逻辑变量，状态为1代表这个命题是真的，状态为0代表这个命题是假的.

可以将以上问题转化为以下逻辑方程:

若在T+k时刻网络同步，则A、B、C、D四个逻辑变量在T+k时刻同时取值为“真(即1)”或“假(0)”.那么，应用逻辑算子，给出(19)式和(20)式:

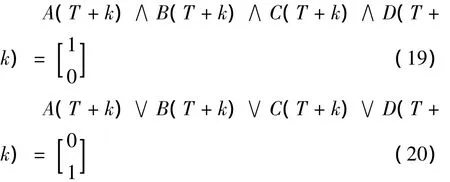
对(19)式在T+1时刻的逻辑值，有如下计算:

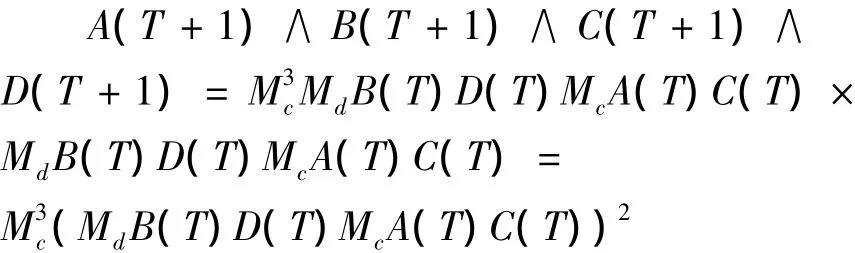
根据(21)式可以得出ac(b+d-bd)=1，则共有三个解:

这就意味着，对于在T时刻为上面解中的三种状态时，在下一时刻该网络可以达到同步状态为1.同样地，可以用式(20)解出，对于在T时刻四个结点状态只有为0000时，在下一时刻该网络可以达到同步状态为0，与真值表分析法结果相同.

在第3部分中，介绍了一个逻辑函数，可以找到一个过渡矩阵L，使下一状态x(t+1)=Lx(t).对于一个已知的初始状态，在何时可以达到同步状态为1的问题，可以归纳为解x(t)=的问题.同样的，当 x(t)=时，可以达到同步状态为0.

［1］ Liang S，Fuhrman S，Somogyi R.A general reverse engineering algorithm for inference of genetic network architectures［J］.In Paciac Symposium on Biocomputing，1998，3:18-29.

［2］ Pal R.Generating Boolean Networks with a Prescribed Attractor Structure［J］.Bioinformatics，2002，18:261-274.

［3］ Cheng D.Controllability and Observability of Boolean control networks.IEEE Trans，2009，45:1659-1667.

［4］ 程代展，齐洪胜.矩阵的半张量积［M］.北京:科学出版社，2007.

［5］ Cheng Daizhan.Semi-tensor product of matrices and its app lication to morgen’s problem［J］.Science in China(Series F)，2001，44(3):195-212.

［6］ Cheng Daizhan.Some application s of Semi-tensor product of m atrices in algebra［J］.Computers and Mathematics with Applications，2006，52:1045.

［7］ Zhou J，Chen T.Synchronization in general complex delayed dynamical Networks IEEE Trans on Circuit System，2006，53(3):7332-44.