无线传感器网络中定位技术的研究*
2013-10-24鹿建银王华本
鹿建银,王华本
(安徽新华学院)
0 引言
无线传感器网络(Wireless Sensor Network,WSN)是近年来一个热点研究领域,其中传感器网络节点定位技术也越来越受到人们的关注,这是因为传感器网络的大量应用都依赖于节点的位置信息,应用在军事领域,如对敌方坦克、步兵等各种军事力量进行定位和跟踪,以便做出相应决策;在智能医疗中,实现资源共享、互相协作、临床诊断等;可对山体、河流等监控对象,通过采集监控对象微观变化,为研究人员提供可靠的研究信息,如保护黄山迎客松,用监测迎客松周围环境的光照、湿度、风速、雨雪感知和土壤水分等信息;此外,无线传感器网络在零售、物流、食品、建筑、电网、家居、交通[1-2]等行业,也有着广泛的应用.因此,研究无线传感器网络节点定位技术具有重要意义.
1 经典无线传感器网络定位技术研究
全球定位技术:70年代,由美国海陆空三军联合研制的全球定位系统(Global Positioning System,GPS)[3],由24 颗人造卫星组成,到 1993年共耗资300亿美金,定位精度可达到15 m以内,覆盖范围达到地球表面的98%,但是为网络中所有节点都安装 GPS设备,会受到成本、功耗、扩展性等问题的限制,甚至在某些场合如室内几乎无法实现.局部定位算法:基于RFID[4-5]技术,由于设备识别的传输距离有限,主要用于物流、物品跟踪、人员登记等领域.WiFi定位算法,类似于Zigbee定位技术,但是相对于Zigbee,WiFi的突出优势在于数据传输速率更快,更易互联,较易实现交互性.超宽带(Ultra-Wideband,UWB)[6]是一种无载波通信技术,穿透能够强,最终的定位精度能够达到厘米级别,但目前技术尚不成熟.测距定位算法:主要有接收信号强度 (Received Signal Strength Indicator,RSSI)算法、到达时间 (Time of Arrival,TOA)算法、到达角度(Angle of Arrival,AOA)算法、到达时间差(Time Difference of Arrival,TDOA)算法等.测距定位机制由于借助节点之间的距离或者角度信息,通常定位精度相对较高,但同时也要求硬件支撑.非测距算法:由南加州大学Nirupama Bulusu等提出的一种基于网络连通性的质心算法(Weighted Centroid),该算法仅能实现粗粒度的定位,且要求有较高的锚节点密度才能实现精确定位.由弗吉尼亚大学He等人提出的近似三角形内点测试(Approximate Point-In-Triangulation Test,APIT)定位算法,定位精度相对较高,但需要较高的锚节点密度和较高的节点密度.哥伦比亚大学Shang Yi等人提出的基于多维标度(Multidimensional Scaling,MDS)定位算法,用迭代优化来提高定位精度等.非测距定位受环境影响较小,硬件成本低,适合于大规模网络[7-8].
2 DV-Hop定位算法分析
2.1 DV-Hop定位算法原理
DV-Hop定位算法原理与距离向量路由算法的思想非常相似,其算法过程分为三个阶段:第一阶段,先使用典型的距离矢量交换协议,使网络中所有节点获取与锚节点的跳数值.
第一阶段结束后,所有节点都会获取一个到锚节点的最小跳数值.
第二阶段,如式(1)所示:用hdi来计算锚节点i和周围待测节点的距离.
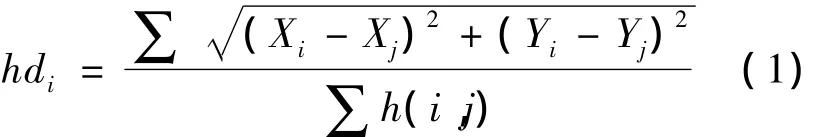
式中(Xi,Yi)、(Xj,Yj)是锚节点 i、j的坐标值,h(i,j)是锚节点i与锚节点j之间的跳数.第二阶段结束后平均每跳距离的估算值可以计算出真实距离.
第三阶段,当待测节点获得3个或更多锚节点的距离后,利用三边测量法(或者极大似然法)计算其位置,如式(2)所示:

式(2)是计算某待测节点坐标的二元二次方程组,理论上最少已知三个锚节点坐标即可保证方程组能求出唯一一组解.
由式(2)得到的展开式(3)如下:
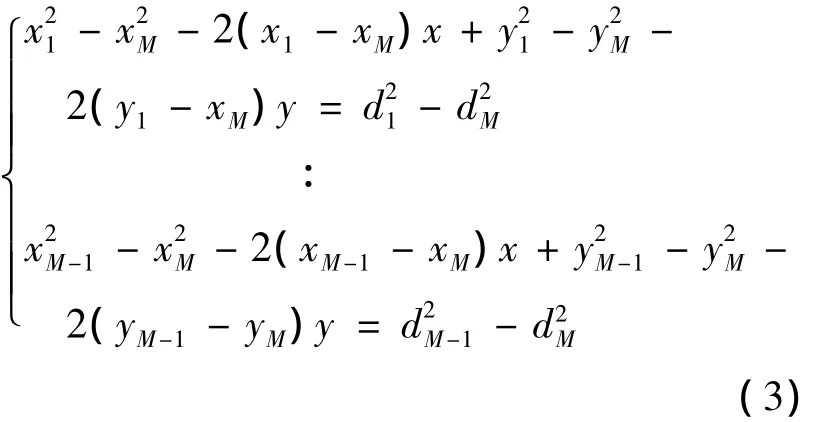
将式(3)采用矩阵AX=b方式表示,推导出式(4):

最小方差矩阵估算待测节点的坐标如式(5)所示:

2.2 改进算法
2.2.1 最小均方误差准则

式(6)是基于无偏估计准则计算平均每跳距离公式,即式(7)恒等于零.
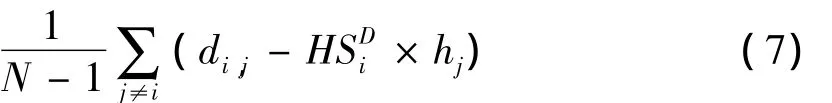
式(7)中N表示锚节点个数,估计误差均值为零,然而,根据参数估计理论,使用均方误差比使用方差更合理.因此,提出基于最小均方误差准则来计算平均每跳距离,如式(8)所示:


2.2.2 锚节点选择策略
如图1所示,平面上任意三点组成的三角形,如果最长边用lmax,那么该边所对应的高则为最小的高用hmin表示.选择hmin与lmax的比值来衡量三角形的共线程度,简称共线度,并用DC表示,如式(10)表示:


图1 三角形共线度示意图
通过分析,共线度的取值范围为[0,1],并且共线度取值越小表示三点越接近共线程度:当三点完全共线时,三角形退化,此时的共线度为0;当是等边三角形时,共线度值为1.在实际的锚节点选择过程中,可以通过设定三角形共线度来约束锚节点之间的拓扑关系,过滤掉使定位误差较大的节点,优化通信范围与跳距之间的关系,提高定位精度.
3 仿真结果及分析
该课题的仿真环境是WINDOWS XP操作系统,JDK6.0版本,仿真软件OMNeT++4.1,通信半径为100;测试区域为一个800×500的平面,30个节点随机分布在该区域内.仿真了相对定位误差,平均定位误差两种情况.在仿真过程中,为了不失一般性,DV-Hop定位误差和改进算法后的定位误差,皆取同一分布,结果取5次仿真结果的平均值.

图2 相对定位误差示意图
从图2相对定位误差示意图中可以看出,在相同的通信半径和锚节点比例下,改进算法的节点相对定位误差减小.由图3平均定位误差示意图可知,在相同通信半径和相同锚节点比例的情况下,改进算法节点定位均方差优于DV-HOP算法.

图3 平均定位误差示意图
4 总结与展望
针对DV-HOP定位算法的定位精度不高的局限性,提出了一种改进算法,该算法在距离估计和定位计算两方面进行改进,并通过改进锚节点选择策略,优化网络拓扑结果,调整通信范围和跳数之间的关系.仿真结果表明在不同的通信范围和参考节点比例下改进方法有效地减少了节点定位误差.
在后期的工作中研究算法在提高定位精度的同时,考虑如何减少节点的通信量和计算量,从而最大程度地延长网络的寿命和提高算法的实用价值.
[1] 崔丽,刘强,李栋.物联网系统及核心设备[J].中国计算机学会通讯,2010(4):18-22.
[2] Guo Zhongwen,Guo Ying,Hong Feng,et al.“Perpendicular Intersection:Locating Wireless Sensors with Mobile Beacon”.29th IEEE Real-Time Systems Symposium RTSS,2008.93-102.
[3] 张明华.基于WLAN室内定位技术研究[D].上海交通大学,2009:50-56.
[4] 李德仁,龚健雅,邵振峰.从数字地球到智慧地球[J].武汉大学学报(信息科学版),2010,35(2):127-132.
[5] Wang F,Liu S,Liu P.Complex RFID event processing[J].The VLDB Journal,2009,18,913-931.
[6] Wu D,Bao L,Du M,et al.Design and Evaluation of Localization Protocols and Algorithms in Wireless Sensor Networks Using UWB.Performance[C].Computing and Communications Conference(IPCCC),Austin,Texas,USA,7-9 Dec,2008:18-25.
[7] Shen Mingyu,Zhang Yin.DV-HOP localization algorithm based on improved average hop distance and estimate of distance[J].Application Research of Computers,2011,28(2):648-650.
[8] Wang Xinsheng,Zhao Yanjing,Li Haitao.Improved study based on DV-HOP localization algorithm[J].Computer Science,2011,38(2):76-78.
