矩函数在风速Weibull分布参数估计中的应用

郝晓弘，王海鹏 ，陈 伟，肖 骏 ，王维洲

（1．兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050；2．甘肃电力科学研究院，甘肃 兰州 730050）

0 引言

在可再生能源的开发利用中，风能是一种发展最快的清洁能源。开发利用风能有助于实现能源的安全性和多元化，减少温室气体的排放，减少化石燃料造成的环境污染。在风能开发利用中，风能资源评估是风电场建设的前提和基础。

风速的风频分布实际上就是风速的统计概率分布，是衡量风能资源分布特性的重要指标，它反映了风电场某个时段每一风速出现的概率。通常用于拟合风速分布的模型很多，经国内外广泛研究表明，双参数Weibull分布适用于对风速作统计描述［1］。只要给定了Weibull分布参数k和c，就能方便地求得体现风能资源状况的风能特征指标，如平均风能密度、有效风能密度、风能可利用小时数等。目前，估算Weibull分布参数的方法有多种，如常用的最小二乘法、均值和方差估计法、平均风速和最大风速估计法等［2］。而本文基于“Weibull分布的随机变量的各阶矩仍然服从Weibull分布”这一统计学特性，提出采用矩函数法计算Weibull分布参数，同时给出了参数估计经验公式。在算例中通过比较由风速概率分布推算出风能特征指标的估计值与由历史风速数据序列获得的实测值，说明矩函数法计算Weibull分布参数具有较高精度。

1 风速概率分布模型

Weibull分布是一种单峰、两参数的分布函数簇，其概率分布密度函数图形如图1所示。

Weibull概率密度函数为：

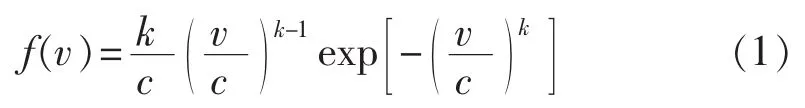
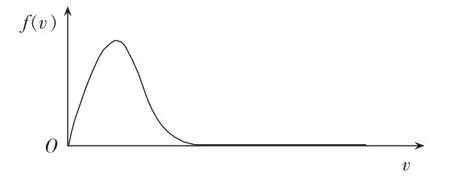
图1 Weibull概率密度函数图Fig.1 Weibull probability density function

Weibull分布函数为：

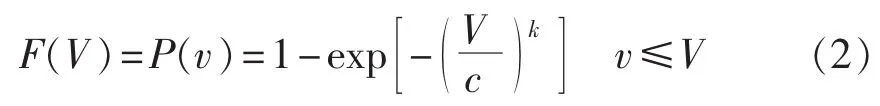
其中，v 为实测风速（m /s）；V 为给定风速（m /s）；k 为形状参数；c 为尺度参数（m /s）；P（v）为风速在有效风速区间（v≤V）的概率。

只要给定Weibull分布参数k和c，风速的分布形式和风能的特征指标也随之确定。

2 均值和方差估计法

在常用的参数估计方法（最小二乘法、均值和方差估计法、平均风速和最大风速估计法等）中，通过对比发现均值和方差估计法效果最好［2］。现将该方法介绍如下。

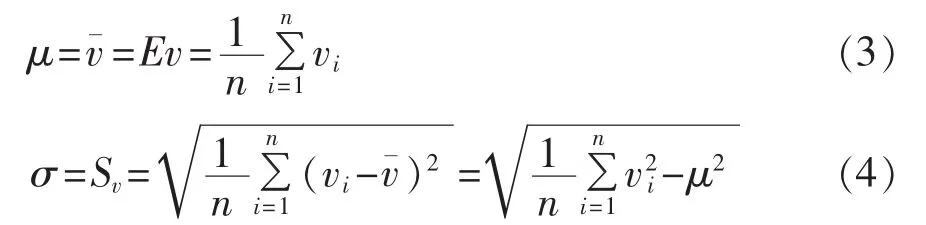
其中，vi为计算时段中每次的风速观测值；n为观测总次数。

由于：

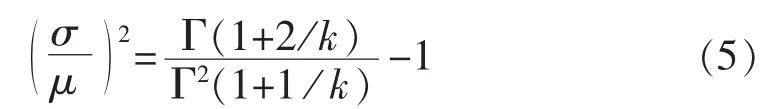
所以已知所测风速数据的μ、σ，便可求解k。一般按式（6）近似求解 k，按式（7）计算 c。

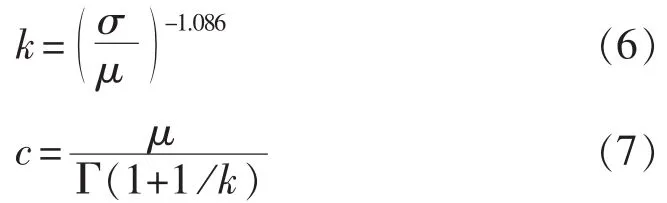
其中，Γ（·）是伽马函数。

伽马函数的定义［3］是：

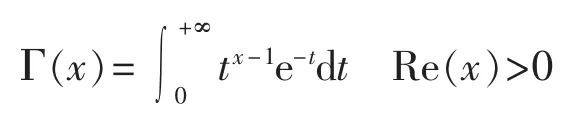
3 基于矩函数的参数估计方法

3.1 矩的概念

设 X 是随机变量，若 E（Xk）（k=1，2，…）存在，称它为X的k阶原点矩；若E｛［X-E（X）］k｝（k=2，3，…）存在，则称它为X的k阶中心矩。显然，X的数学期望E（X）是X的一阶原点矩，方差D（X）是X的二阶中心矩。

3.2 基于风速原点矩的参数估计

风速v作为随机变量，其对原点离差的n次方的数学期望，称为v的n阶原点矩，记为Evn，即：

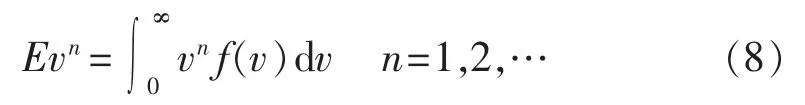
代入式（1），得：

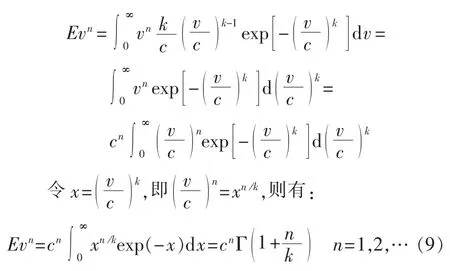
式（9）表明，风速v的n阶原点矩的分布仍为Weibull分布，只是其形状参数变为k/n，尺度参数变为cn。

将 Evn与（Ev）n做商，得：

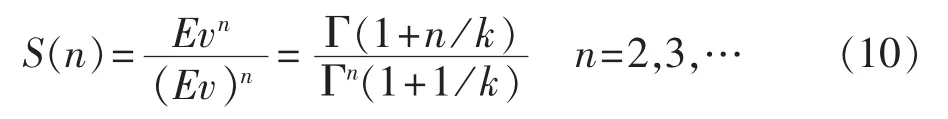
式（10）表明，当给定值 n 后，S（n）仅是 k 的函数，而S（n）可由实测风速资料得到，因此，可由实测风速资料确定k值，然后利用式（7）计算c值。但由于涉及伽马函数，直接由式（10）求解k值比较困难，本文通过确定 S（n）与k之间的关系，建立计算k值的经验公式。

大量的风速观测表明，k值的范围为1.5～2.2。为了提高适应性，本文将k值的范围扩展到0.8～5.0，步长取 0.01。通过MATLAB仿真计算，当n分别等于 2、3 时，S（n）计算结果见表 1。

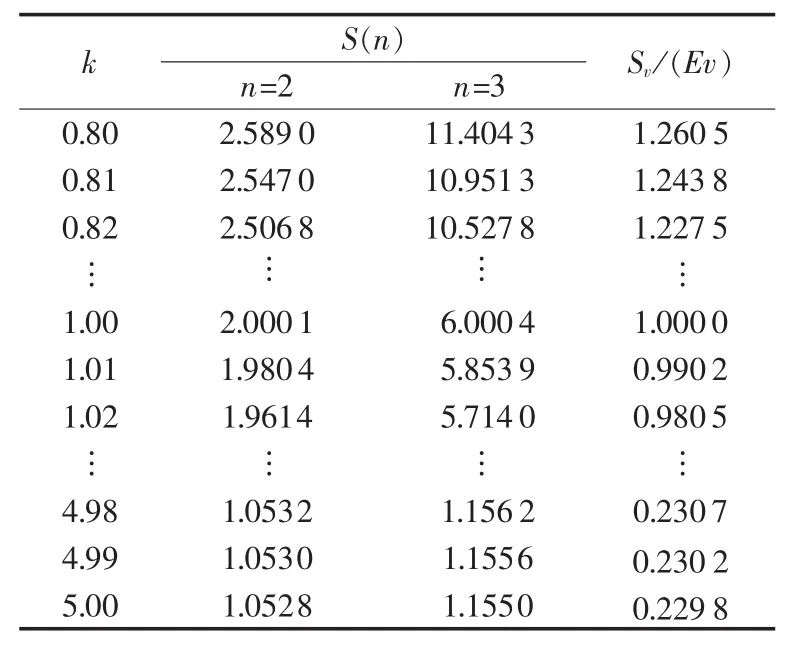
表1 k 与 S（n）、Sv/（Ev）的关系Tab.1 Relationship among k，S（n） and Sv/（Ev）

由表1中相对应的数据通过数学拟合便得到k的经验公式，式（11）、（12）分别为基于风速二阶和三阶原点矩的k值经验公式。

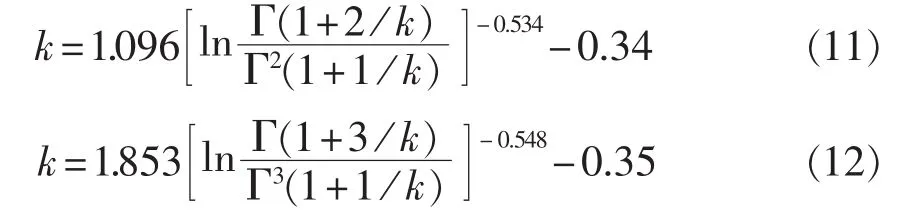
以上经验公式拟合结果见表2，拟合误差统计见表3，拟合效果分别见图2和图3。结合式（10），可将经验公式进一步变为式（13）、（14）。

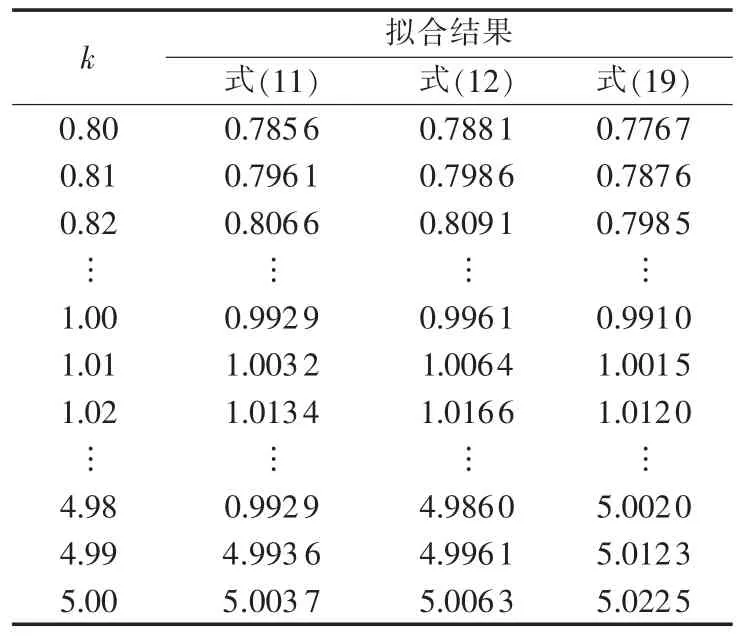
表2 经验公式拟合结果Tab.2 Fitting results of k

表3 经验公式拟合误差统计表Tab.3 Statisitics of empirical formula fitting errors

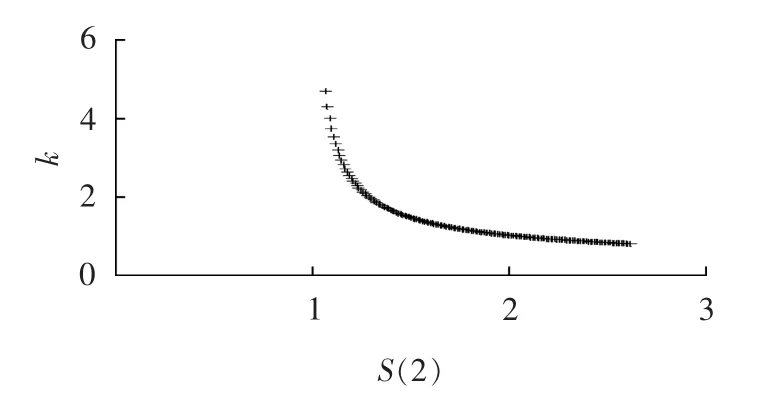
图2 经验公式（11）拟合曲线Fig.2 Fitting curve of empirical formula（11）

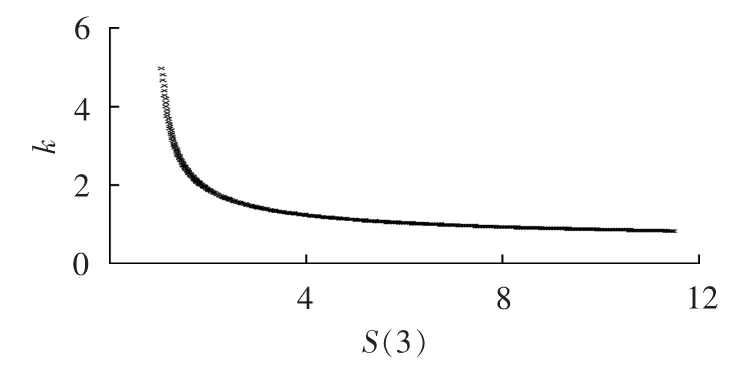
图3 经验公式（12）拟合曲线Fig.3 Fitting curve of empirical formula（12）

3.3 基于风速中心矩的参数估计

风速v作为随机变量，其对分布中心Ev离差的n次方的数学期望，称为v的n阶中心矩，并且记为E（v-Ev）n，即：

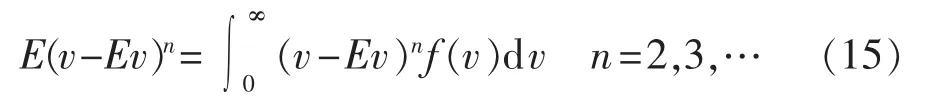
由于式（15）展开相对较为复杂，本文只讨论当n=2时的情况。风速二阶中心矩即为方差Dv，则有：

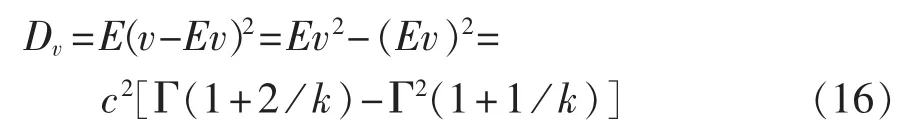
根据标准差Sv与方差Dv之间的关系：

联立式（9）、（16）、（17）得：

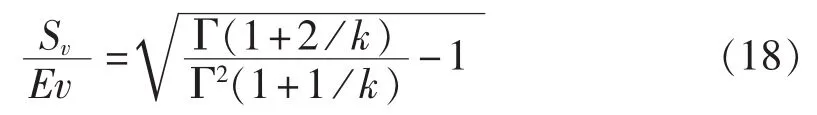
仿照 3.2节中的方法计算 Sv/（Ev）（结果见表 1），同时通过数学拟合得到计算值k的经验公式如式（19）所示。

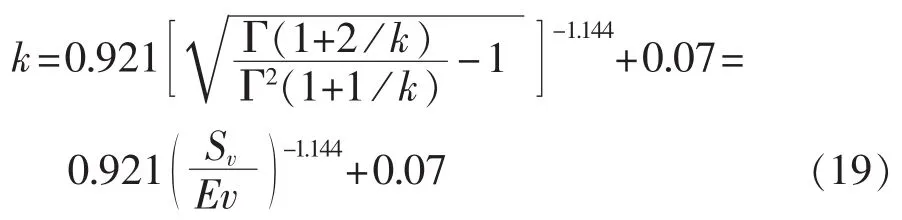
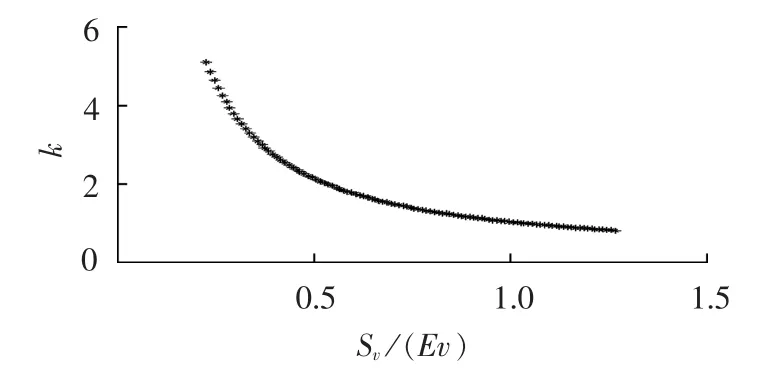
图4 经验公式（19）拟合曲线Fig．4 Fitting curve of empirical formula（19）

式（19）拟合结果见表2，拟合效果见图4，拟合误差统计见表 3。其实，式（19）和式（6）（均值和方差估计法）本质上是一致的，差别就在于公式系数的多寡，从而导致最终计算精度的高低，式（19）可以作为式（6）的改进。

4 风能特征指标

评估风电场的风能资源状况，需要计算体现风能资源状况的风能特征指标，如平均风速、平均风能密度、风能可利用小时数、平均有效风能密度等，利用风速概率分布或历史风速记录数据计算这些指标，从而为风电场建设项目的可行性研究提供依据。

用矩函数法解出风速概率分布后，可根据Weibull分布计算上述风能特征指标，计算公式［4］如下。

平均风速：

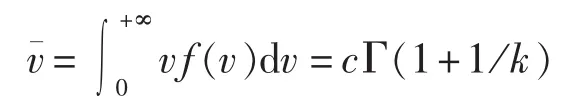
平均风能密度：

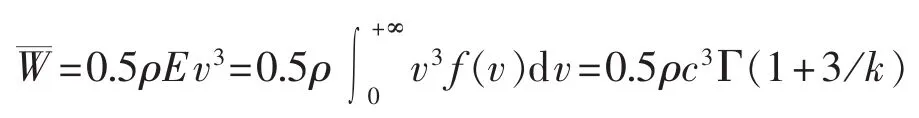
风能可利用小时数：

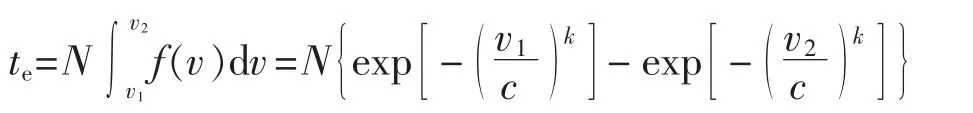
平均有效风能密度：

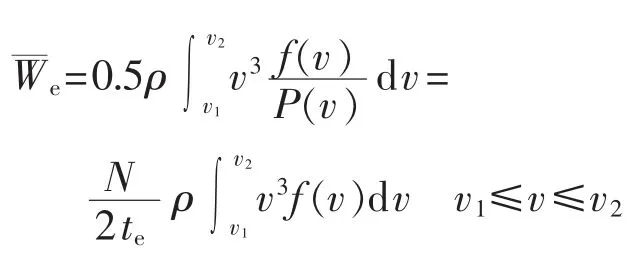
其中，ρ为年平均空气密度（kg /m3）；v2、v1分别为有效风速范围的上、下限，一般分别取25 m/s和3 m/s；N为年统计时间，一般取N=8 760 h；P（v）为风速在有效风速区间［v1，v2］的概率。

5 某风电场算例

统计河西某风电场内70 m高风塔2010-01-01至2010-12-31一整年风速资料为：Ev=6.8590m/s，Ev2=61.241 5 m2/s2，Ev3=652.9344 m3/s3，Sv=3.767 8。

分别以均值和方差估计法、矩函数法来估计Weibull分布参数k和c，并据此计算风能特征指标，同时给出了直接由风速数据统计出的各项特征指标，用于比较各方法的精度，如表4所示。

风能的大小用风能密度来衡量，它与风速的立方、空气密度成正比。风速每增加1倍，风能密度就增加8倍。因此风能密度在风能资源评估中占据重要地位。从表4中可以看出，基于矩函数法计算结果误差整体较小，精度明显高于均值和方差估计法。此外，二阶中心距法（式（19））可以作为均值和方差估计法（式（6））的改进。

表4 各种方法的参数估计结果对比Tab.4 Comparison of estimates among different methods

6 结论

风速的风频分布实际上就是风速的统计概率分布，是衡量风能资源分布特性的重要指标，它反映了风电场某个时段每一风速出现的概率。双参数Weibull分布适用于对风速作统计描述，在风能资源评估中得到了广泛应用。针对Weibull分布参数的计算，本文创新点在于基于矩函数的方法遵循了Weibull分布的统计学特性，精度检验及算例均显示，本文给出的3个经验公式对于风能特征指标计算有较高精度，且适应范围较广、计算简便，同时，二阶中心距法（式（19））可作为均值和方差估计法（式（6））的改进。此外，三阶原点矩估计法体现了风能密度正比于风速立方这一重要特性，将风能计算作为整体考虑，减少了中间过程带来的误差。