基于暂态零序电流时频特征量的配网故障选线方法
2013-10-24束洪春朱梦梦黄文珍段锐敏
束洪春 ,朱梦梦 ,黄文珍 ,段锐敏 ,董 俊 ,高 利
(1.昆明理工大学 电力工程学院,云南 昆明 650051;2.哈尔滨工业大学 电气工程与自动化学院,黑龙江 哈尔滨 150001;3.昆明理工大学 机电工程学院,云南 昆明 650093)
0 引言
中性点经消弧线圈接地的配电网系统发生单相接地故障时,因故障电流较小和电弧不稳定因素,使得基于稳态量的选线方法在实际应用时效果不甚理想。此外,由于导线坠地、树木与架空馈线接触引起的高阻故障时有发生,使得实际运行中常常存在漏选和误选。而故障后的暂态分量相比稳态分量有很大的优势,利用暂态量进行选线成为故障选线方法之首选[1]。
目前,众多学者已提出多种暂态量故障选线方法,主要利用暂态零序电流突变量、能量、幅值及极性等[2-13],使得选线效果不同程度上得到改善。利用小波包分析工具能够很好地刻画暂态零序电流信号的时频特征,文献[5-7]利用小波包分解,按照能量最大的观点确定各条馈线故障暂态零序电流的特征频带,并根据故障馈线与健全馈线的暂态电容电流在特征频段的相似性最弱的原理,形成故障选线保护判据。文献[14]提出了一种利用衰减直流分量进行选线的方法,可以作为暂态高频分量不足时的辅助选线判据。然而,配电网在缆-线混合馈线发生单相接地故障时,由于电缆线路单位长度对地电容较架空线路大很多倍,而且依频特性不同,同时缆-线混合线路存在波阻抗不连续点,这些都增加了暂态信号的复杂性。因此,在小角度故障情况下,流过健全电缆线路与流过健全架空线路的故障零序电流相似性变差且幅值有可能相近,此时暂态量很小,使得选线困难。
由于消弧线圈的补偿作用,故障零序电流可能出现倒相现象,以及电流互感器(TA)饱和引起二次电流失真等多种因素的影响,本文选取各馈线故障后1/4工频周期时窗的故障暂态零序电流数据,经小波包分解并将其重构至不同频段,进而求得的时频特征量能在短时频窗内充分反映信号的时频特性,利用相关系数表征零序电流信号的时频特性及其变化规律,并结合综合相关系数构成选线判据。
1 中性点经消弧线圈接地的配电网单相接地故障特征分析
中性点经消弧线圈接地的配电网发生单相接地故障后可利用如图1所示的等值回路分析接地故障暂态过程,考察故障接地电流的暂态特性。
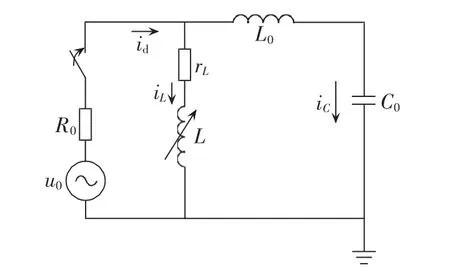
图1 经消弧线圈接地配电网单相接地时暂态电流等值回路Fig.1 Equivalent circuit of transient current for single-phase grounding fault of distribution system grounded with arc suppression coil
在分析暂态电容电流时由于其自由振荡频率很高,同时消弧线圈的电感L≥L0,因此等效电路图中的rL与L可忽略不计。单相接地故障发生瞬间,就相当于一个零序正弦电压 u0(t)=Umsin(ωt+φ)接入图1所示等效电路中,则:
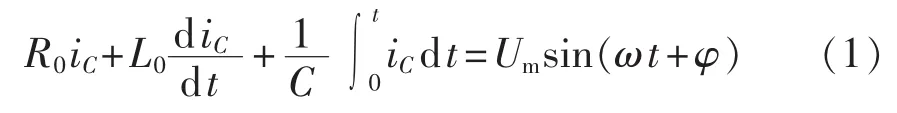
经拉普拉斯变换得到电容电流瞬时表达式为:
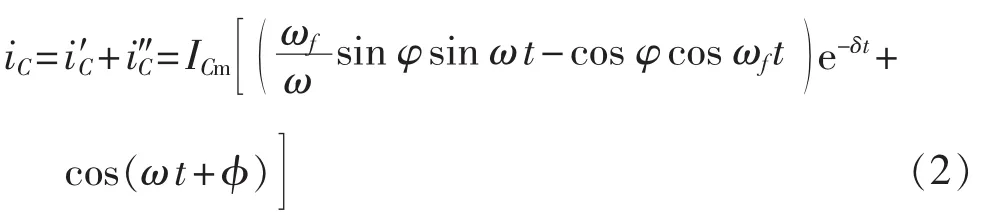
消弧线圈支路的暂态电感电流表达式为:
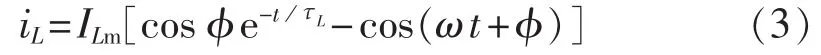
由上述暂态电容电流和暂态电感电流的分析可得,暂态接地故障电流id的数学表达式为:
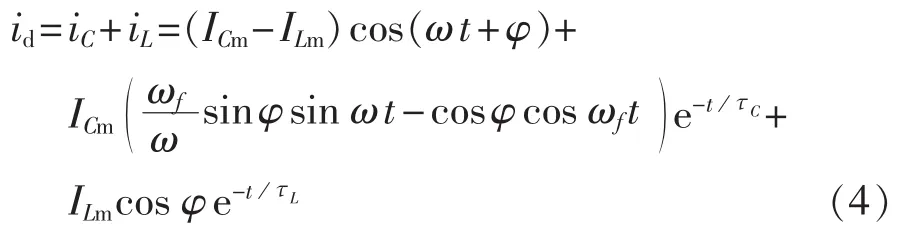
式(4)中第2个等号右侧第1项为接地故障电流稳态分量;其余为接地故障电流的暂态分量,等于电容电流的暂态自由振荡分量与电感电流的暂态直流分量之和。
经消弧线圈接地的配电网故障暂态零序电流的频率范围约为0~3000 Hz,在实际配电网络中馈线的零序阻抗远小于电容的容抗,可以忽略不计,单相接地故障时零序网络可以简化为图2所示[15]。
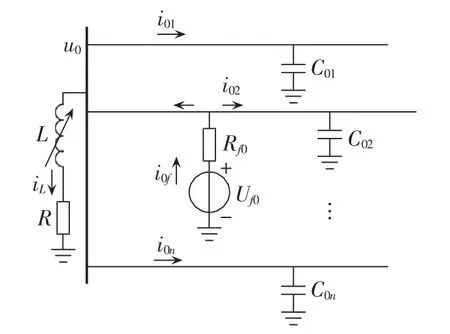
图2 单相接地故障零序网络简化图Fig.2 Simplified zero-sequence network for single-phase grounding fault
可简化得到故障馈线i零模电流、电压关系为:
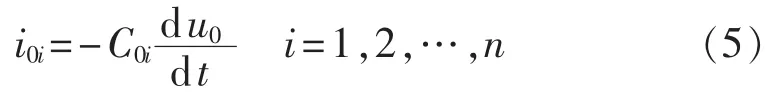
而对于健全馈线i零模电流、电压关系为:
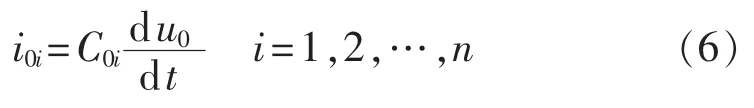
其中,i0i为流过线路i的零模电流;u0为母线零模电压;Uf0为故障点虚拟电源在零序网络上的压降;Rf0为零模过渡电阻;L为消弧线圈零模电感;R为消弧线圈串联零模电阻;C0i为第i条线路的零模分布电容。
从式(5)和式(6)可以看出,故障馈线的暂态零序电压导数与零序电流极性相反,健全馈线的暂态零序电压导数与零序电流极性则相同。暂态零序电流的幅值主要与馈线的零序分布电容相关。图3为小电流接地系统选线装置记录下的2次故障录波波形,其中图 3(a)为稳定型接地故障,图 3(b)为不稳定型接地故障,而实际中电缆线路的存在使得不稳定型故障常有发生。
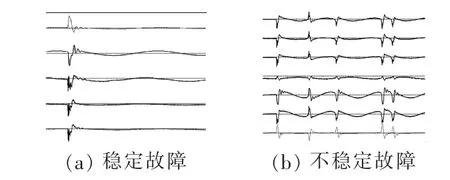
图3 配电网单相接地故障实测波形Fig.3 Measured waveforms of single-phase grounding fault in distribution system
2 单相接地故障暂态零序电流时频特征分析
配电网经消弧线圈接地系统发生单相接地故障后,量测端检测到的暂态零序电流分量是由不同频率分量构成的非线性、非平稳信号。小波包分解技术能够把任意信号映射到一个由小波伸缩而成的一组基函数上[16],信息量完整无缺,在通道范围内得到分布在不同频带的分解序列,更加清晰地刻画出故障暂态信号某频段的时频特性,可以为故障选线进行特征信息处理提供依据,所以利用小波包理论结合能量的观点,提高选线的准确性。
2.1 暂态零序电流时频特征量分析
当配电网系统发生单相接地故障时,对故障暂态零序电流按照适当的频带宽度采用小波包分解故障暂态信号采样序列,按照式(7)计算分解后各频带信号对应的幅值。

定义暂态零序电流时频特征量为:
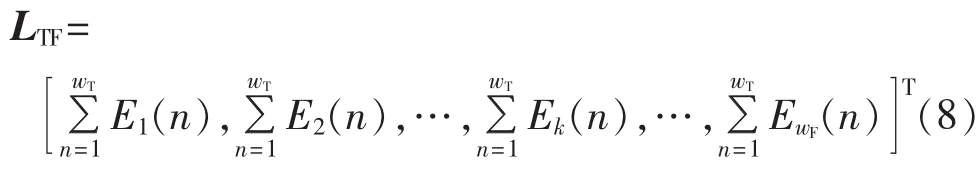
其中,wT和wF分别为时间窗和频率窗的长度。时频特征量能够较全面地反映暂态零序电流的时频变化特性。经消弧线圈接地配电网系统在相电压过峰值发生单相接地故障时,暂态零序电流主要是高频电容分量,暂态特征十分明显;当配电网在相电压过零点发生单相接地故障时,暂态零序电流主要是电感分量,暂态特征不明显,但是由于消弧线圈电感所引起的故障馈线衰减直流分量较大,健全馈线衰减直流分量较小,其只流过故障馈线而不流过健全馈线;当发生高阻接地故障时,暂态高频分量小,衰减速度快。综上,不同故障条件下暂态零序电流的时频特征分布则不相同。
利用时频相关系数来考察同一时频窗内不同馈线暂态零序电流的时频特征量的相似程度。设某2条馈线的暂态零序电流的时频特征量分别为LTF,x、LTF,y,其中 x、y为系统中任意 2条馈线,则可以定义 2条馈线之间的时频特征相关系数为:
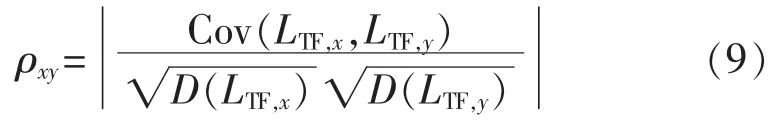
其中,Cov(LTF,x,LTF,y)为时频特征量 LTF,x、LTF,y的协方差,为时频特征量的均方差,其中ρxy的取值为0~1,当2条馈线之间的时频特征量越相似,即2条馈线的暂态零序电流的时频分布越接近,则 ρ值越大[17]。
2.2 暂态零序电流时频特征分布
建立110 kV/35 kV配电网单相接地故障模型如图4所示,Z型变压器中性点通过消弧线圈串联电阻接地。架空馈线l1=15 km,l3=18 km,l5=30 km;线-缆混合馈线l4=17 km,其中架空馈线12 km,电缆5 km;电缆馈线l2=6 km,l6=8 km。架空馈线为JS1杆型,LGJ-70型导线,档距为80 m,电缆馈线为YJV23-35/95 型电缆。

图4 配电网谐振接地系统Fig.4 Resonantly earthed distribution system
该电网中的G为无限大电源;T为主变压器,Yn/d11接线,变比为 110 kV/35 kV;TZ是 Z 型变压器;L为消弧线圈电感值;R为消弧线圈的阻尼电阻。馈线采用架空线路、架空线-电缆混合线路和电缆线路3种线路。
设图4所示配网的电缆馈线L2距离母线3 km处发生AG故障,故障初始相角为90°,故障过渡电阻为20 Ω时,采样频率为10 kHz,仿真一次侧检测到故障馈线L2及健全馈线L4的零序电流如图5所示。
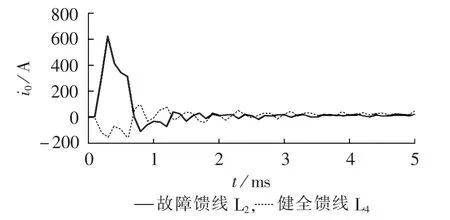
图5 故障初始相角为90°时的零序电流Fig.5 Zero-sequence current when initial fault angle is 90°
当故障初始相角为90°时,故障暂态特征明显,暂态零序电流主要是高频电容分量,健全馈线与故障馈线零序电流波形相似度较低。利用小波包分析得到的健全馈线L4及故障馈线L2的零序电流时频特征分布如图6所示。
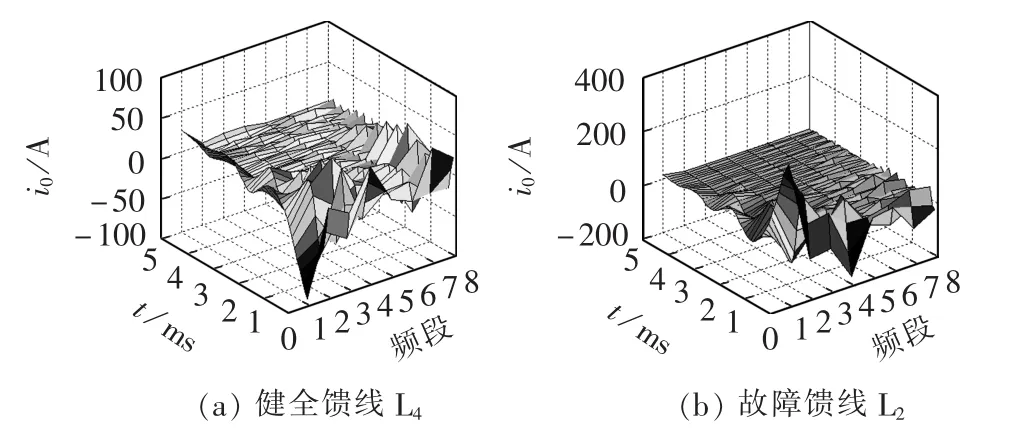
图6 零序电流时频特征分布Fig.6 Time-frequency distribution of zero-sequence current
一般配电网故障电弧的过渡电阻小于2 Ω,但是由于导线坠地、树木与架空馈线接触引起的高阻故障时有发生,尤其是当故障初始相角为0°时,使得常规的选线方法难以检测此类故障。设图3所示配网的电缆馈线L2距离母线3 km处发生AG故障,故障初始相角为0°,故障过渡电阻为1000 Ω时,采样频率为10 kHz,仿真一次侧检测到故障馈线L2及健全馈线L4的零序电流如图7所示。相对于低阻故障而言,高阻故障时暂态高频分量小,衰减速度快。
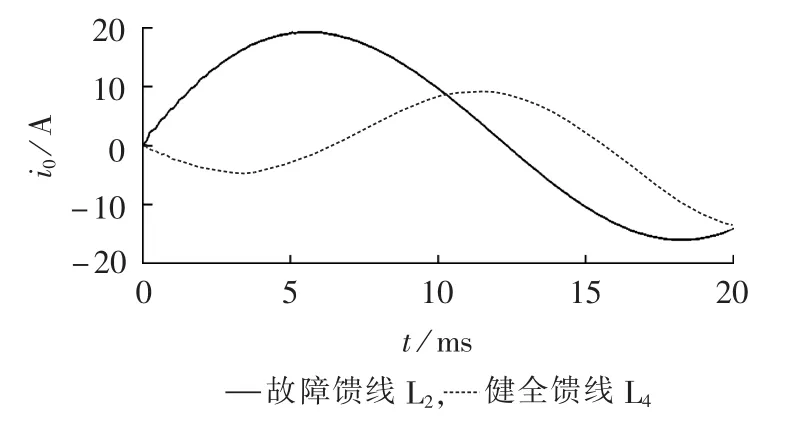
图7 故障初始相角为0°时的零序电流Fig.7 Zero-sequence current when initial fault angle is 0°
利用小波包分析得到的健全馈线L4及故障馈线L2的零序电流时频特征分布如图8所示。

图8 零序电流时频特征分布Fig.8 Time-frequency distribution of zero-sequence current
3 基于时频特征量的故障选线原理
前文理论与仿真分析表明,时频特征相关系数能够很好地表征各馈线暂态零序电流之间的时频特征分布相似度。但当系统出现不同条件下的单相接地故障时,可能会导致时频相关系数差别很小,故需要借助暂态零序电流时频能量观点更加完整、全面地描述各馈线零序电流的时频特性差异。定义时频特征相似度为:
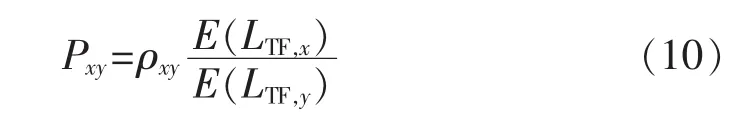
其中,E(LTF,x)和 E(LTF,y)为时频特征量的期望,Pxy表征2条馈线暂态电流行波时频特征的总体分布相似度。
用时频相似度Pxy进行故障选线的判定需要做多次判断。由时频相似度Pxy求取每条线路相对于其他线路的综合相关系数 ρli(i=1,2,…,n),利用 ρli形成直观简便的故障选线判据,加剧了故障馈线与健全馈线之间的差异性,同时提高了选线裕度。定义馈线 i的综合相关系数[18]为:
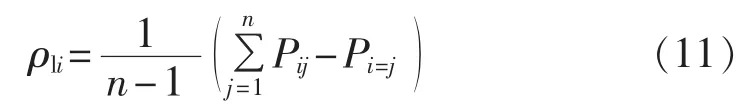
基于上述选线原理,经中性点消弧线圈配电网接地故障时,分3个步骤实现故障选线。
a.当零序电压超过门槛值时,选取5 ms的暂态零序电流数据利用db10进行3层小波包分解重构,计算其时频特征量。
b.求取时频相关系数,然后构造时频相似度并求取各条馈线综合相关系数。
c.将综合相关系数ρli最大的前3个按照大小排序为:ρla、ρlb、ρlc,当满足 ρla>ρlb+ρlc时,判断 ρla对应的馈线为故障馈线,否则,判断为母线故障。具体选线流程如图9所示。
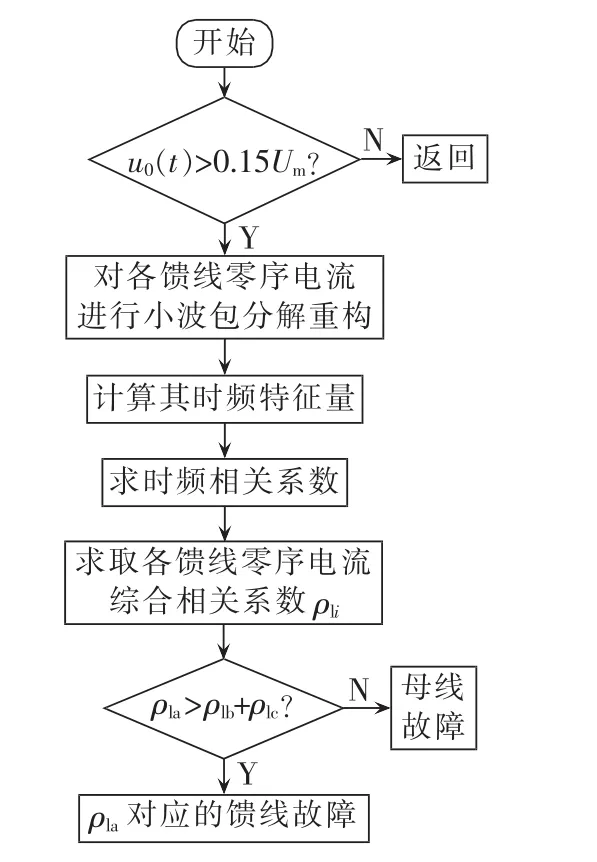
图9 故障选线算法流程图Fig.9 Flowchart of faulty line selection algorithm
4 仿真验证与适应性分析
采用本文所述的选线方法,图4所示配电网系统距离馈线L2始端3 km处发生AG单相接地故障,接地电阻50 Ω,故障初始相角90°,采样频率 10 kHz。从故障后选取5 ms的暂态零序电流数据,利用db10进行3层小波包分解重构,求取各馈线的时频特征量LTF和时频特征相似度矩阵,形成综合相关系数矩阵Pij:

综合相关系数最大的前3个按照大小顺序排列分别为:P2=172.1959,P6=126.1762,P5=10.5826,因此,P2>P5+P6成立,P2对应的馈线L2为故障馈线。由此可见,基于暂态电流时频特征量能正确进行选线。限于篇幅,本文只列出部分结果,如表1所示。
考虑选线算法在实际应用中可能存在的影响因素,仿真验证在以下不同故障情况下能实现正确选线。
4.1 电弧故障
馈线L2在距母线4 km处发生电弧故障的选线结果如表2所示。

表1 故障选线结果Tab.1 Results of faulty line selection
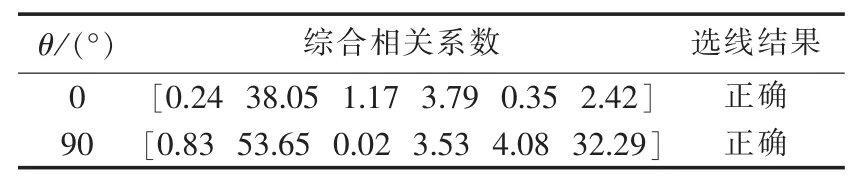
表2 馈线L2电弧故障的选线结果Tab.2 Results of arc-grounding fault in line L2
4.2 缆-线混合馈线故障
当缆-线混合馈线发生小角度故障时候,故障暂态分量小,故障信号难以检测。图3所示系统距离馈线L4始端4 km处发生AG单相接地故障,故障初始角为0°,过渡电阻10 Ω,利用本文所述方法得到各馈线的综合相关系数为:[0.297 3 5.602 9 0.408 4 16.9188 0.7945 7.6200],P4>P2+P6成立,馈线 L4为故障线路。
5 结语
本文提出一种基于暂态零序电流时频特征量的配电网单相接地故障选线,从零序电流的时域和频域分析入手,利用小波包分解与重构更好地刻画了故障馈线与健全馈线的时频特征差异性。该方法能够有效克服缆-线混合馈线小故障角时暂态分量小的特点。同时发生短线路接地故障时,能避免非故障长线路电容电流的影响,实现正确选线。
