基于灰色傅里叶变换残差修正的电力负荷预测模型

黄元生，方 伟

（华北电力大学 经济管理系，河北 保定 071000）

0 引言

只有保证电能供需的平衡，才能有效地保证电网安全稳定运行，而电力负荷预测是保证电力供需平衡的重要前提，因此，合理的电力负荷预测是保证电网安全稳定运行的重要技术。当前电力负荷预测方法主要有传统的回归模型［1］、时间序列模型［2-3］和智能的人工神经网络模型［4-5］、小波分析模型［6］、模糊逻辑模型［7-8］、支持向量机预测模型［9-10］等。

电力负荷影响因素较多且难以分析各种因素对负荷特性的影响程度。各种电力负荷预测方法都存在各自的优缺点，其中，人工神经网络以其自适应、自学习、高容错能力等优点，在电力负荷预测建模中得到广泛应用并取得了很好的效果，但该方法存在易陷入局部极小、收敛速度慢等缺点，限制了其进一步应用。传统的时间系列法运算量较小、运算速度较快，但预测误差较大且不具备自适应学习能力。传统的灰色系统理论主要解决少数据、小样本、信息不完全和经验缺乏的不确定性问题［11-12］，但存在着预测精度不高，误差趋势增大等缺点。

在时间系列预测模型中，运用了很多误差改进方法，如灰色马尔可夫模型［13］，该模型在灰色 GM（1，1）模型预测的基础上，利用残差进行二次灰色预测并建立状态转移概率矩阵确定残差符号，得到最后的预测结果。该模型假设残差值都是按照固定的状态转移矩阵延展，缺少动态性。

基于以上分析，本文在灰色GM（1，1）模型预测的基础上，提出傅里叶变换残差修正模型。傅里叶变换是一系列不同频率正弦波的无限叠加，可提取出频率成分。将残差作为一个能量有限的时间系列，运用傅里叶变换强大的降噪音能力，提取出残差中反映负荷本质的信息。因此，理论上运用傅里叶变换对残差进行改进具有可行性。算例结果表明，灰色傅里叶变换预测精度相比单一的灰色预测和灰色马尔可夫预测有所提高。

1 GM（1，1）模型［14-15］

由于负荷数据是多种因素共同影响的结果，因此，有必要对历史数据进行预处理，过滤掉历史数列中异常值的干扰，本文采用滑动平均法减弱异常值的影响。

设原始数列 x′（0）=［x′（0）（1），x′（0）（2），…，x′（0）（n）］，滑动平均值计算公式为：

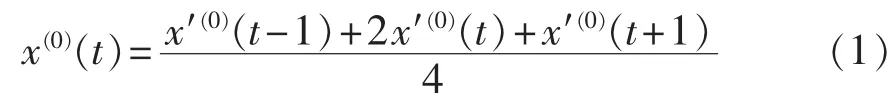
该数据既增加了当年数据的权重，又避免了数值过度波动。对于两端点的数据，计算公式为：

GM（1，1）模型是最常用的一种灰色模型，它由一个只包含单变量的一阶微分方程构成，是电力负荷预测的有效模型。经过预处理后的数据为：

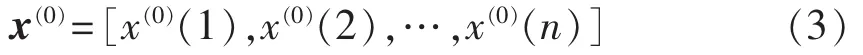
进行一次累加生成处理，得到：

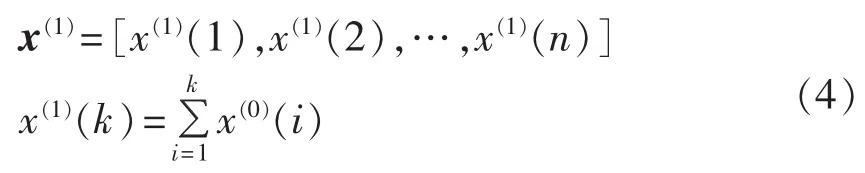
由于序列 x（1）（k）具有指数增长规律，而一阶微分方程的解恰是指数增长形式，因此可以认为序列x（1）满足下列一阶线性微分方程模型。

为求 a 与 u 的值，把式（1）离散化得到 x（0）（k+1）+取不同的 k 值得到：

简记为Yn=BA，且有：

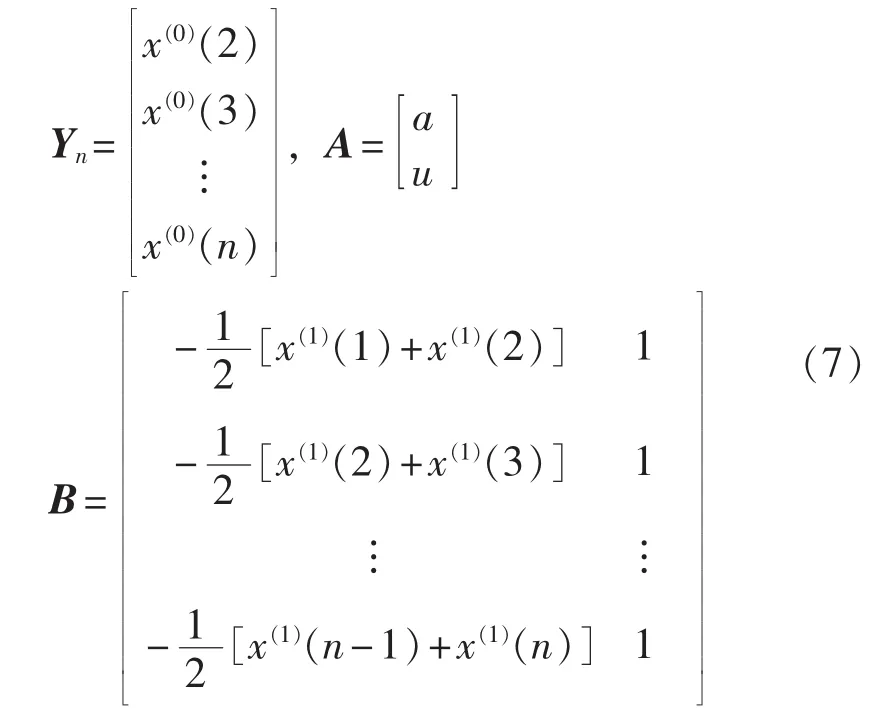
利用矩阵求导公式可得：

其中，k=0，1，2，…。

2 傅里叶变换残差修正模型

设f（x）是一个能量有限的模拟信号，则其傅里叶变换即为f（x）的频谱。因此将随机序列x的n个观测数据视为一能量有限的时间序列，对其作傅里叶变换得到观测数据的频谱，频谱的中心是低频段，外围是高频段，一般认为低频段是反映系统本质的信息，高频段反映的是系统数据的噪声。采集到的电力负荷时间序列数据一般都含有很大的噪声，作傅里叶变换可将其滤除，选择反映电力负荷本质的信息［16］。

鉴于傅里叶变换强大的降噪功能，运用傅里叶变换对灰色GM（1，1）的预测残差进行修正，能够滤除电力负荷时间序列数据中的噪声，从而提高了预测精度。下面介绍具体建模过程。

构建残差时间序列。由数据的就近原则，最近的数据反映电力负荷的本质，所以构建的残差时间序列如下：

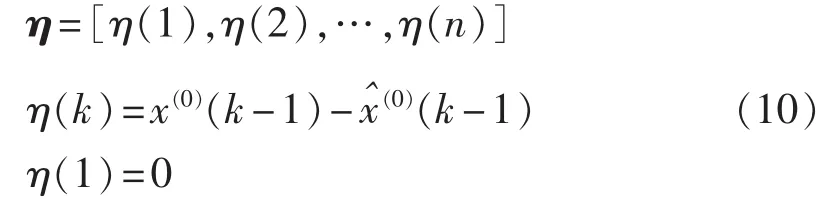
傅里叶变换残差表示为：

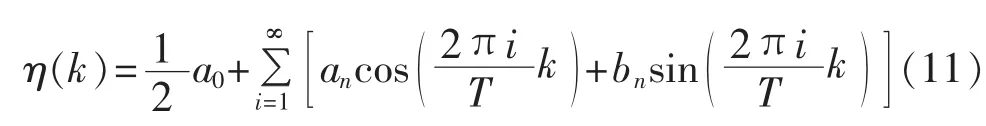
其中，k=2，3，…，n；T＝n-1。

把 η（1）=0 代入式（11），得到：

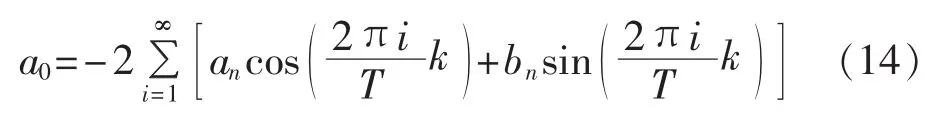
将电力负荷实际值代入式（12）—（14）求得 an、bn、a0，进而求得傅里叶变换残差序列η。

因此得到傅里叶变换残差改进的电力负荷预测值为：

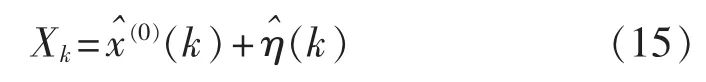
其中，Xk为最终预测值，为一般灰色 GM（1，1）预测值，为随机误差。

3 实证分析

本文选取某市从1997年到2004年8年的电力负荷值建立模型，该历史数据如表1所示。

表1 电力负荷历史数据Tab.1 Historic power load data

利用上述8年的历史数据建立模型，并以接下来4年的历史数据与预测值作比较，验证所建改进预测模型的有效性。

首先建立一般的GM（1，1）模型，利用滑动平均法对历史负荷数据进行预处理，得到处理后的负荷值为 x（0）=［118.4603，124.2508，134.2988，145.4745，157.355 3，168.613 3，177.976 3，184.449 0］MW，进行一次累加得到 x（1）=［118.4603，242.7110，377.0098，522.4843，679.8395，848.4528，1026.4290，1210.8780］MW。

由式（11）对i反复取值运算，使预测值更接近真实值，进而求得傅里叶变换残差（9）=-3.956MW。

最终得到2005年残差修正的电力负荷预测值为 X9=（0）（9）+（9）=201.385+（-3.956）=197.429（MW）。由2005年的真实值和预测值，得到 η（10）=196.35-197.429=-1.079（MW），求得同理求得（11）=3.973 MW，（12）=3.564 MW，进而得到X11=230.755 MW，X12=250.013 MW。

傅里叶变换GM（1，1）模型计算得到的结果与一般 GM（1，1）、马尔可夫 GM（1，1）模型计算得到的结果进行比较与分析，如表2所示。

表2 预测结果Tab.2 Forecasting results

由表2可知，傅里叶变换残差修正模型的预测值比一般 GM（1，1）模型和马尔可夫 GM（1，1）模型更接近于真实值，预测精度较高。

4 结论

a.在对样本值进行预处理时，运用滑动平均法滤除异常值的干扰，处理后的样本值对负荷的预测更科学、合理。

b.提出的基于傅里叶变换残差修正的电力负荷预测模型，克服了马尔可夫残差修正缺乏动态性的缺陷。

c.通过不同方法对同一样本值的预测可知，傅里叶残差修正模型与马尔可夫残差修正模型相比，其预测值与真实值的差距较小，预测精度有所提高，证明了该模型的有效性。