基于自适应陷波滤波器的谐波分析法

李功新 ，黄彦婕 ，江修波

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.福州大学 电气工程与自动化学院，福建 福州 350108；3.福建省电力有限公司，福建 福州 350000；4.福建省电力有限公司 厦门电业局，福建 厦门 361000）

0 引言

介质损失角（下文简称介损角）正切是衡量电气设备绝缘性能的重要指标［1］。在正常情况下，容性设备的介损角的范围为0.001～0.02 rad，是一个微小值，实际测量时容易因测试方法的不准确或现场干扰而淹没真实值。因此，研究高精度的介损角测量方法是介损角诊断绝缘性能研究的首要课题。

目前常用的数字化测量方法主要有谐波分析法、相关函数法、相位差法、过零时差法、正弦波参数法等［2-4］。其中相位函数法、过零时差法只能针对基波正弦信号，在实际应用中需前置滤波环节；正弦波参数法计算量大，而且在消除频率波动及噪声引起的误差方面不具备优势，较少采用［5］；谐波分析法不受直流分量和谐波存在的干扰，是目前较常用的方法，然而非同步采样时存在频谱泄漏和栅栏效应影响［6］。经进一步分析发现因频率波动而无法同步采样时，信号初相角差异和谐波是造成测量误差的主要因素［7］，同时传感器信号的长距离传输带来的随机噪声也必然影响着测量精度［8］。另外，电压、电流中可能存在的间谐波是谐波分析法无法滤除的误差。因此提高谐波分析法的测量精度需要：准确跟踪电压、电流频率，实现整周期采样；预先滤除电压、电流波形中的整次谐波、间谐波、直流和噪声干扰。

本文提出了结合自适应陷波滤波器（ANF）的谐波分析法，通过ANF滤除电压、电流信号中的整次谐波、间谐波、直流和噪声干扰，实现基波提取和频率跟踪［9］，并将提取的电压、电流基波波形和频率通过谐波分析法计算介损角，从而增加介损角的测量精度。最后通过仿真分析验证了改进算法的有效性。

1 基于ANF的基波提取和频率跟踪

介损角在线监测时电压、电流均包含着各次谐波分量、直流分量及噪声，以电压为例有如下形式：

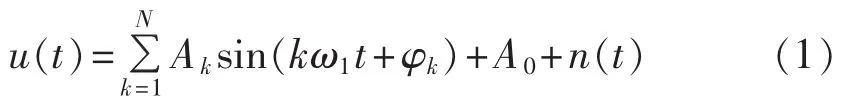
其中，Aksin（kω1t+φk）为各次谐波，k 为谐波次数，当k 取非整数时则表示该部分为间谐波；A0、n（t）分别对应着直流分量及噪声，采用ANF可以从中提取出基波分量和基波频率值［10-12］。

1.1 ANF的基本算法

ANF的数学表达式如式（2）所示：

当输入信号仅含基波分量，即 y（t）=A1sin（ω1t+φ1）时，ANF将有唯一解：

1.2 采用ANF提取基波和跟踪频率

为从包含整次谐波、间谐波、直流分量及噪声的电压、电流中提取基波分量及频率，对ANF的结构进行调整，以电压为例，ANF变换为式（4）：

将式（1）代入式（4），式（4）将有唯一解如下：

此时ξk、γ是决定ANF中第k次谐波分量及基波频率的收敛速度和精度的参数。x˙k/（kω1）是第 k次谐波分量的估计值，θ仍为基波角频率。理论分析可知，将式（4）中的k依次取采集电压所包含的各次谐波分量次数，并将k取不同值的多个公式联立，即得到求解基波及其频率的公式。实际应用中k的取值应根据所服务的电网情况而定，若电网中所含谐波情况较为复杂，则k可以取若干个含量较高的谐波分量次数。同理，当电流含有各次谐波分量及噪声时，上述方法同样可以实现基波分量的提取。

2 谐波分析法

谐波分析法利用三角函数的正交性，将采样信号与基波频率正余弦函数进行周期积分，从而获得基波分量的幅值和相位信息。当信号周期为采样周期整数倍时，谐波分析法利用矩形或梯形插值将积分离散化，当采样周期足够小时，可以获得准确度很高的拟合积分效果。然而，实际信号频率一直处于波动状态，因而多数情况下信号周期不为采样周期整数倍，此时需要对积分离散方法进行调整，从而保证基波信息提取的准确性。包含谐波分量及直流分量的电压、电流可表示如下：

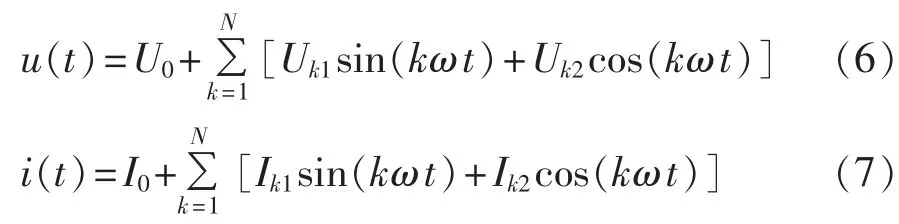
其中，等号右边第1项为直流分量，第2项为各次谐波分量。

以电压信号为例，其基波正、余弦分量分别如式（8）、（9）所示。

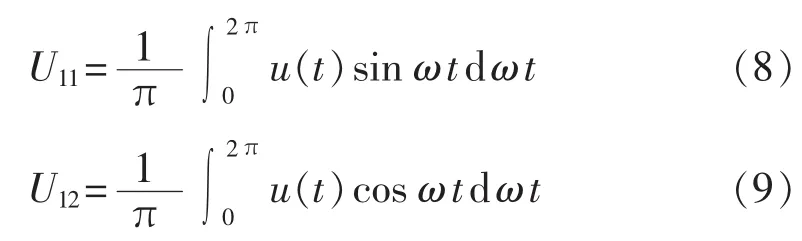
设实际信号周期T与采样周期Ts的关系为：

其中，L为整数，e为正小数。

基于梯形插值对式（8）、（9）离散化，并对非整采样周期部分进行估算，根据cos 2π=1、sin 2π=0，可得到如下结果：

其中，U（i）为电压信号在本计算周期内的第i个采样值，即 U（i）=u（iTs）；U′为 T 时刻的电压估计值，可利用式（12）所示的线性插值算法获得。根据相量夹角关系可计算出基波电压、电流的相位差φ，介损角δ为φ的余角，可由下式获得。

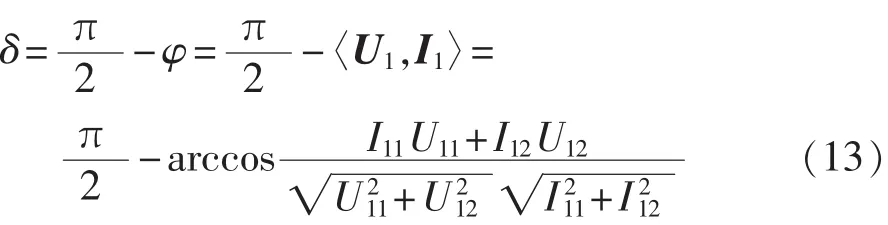
其中，U1、I1分别为基波电压、电流相量。

3 结合ANF的介损角测量

结合ANF和谐波分析法可得到计算介损角的新方法：通过ANF从采集的电压、电流信号中提取基波波形和基波频率，然后将所提取的分量代入谐波分析法进行计算，如图1所示。

图1 结合ANF的谐波分析法计算框图Fig.1 Block diagram of harmonic analysis based on ANF

4 仿真分析

为验证本算法的有效性，采用文献［13-14］中的试验电路参数及信号参数。电容型设备等效电路中C=591.02 nF，R=22.67 Ω。电压信号中包含基波、3次谐波、5次谐波，其表达式为：

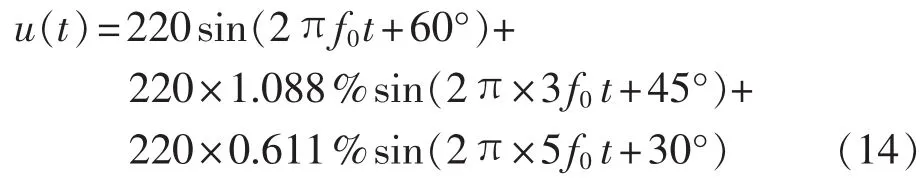
其中，基波频率f0=50 Hz。

4.1 信号基波提取及频率跟踪的仿真实验

在上述电压信号中添加能量为1%的随机白噪声作为 ANF 的输入 u（t），根据式（4）、（5）所列算法，提取基波信号 x˙1/ω1和基波频率 θ/（2π）。由于上述电压中仅存在基波及3、5次谐波，式（4）中的k依次取 1、3、5，即由 3 个式（4）所示的模块并联构成求解基波及其频率的算式，3个并联模块的参数设置分别为：γ=0.3，ξ1=1.1，ξ3=4，ξ5=7.5；采样频率 10 kHz。本算法仿真中，先将电压、电流幅值化归到接近1的数值后输入ANF，输出时再将信号同比例放大。在此后的介损角计算仿真中，仍对电压、电流信号做同样处理，从而减小因电压、电流幅值在数量级上的差异造成的数值计算误差。

提取的基波波形如图2所示，其中在0.1 s、0.2 s处分别设置了2次频率变换，使频率呈50Hz、50.5Hz、49.5 Hz的阶梯状。从图中可以看出，提取的基波除了在初始阶段与实际波形存在差异，在其他任意时刻都与实际波形准确地吻合。

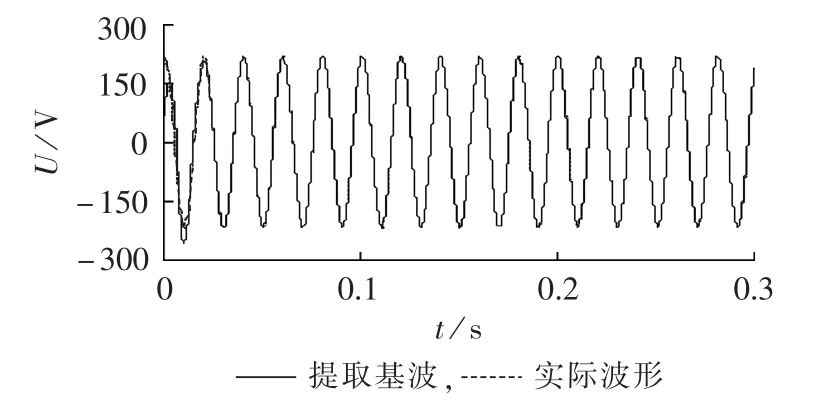
图2 电压基波提取波形Fig.2 Extracted fundamental voltage waveform

电压频率跟踪情况如图3所示，在频率突变时，该算法均能迅速跟踪到实际频率。频率由50 Hz变换到50.5Hz时，跟踪到误差小于0.1%，耗时0.039 s；频率由50.5 Hz变换到49.5 Hz时，跟踪到误差小于0.1%，耗时 0.049 s。

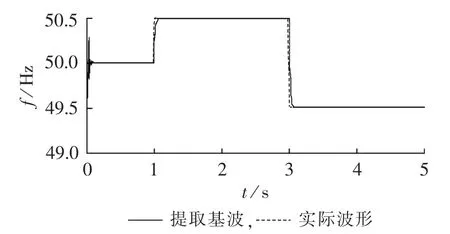
图3 电压频率跟踪波形Fig.3 Followed voltage frequency waveform

4.2 频率波动对介损角测量的影响

对本文所提出的介损角测量方法进行仿真，电网频率在49.8～50.2 Hz的范围内波动时，介损角测量误差见表 1［13，15］。相较于文献［15］中采用的基于Hanning窗的FFT介损角测量方法和文献［13］中基于三角自卷积窗（TSCW）的FFT测量方法，本文所采用的结合ANF的谐波分析法能够有效抑制频率波动对介损角测量的影响，其介损角测量相对误差小于0.003%，具有较高的介损角测量精度。

表1 频率波动对介损角测量的影响Tab.1 Influence of frequency fluctuation on dielectric loss angle measurement

4.3 谐波含量对介损角测量的影响

谐波含量越高对介损角测量的干扰越大，本文采用的算法针对该点预先消除谐波影响，提高介损角在线测量精度。将电压信号式（14）中3次谐波含量由0变动至8%，测量误差情况见表2。仿真中基波频率50.2 Hz，介损角真值0.004226 rad。如表2所示，相较于加 Blackman-Harris窗的谐波分析法［14］和基于TSCW的FFT测量方法［13］，结合ANF的谐波分析法能够有效抑制谐波对介损角测量的影响，实现介损角的准确测量。由于ANF消除整次谐波和间谐波的原理相同，因而本文算法在间谐波影响下同样能实现介损角的准确测量。

表2 谐波含量对介损角测量的影响Tab.2 Influence of harmonic content on dielectric loss angle measurement

4.4 介损角真值变化时测量的准确度分析

介损角越小对算法的准确度要求越高。实际介损角的变化范围为0.001～0.02 rad，从中间隔选取不同的介损值进行仿真，测量误差情况如表3［14］所示。介损角真值在上述范围变化时，文献［14］采用的基于Blackman-Harris窗插值谐波分析法的误差标准差小于4.5×10-5rad，本文采用的算法测量误差绝对值小于2.3091×10-7rad，准确度提升了2个数量级。

表3 介损角真值变化对介损角测量的影响Tab.3 Influence of its actual value variation on dielectric loss angle measurement

4.5 信号初相角变化对介损角测量的影响

当频率波动无法整周期采样时，介损角测量误差会随信号初相角而变化。表4给出了电压初相角变化时，采用本文算法得到的介损角的测量误差，设置基波频率在50.2 Hz左右波动时，算法通过ANF自动跟踪基波频率。可见初相角变化时，本文算法的测量绝对误差均在10-7rad数量级，算法稳定性较高。

表4 初相角变化对介损角测量的影响Tab.4 Influence of initial phase angle on dielectric loss angle measurement

4.6 白噪声对介损角测量的影响

在电气量测量时，受电磁干扰等环境因素影响，不可避免地存在白噪声，白噪声严重时将淹没介损角的真实值。通过比较不同信噪比下介损角的测量误差，进一步论证算法的实用性，比较结果如表5所示。基于ANF的谐波分析法能有效抑制白噪声对介损角测量的干扰，当信噪比大于60 dB时，测量绝对误差保持或低于10-5rad数量级，相较于加Blackman-Harris窗的谐波分析法［14］减小了1个数量级。当信噪比大于40 dB时，相对误差小于3.1%，可见此时算法仍具有较高的计算精度。

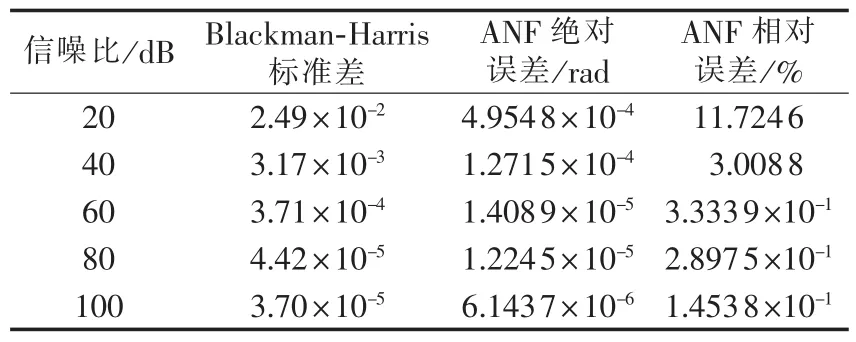
表5 白噪声对介损角测量的影响Tab.5 Influence of white noise on dielectric loss angle measurement

5 结论

经过仿真校验，本文所述方法的测量精确度较于以往的一些研究有所改进，仿真结果表明ANF能有效滤除电压、电流波形中的谐波和噪声分量，准确实现基波分量的跟踪及基波频率的提取，为改进传统谐波分析法测量介损角提供了有效的途径；结合ANF的谐波分析法在抑制频率波动、谐波干扰、噪声干扰等方面取得了明显的效果，在测量精度上较于以往的一些方法提高了1～2个数量级。