局部均值分解在电力系统间谐波和谐波失真信号检测中的应用

黄传金，曹文思，陈铁军，邱道尹

（1.中州大学 工程技术学院，河南 郑州 450044；2.华北水利水电大学 电力学院，河南 郑州 450045；3.郑州大学 电气工程学院，河南 郑州 450001）

0 引言

近年来，电力系统中的电能质量扰动信号检测成为研究的热点［1-7］，尤其是谐波扰动信号和间谐波信号检测备受关注［8-14］。快速傅里叶变换（FFT）不能处理非线性、非平稳的信号，在处理间谐波时还存在频谱泄漏和栅栏现象等缺点［15］。采用小波理论分析非线性、非平稳的信号有很大的局限性，一旦分解层数确定，其频率分辨率也就恒定，缺乏自适应，同时还受Heisenberg测不准原理的限制［16］。基于Hilbert-Huang变换（HHT）的电能质量检测方法虽取得了较好的效果，但在经验模态分解中采用三次样条插值拟合包络信号时易出现过包络、欠包络现象；HHT中过多的“筛分”次数导致端点效应污染整个数据段的程度较大，而且基于HHT的时频分析方法得到的瞬时频率常出现负值，这是难以解释的物理现象［17］。

2005年，Smith在前人研究的基础上提出了一种新的非线性、非平稳信号的分解方法——局部均值分解 LMD（Local Mean Decomposition）［18］。LMD 将复杂信号分解为若干乘积函数PF（Product Function）之和，每个PF分量由一个纯调频函数和一个包络函数之积组成，PF分量的频率可由纯调频函数直接求取，包络函数是PF分量的瞬时幅值。

LMD方法已成功应用于脑电信号的检测、瞬时频率信号的提取和机械故障诊断［17-20］。由于LMD避免了HHT中过包络、欠包络的现象，具有端点效应小，所求频率是正的、连续的、有物理意义的时变频率等优点，基于LMD的时频分析方法有望在电力系统故障检测与信号分析领域获得应用。

1 LMD

LMD本质上根据信号固有的包络特征自适应地将一个非线性、非平稳信号按频率递减的顺序逐级分离，得到若干个具有一定物理意义的PF分量，每个PF分量由纯包络信号和调频信号之积组成。以信号 x（t）为例，给出其分解步骤［19-20］。

a.找出信号x（t）的局部极值点 ni，任意 2个相邻的局部极值点平均值记为mi，则有：

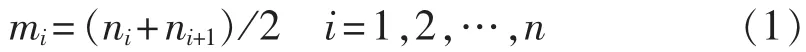
将式（1）中所有相邻的局部均值点mi和mi+1用折线连接，然后用滑动平均法对其进行平滑处理，得到局部均值函数 m11（t）。

b.求出包络估计值ai：

将式（2）中所有相邻的局部均值点ai和ai+1用折线连接，然后用滑动平均法对其进行平滑处理，得到包络估计函数 a11（t）。

c.将局部均值函数 m11（t）从原始信号 x（t）中分离出来，得到信号 h11（t）：

d.用 h11（t）除以包络估计函数 a11（t），得到调频信号 s11（t）：

对 s11（t）重复上述步骤，得到 s11（t）的包络估计函数 a12（t）。若 a12（t）不等于 1，说明 s11（t）不是一个纯调频信号，需要重复上述迭代过程n次，直至s1n（t）为一个纯调频信号，即 s1n（t）的包络估计函数a1（n+1）（t）=1，所以有：

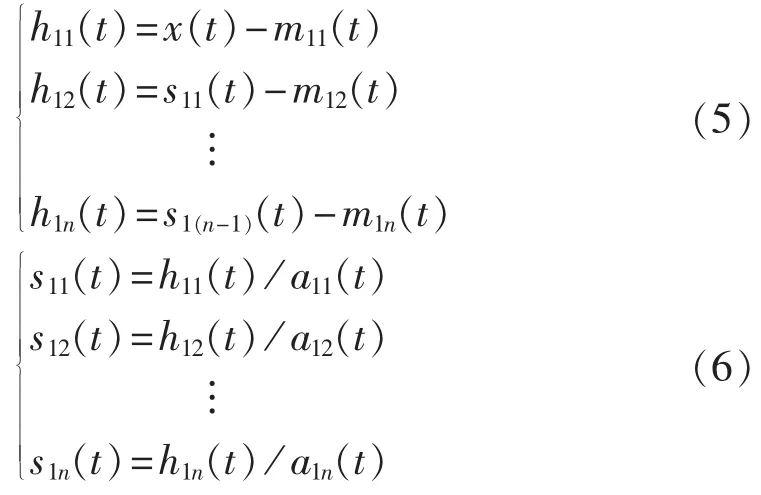
迭代终止的条件为：

实际应用中，为避免过多分解次数，设一个变动量 Δ，可令 1-Δ≤a1n（t）≤1+Δ 时，迭代终止。

e.将迭代过程中产生的所有包络估计函数做乘积，得到包络信号 a1（t）：

f.将式（8）得到的包络信号 a1（t）与纯调频信号s1n（t）做乘积，得到原始信号 x（t）的第 1 个 PF 分量：

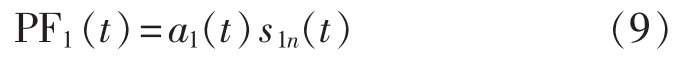
g.将 PF1（t）分量从原始信号 x（t）分离出来，得到信号 u1（t），将 u1（t）作为新的数据重复以上步骤，循环k次，直到uk（t）为单调函数为止。

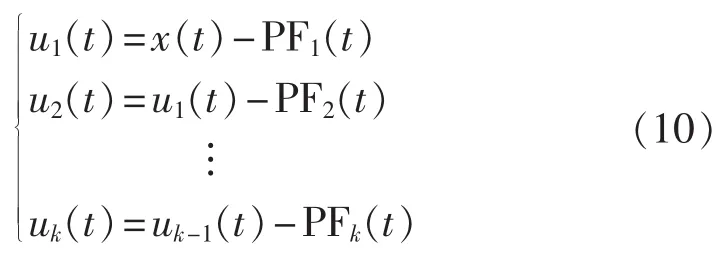
从以上步骤可以看出，原始信号可以由uk（t）和所有PF分量重构，即：

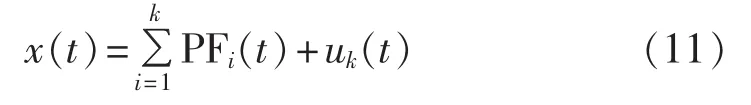
2 基于局部均值的瞬时频率求取

由式（11）可知信号可分解为若干PF分量之和，而每个PF分量由纯包络信号a（t）和纯调频函数s（t）=cos φ（t）组成，其频率 f可由纯调频函数 s（t）直接求解，即：

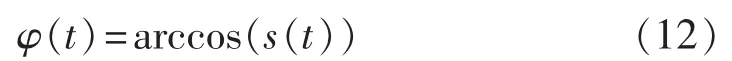
将式（12）展开并求导，则可以求出 s（t）的瞬时频率，即相应PF分量的瞬时频率。因为是通过对余弦函数求导得出PF的瞬时频率，所以要求s（t）值在 ±1之间，如果 s（t）值近似等于 ±1，则用 ±1代替。这种求取频率的方法直观而且简单，简称直接法。和采用HHT求取瞬时频率的方法相比，直接法求取的瞬时频率始终是正值，不会出现HHT中负频率的现象。

3 基于LMD的仿真与实例分析

3.1 间谐波信号

设间谐波信号如下：

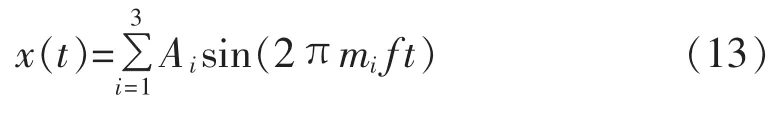
其中，A1=1 V，A2=0.3 V，A3=0.1 V；m1=1，m2=5.5，m3=11；f=50 Hz。

采样频率为6400 Hz，采样时长为0.4 s，变动量Δ=0.001，为验证LMD的优点，端点未作处理。运用LMD分离出的各PF分量和相应的纯调频函数如图1（a）所示，可知LMD按频率递减的顺序逐级分离出PF1、PF2和PF3分量；由纯调频函数求得的各PF分量的瞬时频率函数和采用HHT方法求取的瞬时频率函数如图1（b）所示；分别运用LMD和HHT求取的瞬时幅值函数如图 1（c）所示。由图 1（b）、（c）可知，用LMD分析间谐波时即使端点不作处理，分解得到的波形在端点处的效果可以与采用镜像拓延后的HHT方法相比拟；另外，这2种方法求取的瞬时频率和幅值都存在微小的波动，但根据LMD方法求取的瞬时特征参数的波动幅度明显较小。究其原因，一是LMD分解信号时采用平均滑动法拟合包络线，避免了HHT中采用三次插值时易出现过包络和欠包络现象，其端点效应较小；二是LMD通过除以包络均值函数得到PF分量，相对于HHT中采用减法的筛分过程，LMD得到一个PF分量时筛分次数较少，而筛分次数越少，端点效应向内污染的程度就越轻。

对HHT和LMD中所求瞬时参数波动问题，通常有2种方法：一种是取数据拟合后的稳态值作为检测值；另一种是将除端点部分的波峰值和波谷值相加，然后取平均值作为检测值。本算例采用最小二乘拟合，限于篇幅，本文仅显示了LMD所求间谐波频率f2的经数据拟合后的结果，如图1（d）所示。LMD、HHT经拟合后求取瞬时征参数以及加Blackman-Harries窗插值离散傅里叶算法求取的瞬时特征参数如表1所示。由表1可知，与HHT方法相比，LMD检测的频率和幅值准确性较高；与加窗FFT相比，用LMD方法获取的间谐波频率准确性略逊一筹，但就检测的幅值而言，LMD方法比加窗FFT方法的检测效果更好。

在装有Win7的神舟K480P-i5G笔记本（可用内存2.92 G）和MATLAB2011a仿真平台上，从分离原始信号直至获得信号的频率和幅值，LMD方法耗时1.148 769 s，HHT方法（HHT筛分停止条件采用Rilling 提出的准则［21］）运行了 2.203376 s，加窗 FFT花费了0.370305 s。与HHT相比，LMD方法的运行时间减少了1.054607 s。一方面，LMD筛分次数较少，另一方面，LMD通过对调频函数求导获得瞬时频率，而HHT方法求取信号的瞬时特征参数时需用Hilbert变换及其逆变换，所以HHT耗时较多。但与加窗FFT相比，LMD和HHT耗费的时间都较多。3种方法采样频率为6400 Hz。

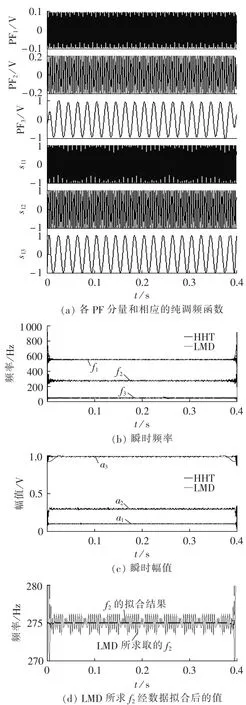
图1 间谐波信号分析结果Fig.1 Results of interharmonic signal analysis

表1 检测结果Tab.1 Results of detection

3.2 基于LMD的谐波失真信号分析［11］

为了和基于HHT的时频分析方法相对比，本文所取谐波失真信号和文献［11］中的前3个算例信号相类似。

3.2.1 短时谐波失真信号

设原始信号x（t）由基波信号和3次短时（0.08 s≤t≤0.2 s）谐波失真信号组成，基波信号的振幅为1 V，3次谐波信号的振幅为0.5 V；其波形如图2中的x（t）所示。采样频率为3200 Hz，运用LMD处理x（t）得到PF分量如图2中PF1、PF2所示；由LMD得到的PF分量按局部频率从高到低的顺序排列，故高频谐波信号在PF1分量中，由于PF分量由调幅函数和调频函数组成，故分析PF1分量可知基波和扰动谐波的幅值、频率以及扰动发生和恢复的时刻，PF1分量的幅值函数和瞬时频率分别如图2中的a1和f1所示。

图2 基于LMD的短时谐波信号分析Fig.2 Short-time harmonic signal analysis based on LMD

从图2中的PF1分量可以看出在0.08～0.2 s时段内的信号成分是扰动的谐波分量，其余时间的信号为基波分量；由PF2分量可知，在0.08～0.2 s时段内的信号成分是基波信号；图2中的a1和f1存在不同程度的波动，经数据拟合后得知，本文检测的基波信号幅值为0.9990 V，3次谐波幅值为0.4996 V，基波频率为50.07 Hz，3次短时谐波频率为150.01 Hz，另外，由瞬时频率函数f1还可知扰动信号发生时刻 0.08002 s，恢复时刻在0.2060 s。

和文献［11］采用HHT方法相比，LMD方法得到的瞬时频率更准确，而且求取的频率是正的、连续的、具有物理意义的时变频率，没有出现无法解释的负频率。

3.2.2 暂态谐波失真信号

图3中x（t）所示的暂态谐波失真信号表达式为：

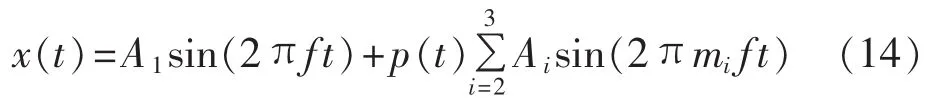
其中，当 0.12 s≤t≤0.24 s时 p（t）=1，其他时刻 p（t）=0；A1=1 V，A2=0.5 V，A3=0.3 V；m2=3，m3=7；f=50 Hz。采样频率为3200 Hz。用LMD求取的暂态谐波失真信号时频分析结果如图3所示。

图3 基于LMD的暂态谐波信号时频分析Fig.3 Transient harmonic signal time-frequency analysis based on LMD

从图3中的PF1和PF2分量可知，高次的谐波扰动分量包含在PF1分量中，低频次的谐波扰动信号在PF2分量中；由图3中PF1的瞬时频率函数f1可知高次谐波扰动发生时刻为0.1205 s，在0.2418 s恢复；由图3中PF2的瞬时频率函数f2知低频谐波扰动信号产生于0.1206 s，终止于0.2417 s。拟合PF1和PF2的瞬时特征函数可知高频扰动信号频率为349.7 Hz，振幅为0.2993 V；低频扰动信号的频率为150.1 Hz，振幅为0.4985 V。

从以上检测结果可知本文所提方法可准确确定多谐波扰动信号中每个谐波的频率、振幅和发生及恢复的时刻，并且频率没有发生突变，是正的、连续的、具有物理意义的时变频率。

3.3 时变谐波信号

时变谐波信号如图4中的x（t）所示。基波信号在0.12 s幅值从1 V骤升为2 V，在0.24 s幅值又骤降为1 V；在0.12 s加入幅值为1.6 V的3次谐波和幅值为1.2 V的7次谐波信号；0.24 s时3次谐波和7次谐波幅值分别骤降为0.8 V和0.6 V；时间长度为0.4 s，采样频率为3200 Hz，用LMD求取的时变谐波信号时频分析结果如图4所示。

图4 基于LMD的时变谐波信号分析结果Fig.4 Results of time-varying harmonic signal time-frequency analysis based on LMD

由图4中PF1和PF2可知在0.12～0.4 s时段，PF1分量对应7次谐波信号，PF2分量对应3次谐波信号。对图4中的中PF1的瞬时特征函数a1和f1进行数据拟合，可知7次谐波信号的幅值在0.12～0.24 s时段为 1.198 6 V，在0.24～0.4 s时段为0.6002 V；0.12～0.4 s时段检测的7次谐波频率为349.7 Hz。运用相同的方法，可知在0.12～0.4 s时段3次谐波信号的幅值为1.5994 V，0.24～0.4s时段为0.7992V；检测的3次谐波频率为149.8 Hz。从而可知，本文所提方法还可以确定多频谐波时变信号中每个时变信号的幅值、频率以及扰动发生和终止的时刻。

3.4 实例信号分析

某500 kV变电站采用电容式电压互感器对电压进行测量，电容式电压互感器二次侧装有谐振性阻尼器，35 kV母线分南母、北母2段。在进行35 kV南母电容器组投运操作时发生35 kV南母中间电压互感器高压保险B相熔断事故。图5给出了35 kV南母进行电容器组投切试验时采用尼高力波形记录仪（Nicolet vision）录取的35 kV侧B相电压暂态波形（采样频率为2 kHz，本文取最初的10个周期）及其对应的频谱图。基于LMD的时频分析结果如图6所示。

由图6（a）可知运用LMD可将35 kV侧B相电压分解为 PF1和 PF2分量；由图 6（b）中 PF1瞬时频率函数f1可以看出投切电容器前的频率为基波分量，投切后PF1的瞬时频率增大，为3次谐波成分，除端点外将波动的3次谐波频率函数的波峰值与波谷值相加求取的平均值为150.15 Hz，由此可知，运用LMD方法检测信号频率时有较高的精度；由PF2的瞬时频率函数f2可知电容器投切后B相电压有基波分量；从图6（c）PF1的瞬时幅值函数可知没有连接电容器时的基波幅值为30 kV，这与图5（a）中基波幅值很吻合，接入电容器后的3次谐波幅值较大，可知电容器投切后B相电压含有较多的3次谐波成分，而3次谐波成分较多是铁磁元件严重饱和的一个重要特征；另外，图6（c）从幅值曲线可以看出在投切电容器时引起了基波电压下降，这和理论情况相符，采用平均值法求取的电压下降后PF2的瞬时幅值为21.8 kV，可知基波电压从30 kV下降到21.8 kV；另外，从图 5（a）可知电容器在采样点 129（对应0.0645 s）时投运，从图 6（b）PF1的瞬时频率函数 f1可知在133采样点（对应0.0665 s）时产生了3次谐波，从图6（c）PF1的瞬时幅值函数也可知过132采样点（0.066 s）后的幅值在21.8 kV小范围内波动，由此可知，根据PF1瞬时频率f1或瞬时幅值函数可以确定基波下降的时刻和产生3次谐波的时刻。

另外，从图 6（b）可直观看出，与 HHT方法相比，本文所提方法求取的瞬时频率具有端点效应小、波动程度轻和更接近真实值等优点。

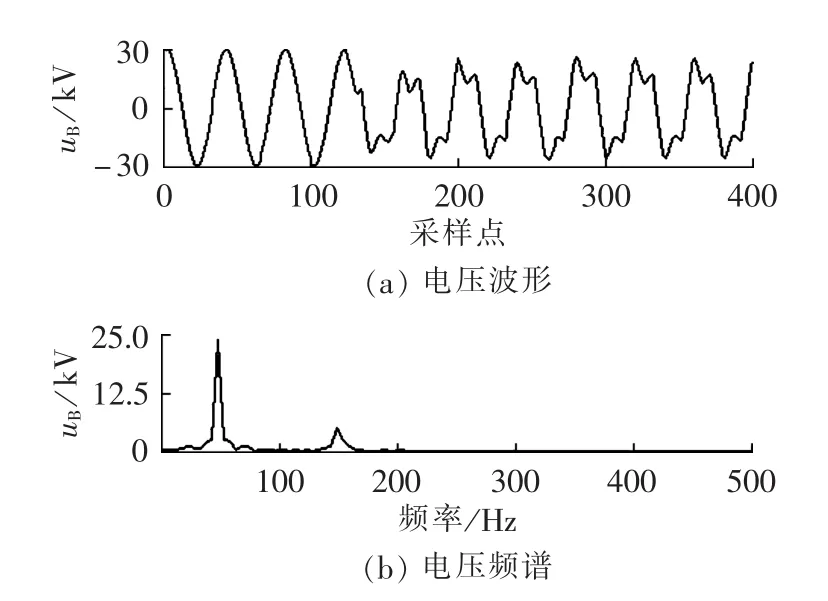
图5 35 kV侧B相电压波形及其频谱图Fig.5 Waveform of 35 kV-side phase-B voltage and its spectrum

图6 35 kV侧B相电压的LMD时频分析结果Fig.6 Results of time-frequency analysis based on LMD for 35 kV-side phase-B voltage

4 结论

本文首次利用LMD方法对间谐波信号、单频谐波信号、多频谐波信号、多频时变谐波信号和电容器组投运时的35 kV侧B相电压信号进行分析，从仿真及实验结果看出该方法可准确判断谐波扰动发生和恢复的时刻以及谐波信号的幅值和频率。间谐波信号仿真分析结果表明，与HHT相比，LMD方法具有运算量小、速度快、求取的瞬时特征参数波动幅度小、检测精度高等优点；从实际信号的频率分析对比结果可知，和HHT方法相比，本文所提方法具有很大的优越性。更重要的是用LMD方法所求取的瞬时频率都是正值，而且所得波形受端点效应的影响较小，为电力系统电能质量检测提供了一种新的途径。值得注意的是，作为一种新提出的非线性信号分析方法，LMD还有迭代终止条件、滑动平均跨度选取（本文取相邻极值点最长距离的1/3）和端点效应等理论问题需进一步研究。虽然LMD的端点效应较小，但谐波相位分析是建立在准确获取信号初值之上，导致该方法暂不能用于分析谐波相位。随着这些理论问题的解决，LMD将有良好的应用前景。