基于包含谐波模型的加权最小二乘估计算法的电压暂降检测方法

雷 何 ，高 山 ，林新春 ，康 勇 ，段余平 ，邱 军

（1.华中科技大学 强电磁工程与新技术国家重点实验室，湖北 武汉 430074；2.武汉钢铁（集团）公司，湖北 武汉 430083）

0 引言

电压暂降指电压有效值降至标称值的10%～90%的暂态过程，其持续时间一般是 0.01～60 s［1］。电压暂降产生的主要原因是电网中出现的短路故障及大容量负荷的启动等。由于计算机等敏感负载的日益增多，且这些设备对供电电压的变化比较敏感，因此电压暂降会使得这些设备工作异常，造成经济损失［2］。

动态电压恢复器能够有效保护敏感负载在电压暂降时不受其影响［3-5］。其原理就是在检测到电压暂降时，通过串联耦合变压器注入电压，维持敏感负载供电电压的稳定。因此，如何能够快速检测出电压暂降便成为一个国内外研究的热点问题。

常见的三相暂降检测方法有dq变换、αβ变换、pqr变换，其算法简单，较易实现，但检测速度受谐波影响较大［6］。而且电网中发生的短路故障并不全是对称的，其中单相短路故障占大多数［7-8］，因此三相检测方法的适用范围受到限制。基于1/8周期傅里叶变换检测法［9］、考虑相位跳变的检测法［10］等单相检测方法虽然在电压发生相位跳变时也能有较快的检测速度，但依然需要低通滤波器来抑制谐波的影响，若电网中谐波分量较大，需减小低通滤波器的带宽，增加了检测时间。基于离散傅里叶变换（DFT）来实时计算有效值的检测方法有比较好的滤波效果，但幅值收敛时间通常需要半个基波周期以上。基于改进DFT的检测方法缩短了检测时间，但相位跳变会影响其检测速度［11］。基于高阶卡尔曼滤波器的检测方法对谐波有较强的抑制，但检测速度不够理想。

本文提出的包含谐波模型的加权最小二乘估计WLSE（Weighted Least-Squares Estimation）算法适用于单相电压暂降检测，因此不受电网不平衡的影响，并且在电网电压含有大量谐波分量时也可以准确计算出基波和各次谐波分量，在电网电压发生暂降时，WLSE算法会重置协方差，该算法估算出的电压可以以较快的速度和较高的精度重新跟踪上暂降后的实际电压。由于频繁的重置协方差反而会降低电压暂降检测速度，因此，需要设置一个阈值来确保协方差在电网电压稳态时不会重置，而在电压发生一定深度的暂降时才会重置以提高检测速度。该阈值一般设置为大于电压实际采样值和估计值的稳态误差。在电网电压谐波分量较高时，相对于仅包含基波模型的WLSE算法［12］，包含谐波模型的WLSE算法的误差比较小，因此重置协方差的阈值可以设置得比较小。在电压暂降深度较小时，本文提出的算法有效避免了仅包含基波模型的WLSE算法因无法重置协方差而减慢检测速度的缺陷，并针对影响检测性能的几个实验条件分别对算法进行了实验验证。

1 包含谐波模型的WLSE算法

含N次谐波分量的单相电网电压Us的表达式为：

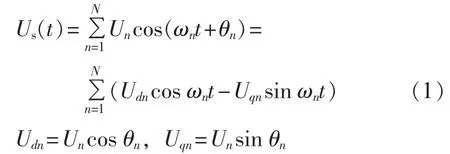
其中，Un、ωn、θn分别为单相电网电压中对应的基波和各次谐波分量的幅值、角频率及起始相角。

将等式（1）写成矩阵的形式，其表达式为：

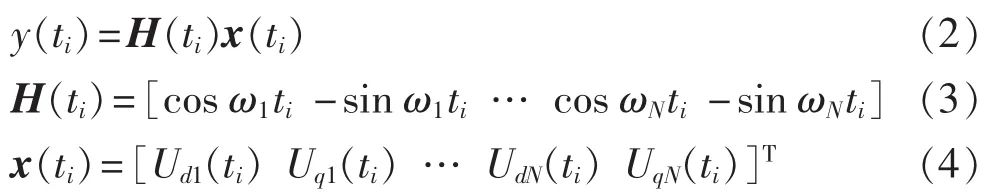
代价函数的表达式为：

WLSE算法的目的是为了最小化代价函数以达到最优收敛过程。由于对单相电网电压建立了N次谐波模型，因此需要准确估计基波及各次谐波分量，即需要对基波及各次谐波分量分别进行WLSE算法才能实现最优收敛。WLSE算法表达式为［13］：

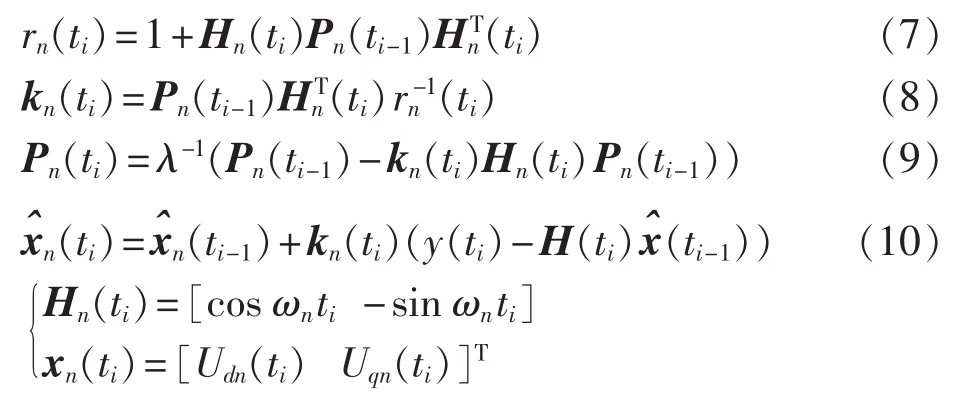
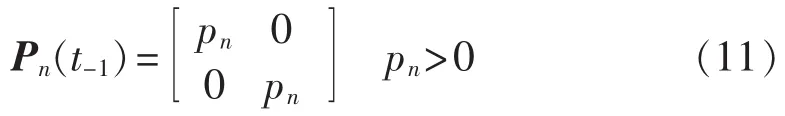
其中，pn为初始变量。

2 电压暂降检测

当电网电压发生暂降时，WLSE算法可能需要几个基波周期才能跟踪上暂降后的电压，这显然无法满足动态电压恢复器等电力设备对于检测时间的要求。为了能够更加快速地检测出电网的暂降，需要在WLSE算法中重置协方差，即将二维协方差矩阵Pn（ti-1）重置为初始值 pnI（I为二维单位矩阵）。而协方差重置的条件取决于WLSE算法的误差大小。

WLSE算法的误差可以由实际采样值与估计值之差得到：

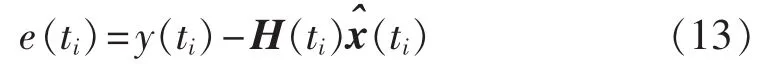
一般比较常见的是仅建立基波模型来进行WLSE算法，该建模方法在电网谐波较小时可以有较高的检测精度和较快的检测速度。但是当电网谐波较大时，由于仅包含基波模型的WLSE算法只估算基波分量，因此e（ti）中会包含较大的谐波分量。为了避免稳态时因频繁重置协方差而造成算法异常，因此需要设置阈值ε大于谐波分量幅值。而电网的谐波分量大小并不是恒定不变的，需要将阈值ε设定得较大来保证算法稳定。但是在电网电压发生小的暂降时，仅包含基波模型的WLSE算法无法重置协方差，会减慢检测的速度。

为了克服上述缺陷，本文提出了包含谐波模型的WLSE算法。该算法不仅可以准确估计电网基波分量，也可以准确估计谐波分量。因而在电网谐波较大时，相对仅有基波模型的WLSE算法，阈值ε可以设定为一个较小的值，在电压暂降深度较小时也能保证检测的快速性，提高了该算法对于电网电压暂降的检测性能。

由于较小的阈值容易造成算法在收敛过程中反复重置协方差，因此本文加入了延迟算法以增强算法的可靠性。当检测到误差超过阈值时会重置协方差，同时启动延时计数程序，在延时期间即使再次检测到误差超过阈值也不会重置协方差，只有延时结束后才能再次重置协方差。一般半个基波周期内电网电压连续发生2次暂降的情况极少出现，因此将延迟时间设置为半个基波周期。包含谐波模型的WLSE算法流程图如图1所示。

图1 包含谐波模型WLSE算法流程图Fig.1 Flowchart of WLSE algorithm with harmonic models

3 实验分析

由于电网中的高次谐波分量容易被低通滤波器滤除，因此对WLSE算法影响最大的是一些低次谐波分量。由于电网中偶次谐波分量较小，因此本文仅考虑奇次谐波。由于建立过多的谐波模型会使得各次谐波分量在收敛过程中互相影响，反而会减慢基波分量的收敛速度，增加检测时间，而且一般电网中3、5、7次谐波分量相对比较大，因此本文实验分析了包含3、5、7次谐波模型的WLSE算法。由于过小的阈值ε使得WLSE算法更容易受到噪声的干扰，因此本文将阈值ε设定为0.12U1。由于谐波分量相对于基波分量偏小，因此谐波分量的协方差可以设置得小一些，其表达式为：

本文在基于DSP2812控制系统的实验台架上进行实验分析，采样频率为5 kHz。并且将需要观测的变量转换为5 kHz的高频PWM信号，然后通过带宽为500 Hz的低通滤波器滤除高频分量，这样就可以将变量直观地显示于示波器上。

3.1 谐波抑制

为了验证本文提出的算法在谐波分量较大时也有良好的检测性能，利用可编程交流电源输出基波幅值为100 V、频率为50 Hz的单相电压，并且含有5%的3次谐波、5%的5次谐波、5%的7次谐波、2%的9次谐波、2%的11次谐波以及2%的13次谐波，以此作为暂降前的稳态电压，其表达式为：

其中，ω为基波分量的角频率。

由于包含谐波模型的WLSE算法估计的基波分量、各次谐波分量以及误差是程序内部变量，需要先将其转换为高频信号，利用低通滤波器滤除高频分量后显示到示波器上，其量程与实际采样电压不同。因此，为了便于分析，本文对基波分量、各次谐波分量以及误差的量程进行比例换算，使其与实际采样电压的量程保持一致。由于低通滤波器具有延时特性，因此在示波器上显示的估计值与实际的估计值相比会有一定的延时。

3.2 暂降检测

除了谐波对于暂降检测有较大的影响，暂降起始相位、暂降深度以及暂降时伴随的相位跳变也都会影响暂降检测的速度，因此需要设置不同的实验条件来验证本文提出的算法具有良好的检测性能，如表1所示。

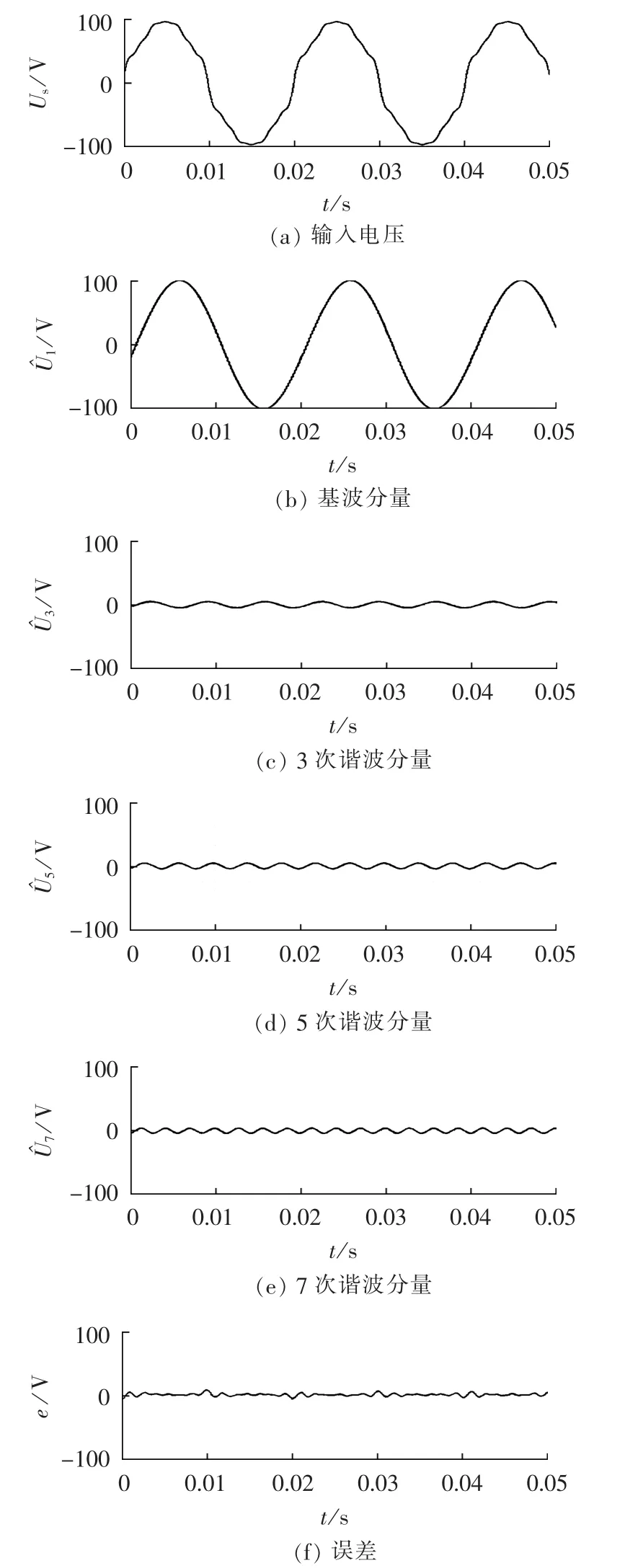
图2 包含低次谐波模型WLSE算法的稳态性能Fig.2 Steady-state performance of WLSE algorithm with low-order harmonic models

表1 不同的实验条件Tab.1 Different experimental conditions

起始相位为0°，即输入电压在0.1 s时发生暂降；起始相位为90°，即输入电压在0.105 s时发生暂降。

暂降后的电压表达式为：

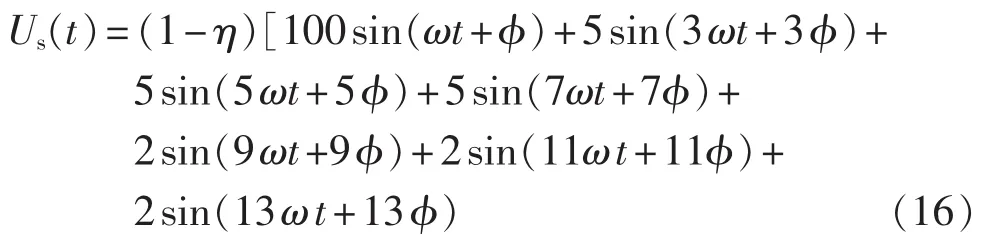
其中，η为暂降深度，φ为相位跳变角度。

图3给出了包含谐波模型的WLSE算法计算出的基波幅值在不同实验条件下的暂态过程，图中1为标幺值。在此，将检测时间定义为暂降后基波幅值低于90%额定值时所需时间，将稳定时间定义为暂降后基波幅值的误差稳定在±3%以内所需时间。

根据图3所得到的不同类型的暂降的检测时间和稳定时间如表2所示。

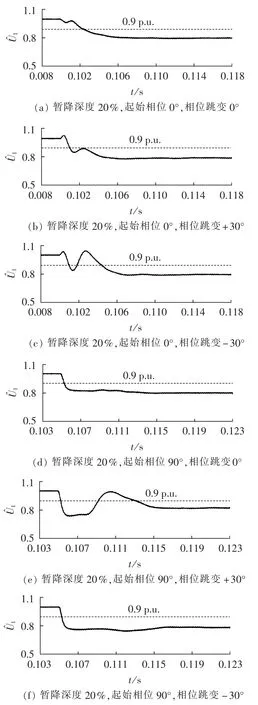
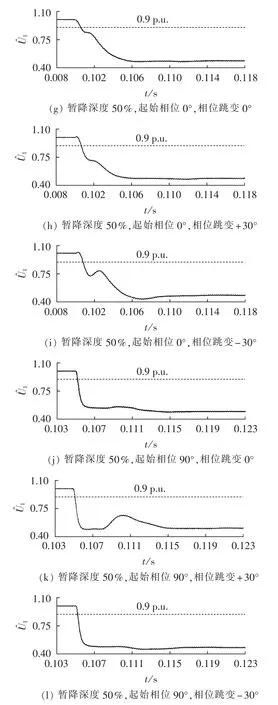
图3 基波幅值在不同类型的电压暂降时的暂态过程Fig.3 Transient process of fundamental amplitude for different types of voltage sag

从表2中可以发现，其他条件相同的情况下，起始相位为0°的暂降的检测时间均长于起始相位为90°的暂降的检测时间，但是稳定时间要短。原因在于0°暂降是在过零点处发生，需要等待误差逐渐变大才能重置协方差，而90°暂降是在峰值处发生，在暂降瞬间就立即重置协方差，因此90°暂降时基波幅值的响应时间相对较快，但是由于其误差突变相对较大，因而暂态过程的振荡时间相对较长。

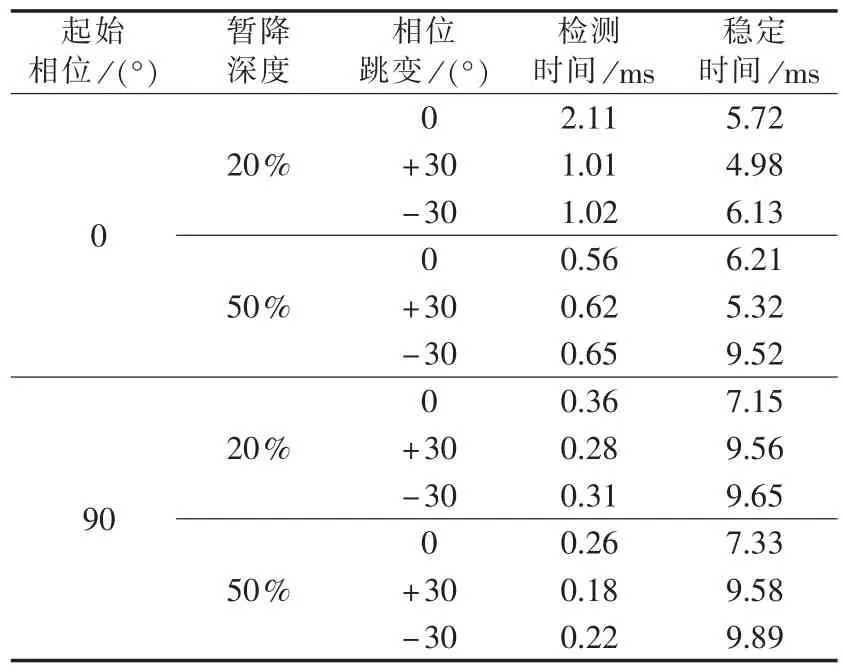
表2 不同的实验条件对方法的影响Tab.2 Impacts of different experimental conditions on method

其他条件相同的情况下，暂降深度的加大会减小检测时间，但是由于误差的变大，其稳定时间会增大。虽然如此，由于误差变化的暂态过程基本一致，因此暂降深度对于稳定时间的影响比起始相位小得多。

其他条件相同的情况下，电压暂降伴随相位跳变对检测时间的影响并不是很大，但是在起始相位为90°时对稳定时间的影响比较大，稳定时间比没有相位跳变的多2.5 ms左右。原因在于相位跳变使得误差更大，因此算法收敛需要更长的时间。

如图 3（b）、（c）、（e）所示，相位跳变会导致基波幅值的暂态过程出现较大振荡，在暂降深度较浅时，振荡容易使得算法误判断出暂降恢复。但是暂降一般都会持续半个基波周期以上，这里需要在暂降恢复判断程序中加入半个基波周期的延时判断即可。而且一般实际电网发生故障时，幅值暂降深度越大，相位跳变角度会越大。在幅值暂降深度较小时，相位跳变角度并不会很大，此时幅值的振荡幅度也会相对较小，因此该算法出现误判断的几率并不会很大。

4 结论

本文提出的包含谐波模型的WLSE算法由于加入了谐波模型，缩小了误差范围，即使在电网电压谐波较大时也可以将阈值ε设置得较小，因而在电压暂降深度较小时也可以及时重置协方差来保证算法的快速收敛。除了谐波，暂降起始相位、暂降深度及暂降时伴随的相位跳变都会影响检测性能。因此本文针对这些不同的实验条件，分别进行了实验分析。实验结果表明基波幅值降到额定值的90%所需时间为0.2～2ms，而基波幅值稳定所需时间则为5～10ms，验证了本文提出的算法具有良好的检测性能。