纽结带形建筑表皮的拓扑学分析

李滨泉

(浙江科技学院 建筑工程学院，杭州 310023)

纽结带形建筑表皮的拓扑学分析

李滨泉

(浙江科技学院 建筑工程学院，杭州 310023)

引进拓扑学的纽结理论来指导分析纽结带形表皮的设计，首先从分析纽结带形表皮的拓扑学特征入手，提出了纽结类带形表皮和链环类带形表皮设计的造型规律，同时利用琼斯多项式来阐述纽结带形表皮的拓扑同痕不变量，并分别对纽结带形表皮的复杂度，以及纽结带形表皮间的环绕、串联和拼合进行阐述，力求利用拓扑学中纽结理论解决一些建筑纽结带形表皮的设计中所遇到的问题。

拓扑学；纽结理论；拓扑同痕；纽结类带形表皮；链环类带形表皮；环绕

纽结是门古老而重要的学问。在没有文字以前，人类的祖先在史前时代就结绳来记事，《周易》中就有“上古结绳而治”的记载。数学中的纽结理论既直观又深奥，是拓扑学中引人入胜的一个分支。拓扑学是研究几何图形的连续变形的科学，纽结理论是研究空间闭合曲线(或多条空间闭合曲线)在连续变形下保持不变特性的理论[1]。

纽结带形建筑表皮作为三维空间中存在的具有形状、尺度、色彩和材质等因素的集合体，具有实用和观赏双重功能。但由于纽结带形表皮是表皮相互之间的跨越、互绕和环绕，导致纽结带形表皮形式多变，结构复杂，设计难度增大。随着建筑技术水平的提高，越来越多的建筑采用了复杂的纽结带形表皮的设计，但因缺乏系统的理论指导，其设计多局限于感性的层面上。因此，在理论的指导下进行理性的、系统的思考是必要的。本研究引进拓扑学的纽结理论来指导分析纽结带形表皮的设计，因为只有感性与理性有机结合的设计，才可能是日趋完美的设计[2-3]。

1 纽结(链环)类带形表皮的基本概念

从拓扑学理论看，结是三维空间中的与圆周同胚的曲线。虽然带形建筑表皮很少有完全闭合的，但应用拓扑学的纽结理论分析带形表皮的纽结时，带形表皮的宽窄、长短、曲直都不是设计人员所关注的，都允许改变，关键是对带形表皮的纽结规定。和一般建筑中的纽结不同，拓扑学研究的纽结一般是封闭的，没有能够自由活动的绳端，如果打了结的“表皮”两端没有连接起来，则结是可以“解开的”，所以在拓扑学里只讨论在闭合带形曲面上的结。带形表皮的端头不许抽回重穿，因为如果允许表皮端自由穿插，那么所有的结都能经过连续变形最后解开成一条笔直的表皮。于是建筑中非闭合纽结带形表皮可以规定表皮的两端先在远处捻合起来，成为闭合带形表皮，经过纽结理论分析研究后，再切断打开为非闭合纽结带形表皮，如图1所示。

图1 纽结带形表皮端头的闭合Fig.1 Closing for end point of knot-shaped skin

1.1 纽结的表皮分类

纽结的带形表皮分为纽结类带形表皮和链环类带形表皮两大类。纽结类带形表皮是三维空间中的简单带形闭曲面，简单带形闭曲面的意思是连通的(连成一体的)、封闭的(没有端点的)、不自交的(没有粘连的)曲面。平面内的圆形闭合带形表皮是一个特殊的“未打结的”纽结类带形表皮，称之为平凡纽结类带形表皮。最简单的不平凡的纽结是互为镜象对称的左手三叶结和右手三叶结，如图2所示。闭合带形表皮除了可以打结之外，表皮之间还可以互相勾连、套扣，这涉及链环类带形表皮的概念。由有限多条互不相交的简单带形闭曲面表皮构成的空间图形，称为链环类带形表皮，如图3展示了最简单的链环。组成链环类带形表皮的每一条简单带形闭曲面称为该链环类带形表皮的一个分支，它本身是可以有结的，这样纽结类带形表皮就成了链环类带形表皮的一种，是只有一个分支的链环类带形表皮。

1.2 纽结(链环)类带形表皮的拓扑同痕

如果一个纽结(链环)类闭合带形表皮(或一组闭合带形表皮)在空间中能通过伸缩和扭曲等自由地连续变形，但是不许切断，不许粘连，这种可以经过闭合带形表皮移位变形变成另一个纽结(链环)类带形表皮，这2个纽结(链环)类带形表皮就是同痕的。纽结(链环)类带形表皮理论的基本问题是：任给2个纽结(链环)类带形表皮，怎样识别它们是否同痕？打结的带形曲面和不打结的带形曲面是不同痕的。如图4(a)普通的双结“婆婆结”不能从所谓的图4(b)“海员结”得出，它很容易松开，所以它们是不同痕的。而图5给出的2种结的图形是同痕的。同痕不变量就是纽结(链环)类带形表皮在拓扑变形时不改变的性质。表皮投影图的分支数则是一个同痕不变量，因为3种基本变换都不改变它，换句话说，如果2个链环类带形表皮有不同的不变量，它们就一定不同痕。表皮纽结理论研究的主要目的就是寻求具有很强的鉴别力的同痕不变量。因此，同痕的链环类带形表皮应当具有相同的拓扑不变量。

图2 左手三叶结和右手三叶结Fig.2 Left trefoil knot and right trefoil knot

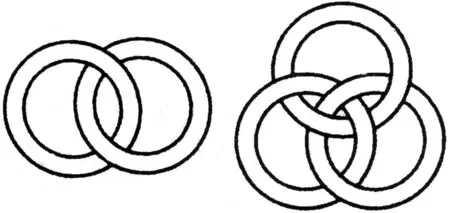
图3 最简单的链环Fig.3 The most simple link

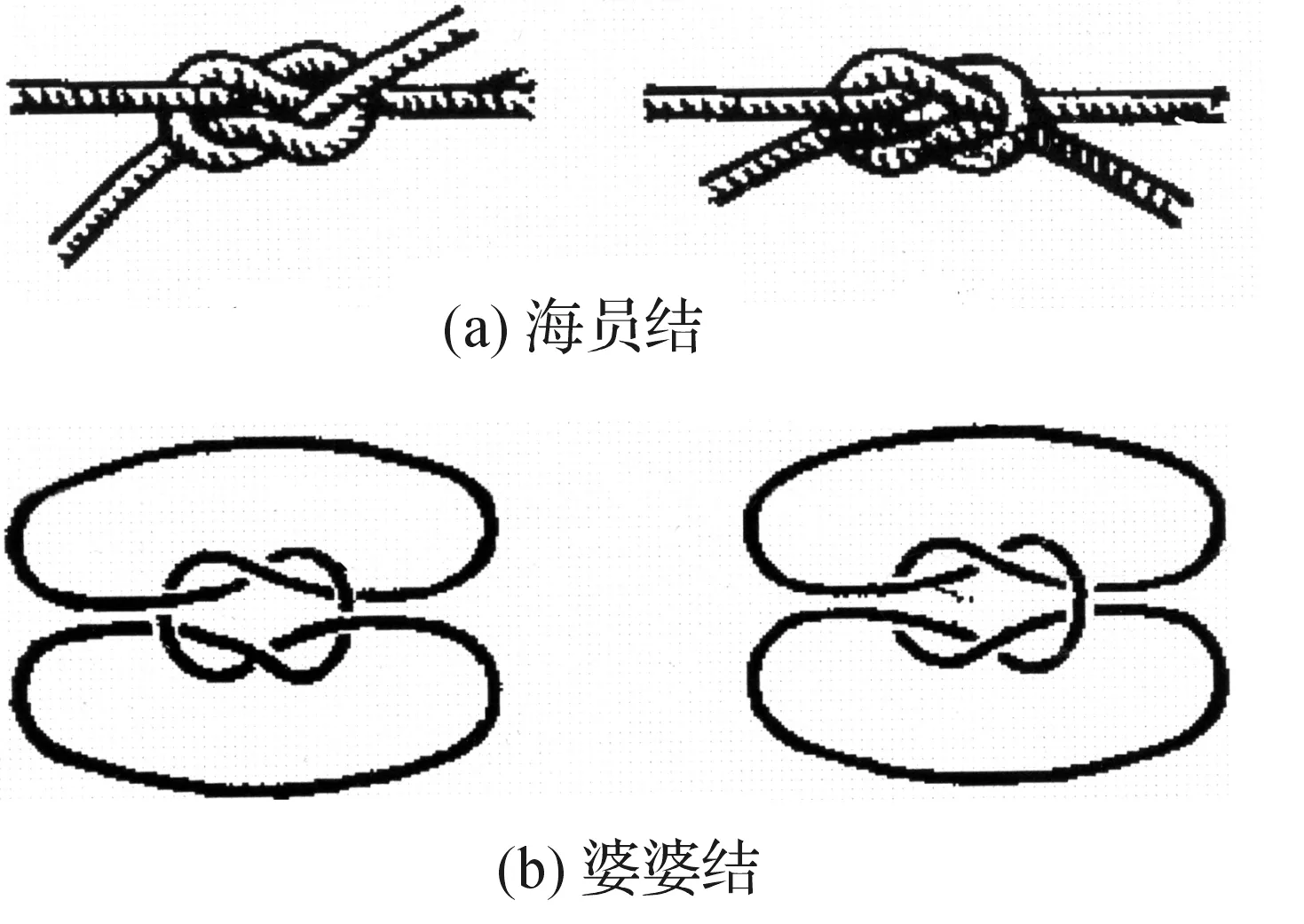
图4 2个不同痕的曲线Fig.4 Two different track curves

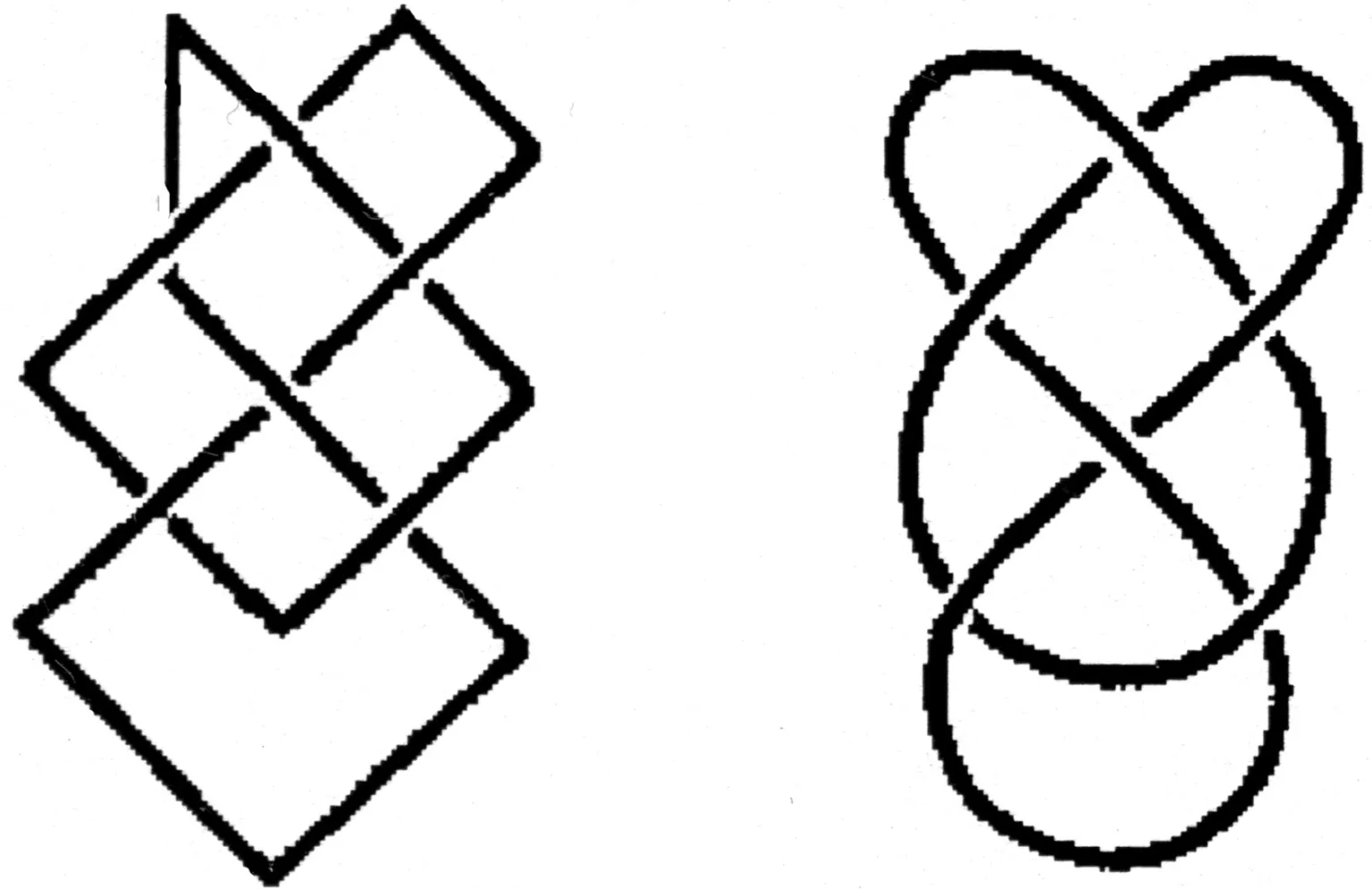
图5 2个同痕的曲线Fig.5 Two curves with common track

2 纽结(链环)类带形表皮的特征

纽结带形表皮除自绕之外一般并不是一条单独的表皮，而是多条带形表皮不仅在空间中的相互跨越，而且还可能自绕、互绕与环绕，是在一定的空间范围内由若干条表皮相互跨越、环绕组成的一个集合体。因此，这个集合体中每条带形表皮相互之间关系，包括表皮形状、彼此位置、层次安排等，都是互相影响的。除了纽结带形表皮的设计效果与每条表皮息息相关外，更加要强调这些纽结带形表皮构成的是统一的有机整体。纽结带形表皮由于在设计上具有其自身的特殊性，因此刻画纽结(链环)类带形表皮的复杂程度有几种指标，分别是交叉指标、桥指标、分支数和环绕方式。

2.1 交叉指标

一个纽结带形表皮的复杂程度最明显的指标是其投影图交叉点的个数。一个纽结(链环)类带形表皮的交叉指标，是指它的表皮投影图最少有多少个交叉点。一个链环类带形表皮的交叉指标n的意思是：它有一张n个交叉点的表皮投影图；它的每一张表皮投影图都至少有n个交叉点。交叉指标为0的纽结类带形表皮是平凡纽结带形表皮。纽结(链环)类带形表皮的表格通常都是依交叉指标排列的，如图6所示，自左向右：第1种结有4个交叉点，第2种有5个交叉点，第3种有6个交叉点，第4和第5种有7个交叉点[4]。

图6 纽结表皮的交叉指标Fig.6 Cross indexes of knot skin

2.2 桥指标

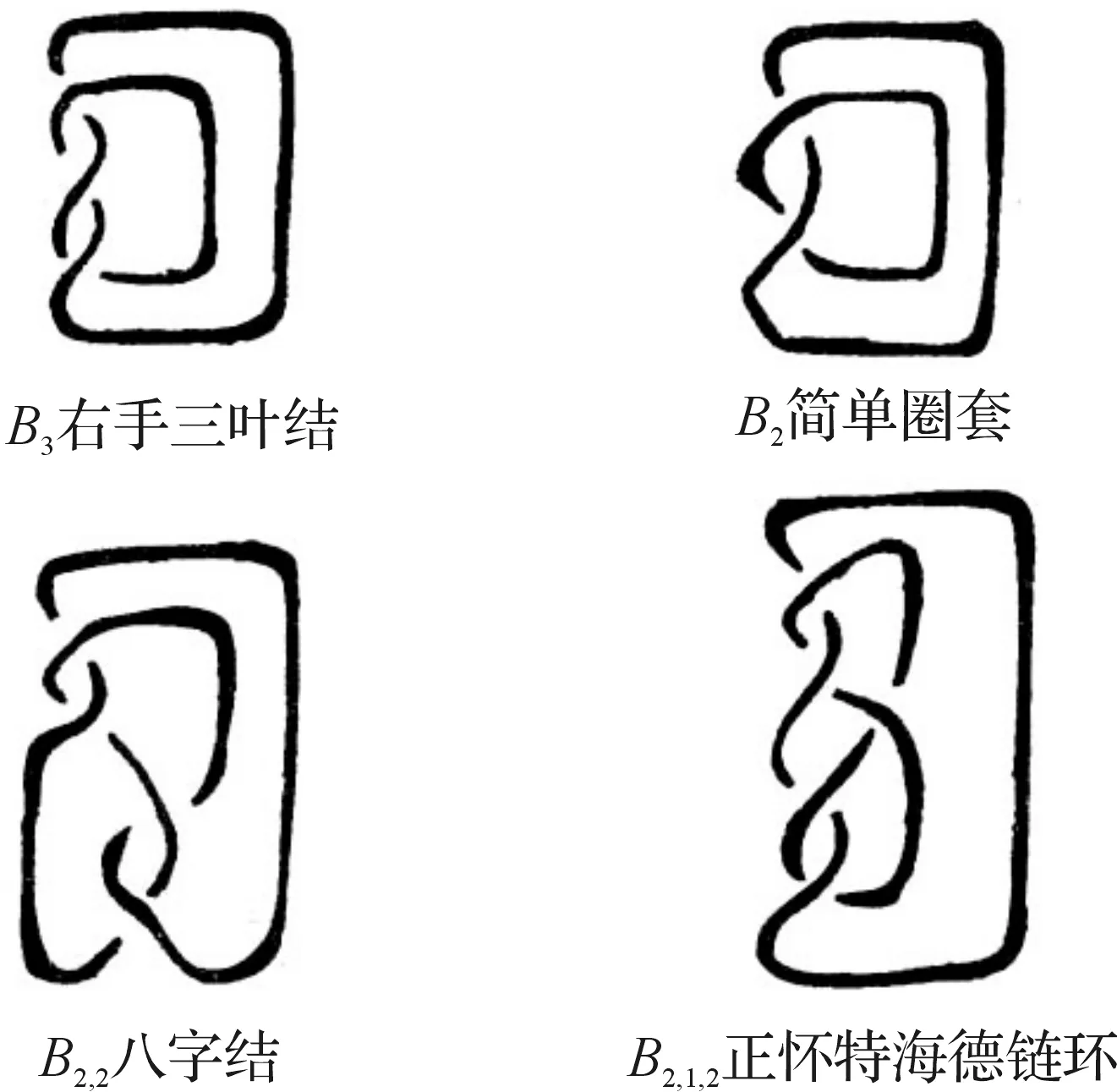
图7 纽结的桥拱数Fig.7 Numbers of bridge arch of knot

纽结类带形表皮是空间的一条简单带形闭曲面，其上的点有高有低，一般说来不会全部在一个水平面上 (全部在一个平面里的纽结类带形表皮一定是平凡的)。当沿纽结类带形表皮前进时，从逐渐上升到逐渐下降的一段称为一个桥拱，走过低谷后进入下一次起落算作另一个桥拱，这样每条简单带形闭曲面表皮被划分成若干个桥拱。对于给定的一个纽结类带形表皮，与该纽结类带形表皮结同痕的所有纽结类带形表皮中桥拱的最少个数，称为该纽结类带形表皮的桥指标，如图7所示。也可以说纽结类带形表皮桥拱数就是峰顶(比附近点都高的点)数或谷底(比附近点都低的点)数。桥指标为1的纽结类带形表皮一定是平凡纽结类带形表皮。所以桥指标可以作为衡量纽结类带形表皮复杂程度的指标[4]。

2.3 链环类带形表皮的分支数

2.4 纽结与链环类带形表皮的环绕

因为带形纽结闭合带形表皮在空间会发生环绕，纽结带形表皮的设计可以由较简单的纽结(链环)类带形表皮构造出更复杂的纽结(链环)类带形表皮，根据纽结带形表皮环绕的方式可分为自绕、互绕和混绕。

纽结带形表皮的自绕：如果是一个带形闭合带形表皮会发生纽结，即单环自身缠绕，称为自绕。如图8所示，福斯特设计的伦敦行政议会大楼中螺旋形的坡道是一个自绕的纽结带形表皮，呈现两头大中间小的哑铃形[6]。

图8 伦敦行政议会大楼坡道示意图Fig.8 Ramp schematic diagram of London parliament building

纽结带形表皮的互绕：如果是2个带形闭合带形表皮，即彼此不能游离，相互缠绕在一起，就好像链条上相邻的2个环一样的缠绕，称为互绕。如图9所示，德国设计师约格·施莱希设计的斯图加特基乐斯山观景塔上的2个纽结互绕的呈180°错开的螺旋式楼梯分别用于上下交通[6]。

图9 基乐斯山观景塔Fig.9 Killesberg Tower

纽结带形表皮的混绕：既有自绕又有互绕的多个(3个以上)带形闭合带形表皮的混合缠绕，简称为混绕。

纽结带形表皮设计所受制约因素较多，除受到结构和构造的制约外，纽结带形表皮结立体的表皮线型组合也十分复杂，表皮之间的分流、合流频繁，纽结带形表皮中弯、坡、斜表皮很多，而且经常带分岔，含变宽段，因此弯、坡、斜及加宽的地方空间布置处理就很复杂。纽结带形表皮立体空间造型较一般表皮要求要高，这是因为纽结带形表皮是全方位视阈的，其视阈的转换也是连续的，并且各个方向的视阈是相互竞争的。它强调的是各个方向视阈，不仅包括走在表皮的人，而且还包括行在表皮之外的人，而不是特指某个方向视阈。在不同方向的视阈，纽结带形表皮呈现不相同的形态，这种视阈的转换始终与纽结带形表皮在三维空间的延伸、发展联系在一起。

3 纽结类带形表皮的串联

在分析复杂的纽结类带形表皮时，为了简化，希望将其分解成几个简单纽结类带形表皮的串联连通和的形式，然后对简单的纽结类带形表皮再作详细分析。所以引出了纽结类带形表皮的连通和的定义：当一个纽结类带形表皮可以移动到某个位置，使得空间中某个平面与它只有2个交点，把该平面两侧的部分各用贴近平面的直线段封闭起来，分别得到2个纽结类带形表皮，即称原来的纽结类带形表皮分解为这2个新纽结类带形表皮之和。每个非平凡纽结类带形表皮可以分解成素纽结类带形表皮的连通和，而且这样的分解式是唯一的。素纽结类带形表皮是指那种非平凡纽结类带形表皮，它不能再分解成两个非平凡纽结类带形表皮的连通和了。例如三叶结、八字结、环面结、双桥结都是素纽结类带形表皮。在纽结类带形表皮理论中，通常很自然地把主要精力集中在研究素纽结类带形表皮和素链环类带形表皮，因为它们就是纽结带形表皮的基本构造单元，复杂的纽结类带形表皮与链环类带形表皮都是由它们搭建起来的。历史上所有的纽结类带形表皮[4]，如图10所示，都只列出素纽结类带形表皮。

图10 素纽结表皮排列图Fig.10 Arrangement of native knot track

先给定2个纽结类带形表皮K1，K2，怎样构造它们的和呢？在一条表皮上先后打2个素纽结，使它们串联在一起就构成2个素纽结的连通和。如图11所示。记作尺K1#K2。纽结带形表皮的连通和满足结合律，平凡结起着零的作用。在素纽结带形表皮的基础上，经过同痕拓扑变换(如环绕交叉和移位换形)就形成了基本造型单元。然后，以作为造型基本单元的素纽结带形表皮进行串联组成纽结带形表皮整体形态。需要注意的是素纽结带形表皮的基本造型单元不宜过多，不然会引起视觉上的混乱。对素纽结带形表皮进行拓扑变换时，除了满足自身功能之外，素纽结带形表皮串联组成纽结带形表皮整体形态必须要有形式的秩序感，不然会导致视阈的混乱。其形式组织因素要具有整体动态顺向的共同特性，这样将会产生一种韵律性动势、张力。在建筑中纽结带形表皮动势是不动之动，是“守静而治动”，纽结带形表皮是不可能看到真正的运动的，人们观赏到的是充满动感的线条，这些线条遵循整体形态的运动向某些方向上的倾向或集聚，作为一种贯穿整个建筑形体进而变成随视点游移的轮廓线，给人以动势的印象。

图11 纽结类表皮的串联Fig.11 Knot-shaped track in series

香港阿曼尼旗舰店由设计师Massimiliano Fuksas设计，设计师认为红色在中国代表着吉祥，人们在街道上经常看到飞舞的红绸带，如图12所示。于是，一条红色玻璃纤维带就被引入并贯穿了建筑空间，描绘出经过店里各部分的循环路线，顾客将随这条红带依次找到专卖店、咖啡馆、书店、花店和化妆品柜台[7-8]。在咖啡店里，红色玻璃纤维带弯曲扭转进入了入座区后表现出它狂野的一面，它在水平方向转弯和抬升，然后缠绕自己，一路上从吧台的台面延伸到桌子上，形成一个螺旋式上升的吧台和桌子，如图13所示。纽结结构不仅标示出通向咖啡馆的通道，而且界定了主要的销售区。在专卖店里，它从波形墙面那里找到平衡，又渐渐恢复常态，同天花板弯曲的照明带互相映衬。这2种弯曲的结构结合到一起产生双重效果，这条红带将静态的空间分隔成几个部分，如图14所示，整个空间因为这条纽结的红带而变得动感、前卫和时尚[7]。

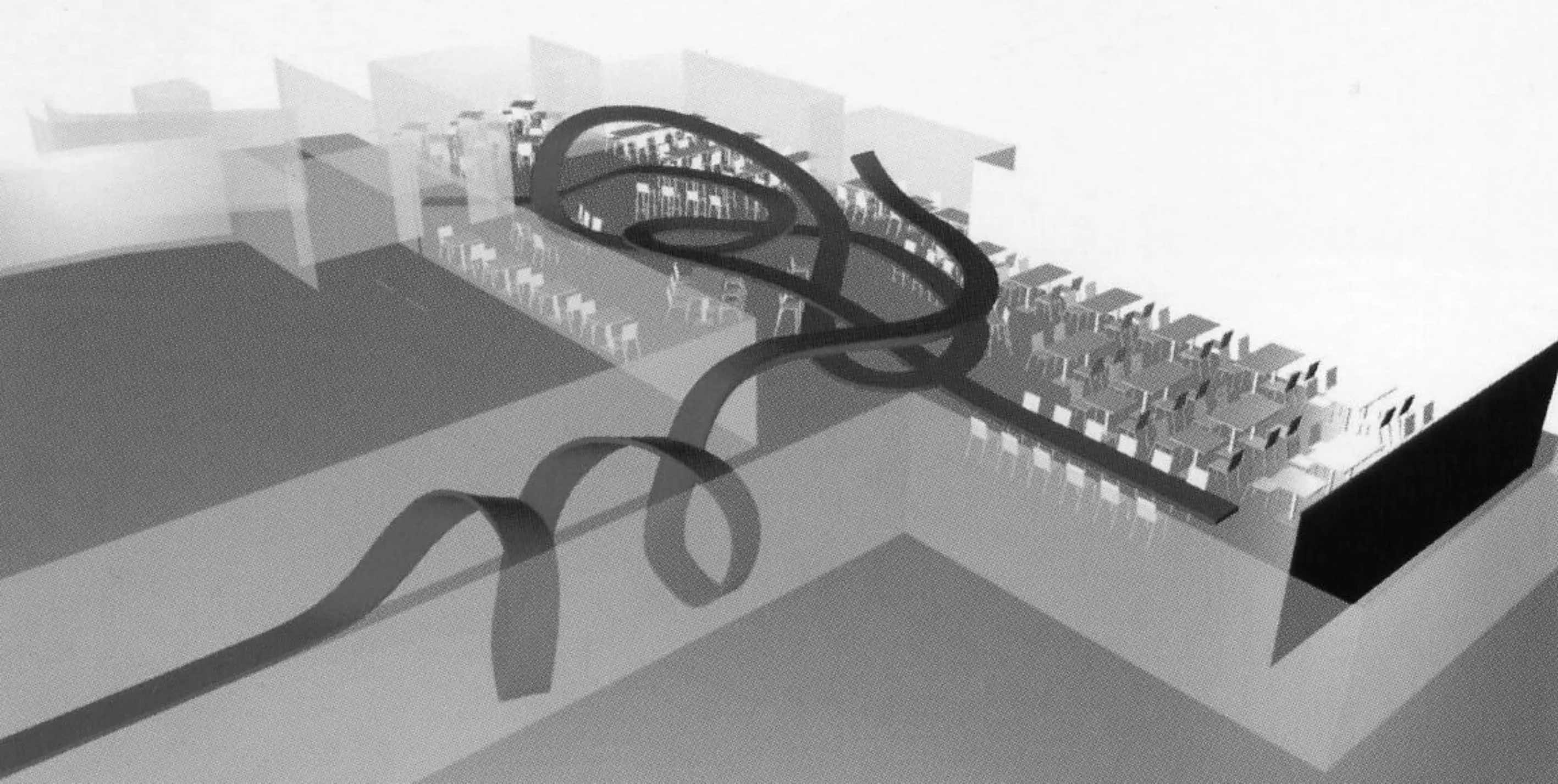
图12 阿曼尼旗舰店模型图Fig.12 Model diagram of flagship store of Amani

图13 入口处的纽结条带Fig.13 Knot-shaped entrance

图14 纽结的吧台桌面Fig.14 Knots-shaped buffet table’s top

4 链环类带形表皮的拼合

2个链环类带形表皮互相远离地拼合在一起，就构成一个新的链环类带形表皮，其分支数是原先那2个链环类带形表皮的分支数之和。这个新的链环类带形表皮就叫做先前2个链环类带形表皮的拼合；如果—个链环类带形表皮能分解为2个链环类带形表皮的拼合，这个链环类带形表皮就是可分离的，否则它就是不可分离的，如图15所示，它是那2个链环类带形表皮的拼合的投影图。

图15 链环类表皮的拼合Fig.15 Splice of link-shaped surface

链环类带形表皮的拼合特别强调整体纽结带形表皮的统一，使纽结带形表皮各个局部和谐一致地结合成整体，表现出浑然一体的形象。在链环类带形表皮的拼合设计中，各个表皮分支(各段素纽结带形表皮)的独立性和它的作用要准确地表现出来；同时，各表皮分支(各段素纽结带形表皮)的设计要体现整体观念，要考虑到对各部分空间的连通及对空间的围合作用。当表皮跨越时，链环类带形表皮上下表皮之间就其结构形式也有主表皮上跨与主表皮下穿立体交叉2种。对于链环类带形表皮拼合的统一主要采用2种手法：一是恰当处理表皮分支(各段素纽结带形表皮)对整体纽结带形表皮的从属关系；二是使构成一条纽结带形表皮的所有表皮分支(各段素纽结带形表皮)中的细部形状都相互协调。当主从关系求得统一时，局部表皮应从属于表皮整体的几何形状。链环类带形表皮总体造型统率整个表皮各表皮分支的布设，纽结带形表皮布设应顺应每条表皮分支的走向，根据带形表皮布设采用弯、坡、斜、曲线表皮及异形表皮。在同一条纽结类带形表皮的各段素纽结带形表皮中，形式应多样，因地选型，不单调重复。在注重个体形式特征的同时，还必须分清主次形式特征和整体形式统一，各段素纽结带形表皮串在一起构成空间中的珠链，必须与其所在空间融合成为一个整体，每一段素纽结带形表皮的个体形式特征也必须统一空间到这个大的整体形式特征中。

2001年OFIS建筑师事务所在欧洲住宅竞赛的获奖提案“波形之地”，选择奥地利格拉茨近郊的一块仓储和军事废地改造为一处住宅区，提出了一种带来新的社会和空间活力的城市再生组织模式。这种模式给予带有住宅、车库和花园的典型奥地利独户宅基地类型，运用了螺旋结构，将2块、4块或6块宅基地串成链环纽结带形，如图16所示，同时插入不同配比的公共设施，比如小商店、共享的办公空间、儿童游戏场地和庭院等，每一个链环的分支都被一个起伏的绿化屋顶所覆盖，如图17～18所示,容纳了由地坪标高变化的居住空间，创造了一个栖居之地[8]。

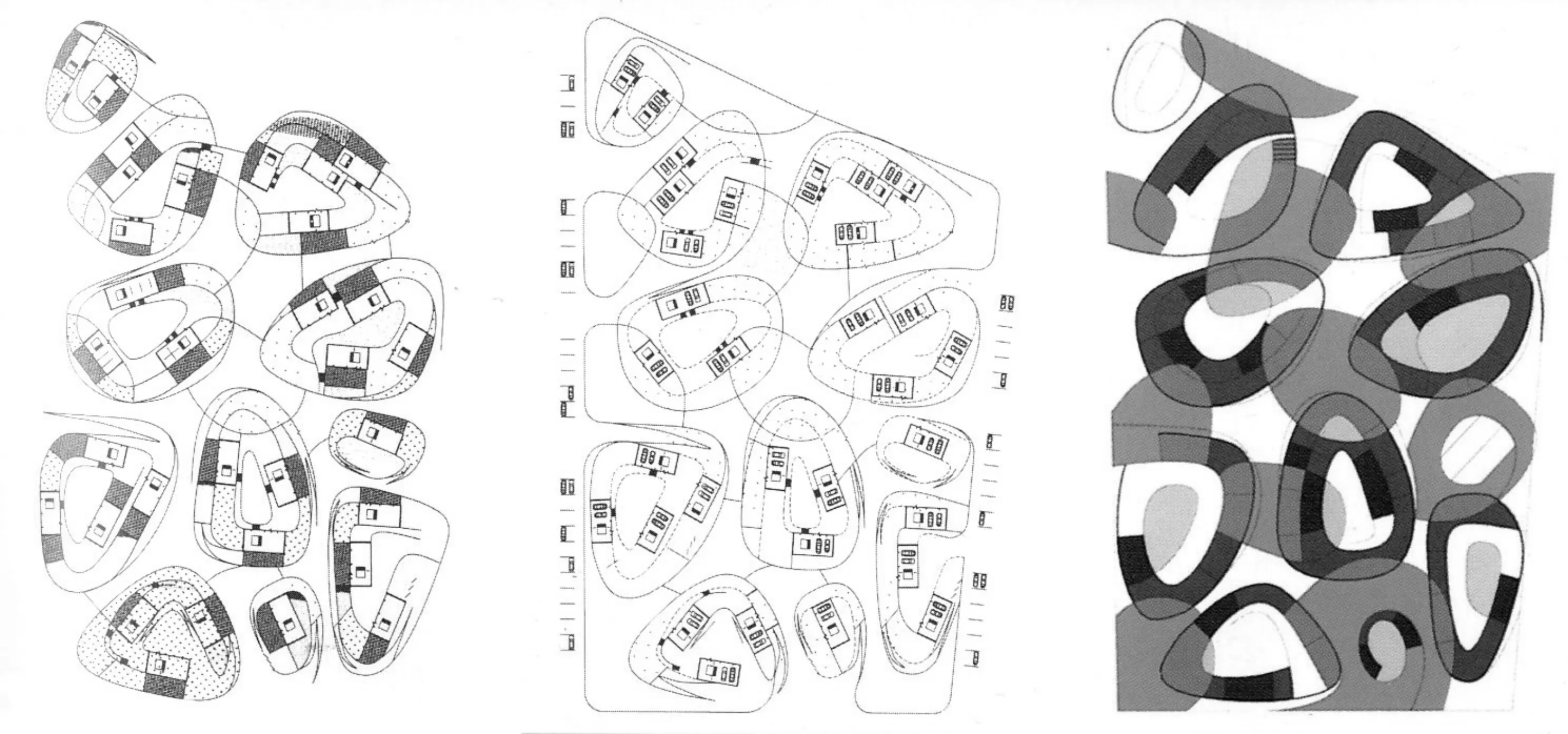
图16 “波形之地”构思图Fig.16 Conceive outline of “curly field”

图17 “波形之地”链环的一个分支Fig.17 A branch of link “curly field”

图18 “波形之地”纽结的链环Fig.18 Link of “curly field” knots

5 纽结(链环)类带形表皮与空间的形态融合

在考虑使纽结带形表皮与空间相结合时，一般有如下2种方法：一是融合法，使纽结带形表皮和空间相融合，纽结带形表皮的造型不能仅仅限于被动地服务于遮蔽功能，而且要使它的形式尽可能参与建筑空间的构成；二是强调法，着重运用空间视觉场原则分析纽结带形表皮的空间布置，强调突出纽结带形表皮在空间中的存在，纽结带形表皮应与周围空间环境组成富有层次序列的、有机统一的整体。

5.1 纽结类带形表皮占领空间

在建筑空间中，纽结类带形表皮具有“占领物”的意义，这种限定空间方式经常在以纽结类带形表皮为主的建筑空间中出现，在这种界定空间方式中，纽结类带形表皮成为了视觉焦点。由于纽结类带形表皮占领界定空间给人以扩散、被吸引的心理感受，纽结类带形表皮还利用自身和相互间的“张力”范围来界定出一个虽然无形但却明确有感的“空间范域”，人们从纽结类带形表皮界定的隐形范域中感受到空间关系的存在。空间范域辐射力与“占领物”纽结类带形表皮所构成的线性体量、环绕闭合性和透空度有直接关系。一般说来，纽结类带形表皮外轮廓线越高越宽，环绕闭合性越强，透空度越小，则空间的范域感越强，越明显；反之，则空间的范域感越弱，越模糊。

建筑师CAMPO BAELA在设计位于德国斯图加特的梅塞德斯奔驰博物馆时，整个设计贯穿一种清晰的概念——运动的概念，如图19～20所示。设计围绕着汽车与人的运动展开，以一个自我纽结的带形表皮为核心设计理念，这段自绕纽结带形表皮因特异而在整体中凸现，成为建筑造型的主节奏，组织起周围的空间。垂直向上的体量形成的张力强调了主体，从而形成了环境的主调。宽阔纽结的表皮既可以作为使汽车沿着螺旋表皮进入展览区，又可以作为参观者的参观路线，绝不重复地、一次性可以游遍所有展区。下部分有2个巨大柱敦支撑着盘绕着体量，盘旋着体量外部罩以透明表皮，使一切参观者与运动者清晰可见。随着新车型驶入展览馆，再伴随着如织的人群的运动形成一种别样的风景[9]。

图19 梅塞德斯奔驰博物馆构思图Fig.19 Concept design outline of Mercedes Benz Museum

图20 梅塞德斯奔驰博物馆Fig.20 Mercedes Benz Museum

5.2 链环类带形表皮围合空间

在建筑空间中，链环类带形表皮围合空间是以各种有形的表皮分支通过交织环绕而形成空间，使人们感受到空间范域的存在。建筑空间和链环类带形表皮空间互相渗透，隔而不断。链环类带形表皮围合界定空间是在空间中以分支表皮划出一个“单元”，在其中建立起相对独立的活动秩序。而链环类带形表皮围合空间效果也是与其闭合性、透空度相关；闭合性越强、透空度越小，空间的范域感越强；反之，空间的范域感越弱。

建筑师S. J. Hong在设计阿鲁普公司伦敦总部新大楼的空间结构时，主要采用在其链环状线形办公区域内部设计一些“结点”的方法，如图21所示[4]。这种相互连接的链环状空间结构，使得单一的部门可以与其他各部门相互融合，这样各部门工作小组及项目小组就形成了嵌套的层级关系。这种链环状空间结构既避免了各部门的完全分隔，又保证了一定的空间独立性，是一种使圆形环状交通空间既具有领域感又适用的策略。这种链环状的设计方案满足了客户的需求，以立体的链环形结构有效地保证了各部门区域既自成一体又相互联通的设计特点[10]。

图21 阿鲁普公司伦敦新总部Fig.21 New headquarters for Arup in London

6 结 语

随着纽结带形表皮在非线性建筑中的应用日趋广泛，逐渐彰显出拓扑学的纽结理论在纽结带形表皮中的重要作用及其与一般表皮理论的区别。纽结带形表皮设计是表皮设计中的重要组成部分，纽结带形表皮不仅是建筑的皮肤，而且也是建筑中的视觉焦点，因此设计必须重视其美学效果。纽结带形表皮的功能美、形式美与周围地形地貌共同构成新景观的复杂不规则结构，给表皮设计分析带来了新的难题。由于拓扑学中纽结理论的一些法则对纽结带形表皮设计具有一定的借鉴性，因此，可以帮助设计人员解决一些设计纽结带形表皮时遇到的难题。

[1] 亚尼齐.拓扑学(英文版)[M]．北京：世界图书出版公司，2012：56-78.

[2] 李滨泉，李桂文.建筑形态的拓扑同胚变化[J]．建筑学报，2006(5)：51-54.

[3] 李滨泉，莫天伟.建筑表皮的拓扑剖分[J]．华中建筑，2008(10)：71-76，84.

[4] Crowell R H, Fox R H. Introduction to Knot Theory[M].New York: Springer-Verlag，1977：62-64.

[5] Rolfsen D. Knots and Links[M]．Rhode Island：Amer Mathematical Society，2003：32-36.

[6] Muir H.The Phaidon Atlas of Contemporary World ArchitectureⅡ[M].London：Phaidon Press Ltd,1999：27-29,37-38.

[7] Agora+Patterns. internatial Architecture DesignⅠ[M].London：Phaidon Press Ltd,2004：48-57.

[8] Hasting J. 100 Architect 10 Critics[M]. London：Phaidon Press Ltd,2005：52-58.

[9] Lindberg S. International Architecture Exhibition TrajectoriesⅠ[M]. New York ：Rizzoli International Publications Inc，2004：55-65.

[10] Muir H. The Phaidon Atlas of Contemporary World ArchitectureⅢ[M]. London：Phaidon Press Ltd，2004：38-50.

Topologyanalysisonknot-shapedskinofarchitecture

LI Binquan

(School of Architecture and Civil Engineering, Zhejiang University of Science andTechnology, Hangzhou 310023, China)

With the development of architectural technology, the complex knot-shaped skin is adopted in more and more architecture designs. Most architecture designs are limited to the perceptual level because of lack of the systemic theory as direction. Therefore it is necessary to do rational and systemic thinking under the direction of theory. This paper introduces the knots in topology to direct and analyze the design of knot-shaped skin. Firstly, the paper starts with analyzing the topological characteristics of knot-shaped skin to put forward the regularity of mold-making about knot-shaped skin and link-shaped skin. Secondly, it uses Jones’ multinomial to explain invariant with identical track of knot-shaped skin in topology. Then, it sets forth complexity of knot-shaped skin and surrounding, connecting and splicing among knot-shaped skins. We try to use topology of knot theory to solve some problems encountered in the design of construction of knot-shaped skin.

topology; knot theory; topological identical track; knot-shaped skin; link-shaped skin; surrounding

TU201.1; TU12

A

1671-8798(2013)06-0447-11

10.3969/j.issn.1671-8798.2013.06.009

2013-09-27

浙江科技学院学科交叉预研专项资助项目(2011JC06Y)

李滨泉(1970— )，男，辽宁省辽阳人，副教授，博士，主要从事建筑形态学研究。