天然气处理厂放空火炬系统的稳定性分析

署恒木，魏升龙，杨 远，宋作苓，潘秀珍

(1.中国石油大学储运与建筑工程学院，山东青岛 266580;2.北京石油化工工程有限公司西安分公司管道室，陕西西安 710075)

在高架火炬管的分析中，一般考虑火炬的回火、热辐射、排放量及壁厚强度等方面的设计［1-2］，未考虑稳定性因素。而且关于管道强度分析的文献［3-10］也只考虑管道内压所引起的管道环向变形和环向应力，并未考虑内压对管道稳定性的直接影响。在工程中确实发生过塔架系统结构破坏的情况，引起火炬塔架系统倒塌的原因是管道内部的流体压力引起管道的失稳破坏造成的。流体内压对管道稳定性的直接影响不能忽略［11］，因此在考虑内压情况下，对高架放空火炬的稳定性分析非常必要。笔者以苏里格气田第四处理厂的放空火炬系统为研究对象，分别利用能量法和有限元分法对其进行稳定性分析，得到稳定破坏的临界条件。

1 火炬管临界屈曲时的能量平衡方程

图1为火炬管与塔架示意图及火炬管与塔架之间的约束图。

图1 火炬管与塔架示意图及火炬管与塔架之间的约束Fig.1 Schematic diagram of flare and tower，constraint between flare and tower

图2为火炬管的力学模型、屈曲图及微弯的气柱。火炬管上端自由、下端固定;将火炬与塔架之间的实际约束方式简化为弹簧约束，弹簧约束比简支端约束更接近实际约束情况。得到弹簧的弹性系数十分困难，提出了一种简便有效的方法，即通过有限元分析得到结构的约束弹簧系数。设火炬管上端受到的实际作用力的合力为轴力N;管内外均有气体存在，重度分别为γi、γo;管上端内外气体压力分别为pi与po;内外圆的截面面积分别为Ai与Ao，q为单位长度火炬管的重力。当轴力N不断增大达到临界状态时，火炬管处于微弯状态。考虑火炬管与内部气体整个系统的能量平衡，此时内部气体与管之间的压力变成内力，不考虑其做功。

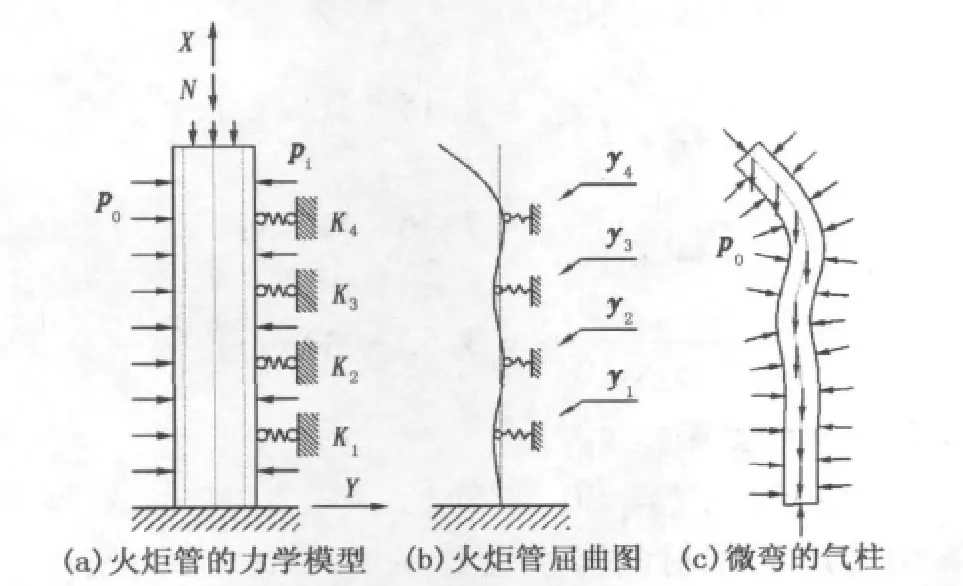
图2 火炬管的力学模型、屈曲图及微弯的气柱Fig.2 Mechanical model and buckling map of flare，slightly crooked air column

当火炬管处于屈曲临界状态时，外力功的增量应等于变形能的增量［12］，即

火炬管微弯时变形能增量为

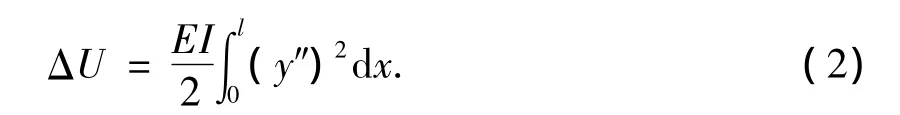
由于弯曲使得x截面处沿X方向的位移增量为

管自重做功增量为

等价于［12］

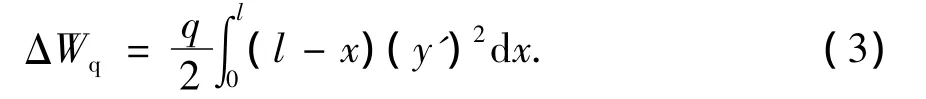
管上端轴向压力N做功增量为

管上端内部气压做功增量为

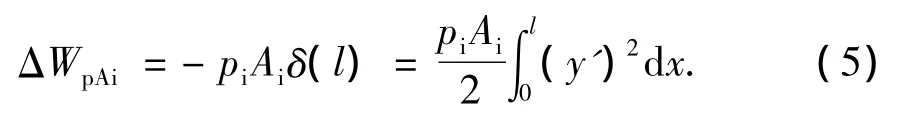
管内部气体自重做功增量为

其中，qi=Aiγi。

直接计算管外部侧向气压做功增量ΔWpo很困难。根据虚功原理［13］，取与微弯后的火炬管完全相同的气柱(图2(c))，在微弯过程中，气柱所受气压做的功与气柱自重做功之和为零，则

式中，ΔWPAo为气柱上端气压做的功;ΔWqo为气柱势能的增量。

则

图2(b)中，假设4个弹簧约束的变形量自下而上分别为 y1，y2，y3，y4，设对应的弹簧系数分别为K1，K2，K3，K4，则弹簧约束做功增量为

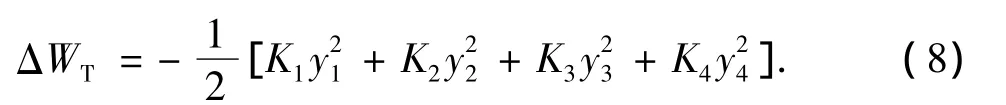
将式(2)～(8)代入式(1)中得到

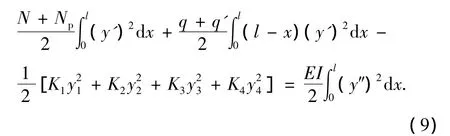
其中

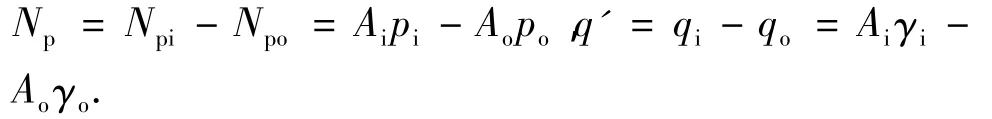
式(9)即为放空火炬管临界屈曲时的能量平衡方程。

2 火炬管挠曲线函数

各约束弹簧的变形量即火炬管的弯曲横向位移自下而上分别为 y1、y2、y3、y4。火炬管的挠曲线函数应分别满足弹簧约束条件和下端条件。

设函数 w满足位移约束条件 w(0)=0，

为了满足下端y'(0)=0的条件，设函数y=w+g，其中g是多项式函数，在各个约束处的位移等于零。则

式中，k为未知数。

根据条件y'(0)=0，则得

则火炬管的挠曲线函数y为

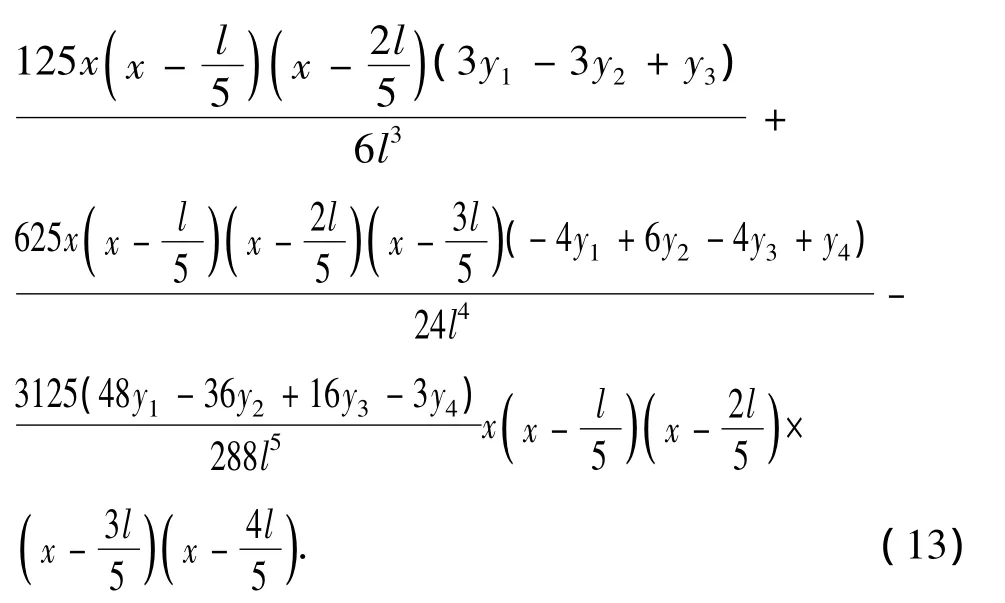
式(13)即为满足所有约束条件及边界条件的位移函数。

“八八战略”彰显强大的实践力量。如今，在“八八战略”实施15周年之际，2018年7月8日，习近平总书记对浙江工作专门作出重要指示。他强调，干在实处永无止境，走在前列要谋新篇，勇立潮头方显担当。

3 参数计算

3.1 弹簧约束的弹性系数

利用ANSYS软件建立塔架的有限元模型，不建立火炬模型。分析塔架结构可知，Y方向跨度要比X方向跨度大，说明塔架更易沿X方向弯曲变形，因此当放空火炬管处于临界屈曲状态时，火炬管也更易沿X方向发生屈曲变形。

在火炬管与塔架的某一约束点处沿X方向施加单位力F=1，并计算获得该约束点在力方向上的位移值S。根据弹簧弹力 =弹性系数×变形量，则可计算得到该约束点所对应的弹簧约束的弹性系数。同理可得其他位置弹簧约束的弹性系数(所对应的约束位置自下向上，见图2(a)):

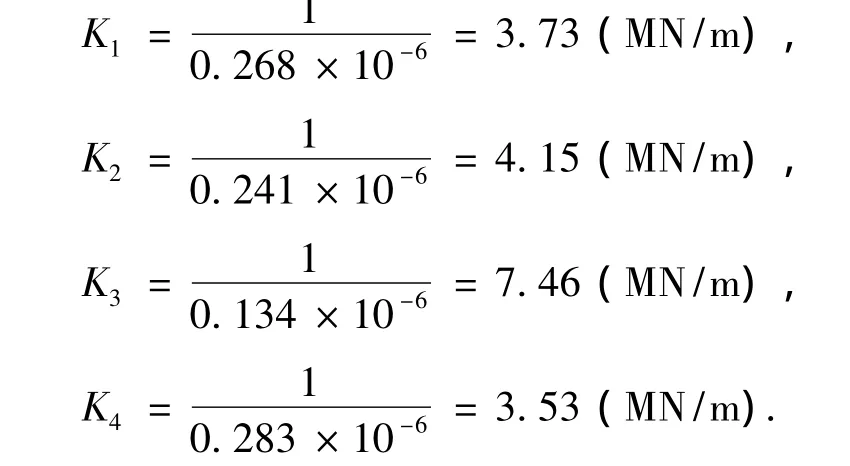
3.2 其他参数

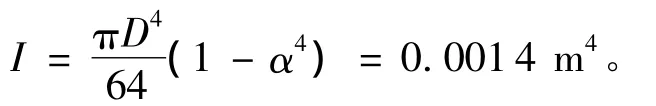
放空火炬内部气压取其设计压力，为0.6 MPa，火炬管外部气压取标准大气压，为0.1 MPa;在天然气处理厂放空过程中甲烷气体占放空气体成分的95%以上，故气体相对分子质量Mg=16 kg/kmol;气体压缩系数 Z=0.98，气体常数 R=8.314 kJ/(kmol·K)，管内气体温度为50℃，管外气体温度为20℃。则

将 K1，K2，K3，K4，E，I，l，q，q' 及式(13)代入式(9)，整理得

4 结果计算及稳定性判断

此时问题转化为有约束非线性规划问题，求解函数最小值，利用MATLAB软件进行数值求解。

临界屈曲状态时火炬管微弯，火炬管与塔架的约束点处的位移一般不超过0.05 m，故 y1、y2、y3、y4的范围取为［－0.05，0.05］，即:

用MATLAB软件求解的结果见图3。

图3 N+Np值随迭代次数的变化Fig.3 Curve of N+Npas a function of iteration number

由图3可判断目标函数N+Np收敛。且此时:y1=0.0212 m，y2=0.0125 m，y3= －0.0335 m，y4=0.0498 m 且 min(N+Np)(y1，y2，y3，y4)=a/b=2.6738 MN，则放空火炬管的临界屈曲载荷Flj=2.6738 MN。

由火炬管内外气压及放空气体反作用力所引起的对火炬管口的垂直反力的计算公式为［14］

式中，W为气体质量流量，kg/s;v为气体流速，m/s;pi为火炬管出口处管内侧气压(绝压)，Pa;po为标准大气压，Pa;DLF为动载因子(按放空瞬间最大冲击时考虑，取DLF=2)。

对比垂直反力FN=0.46 MN与临界屈曲载荷Flj，即可判断火炬管的稳定性安全。

当放空火炬结构参数一定时，其临界屈曲载荷也是唯一确定的。由式(14)可知，当放空火炬处于临界屈曲状态时，N+Aipi－Aopo=min(a/b)=P，其中，P为确定数。由该式可知，当内压pi增大时，火炬管可承受的轴向压力N将减小，即内压降低火炬管的稳定性;当外压po增大时，火炬管可承受的轴向压力N将增大，即外压增强火炬管的稳定性。

5 有限元分析

建立塔架及放空火炬的有限元模型。

在第一次屈曲分析中，在放空火炬顶端施加竖直向下的单位荷载，分析计算得到模型的一阶屈曲力为2.0858 MN，此时不考虑重力作用。

在第二次屈曲分析中，在放空火炬顶端施加竖直向下的力F，大小为2.0558 MN;此时考虑重力作用，重力加速度为9.8 m/s2。分析得到屈曲载荷因子为1。说明所施加的载荷即为一阶屈曲力。

放空火炬的屈曲模态见图4。

图4 一阶屈曲模态及局部放大图Fig.4 The first buckling mode and partially amplified result

从图4可知，放空火炬的一阶屈曲模态为扭曲螺旋状，与曾发生过的火炬管的实际破坏状态基本一致。对火炬管及塔架的三维有限元屈曲分析得到的一阶屈曲力为2.0558 MN，对比能量法求得的一阶屈曲力的数值解为2.6738 MN，考虑到模型简化及数值求解带来的误差以及能量法自身的方法误差，则可以认为两种方法所求得的结果是十分相近的。

6 结论

(1)分别利用能量法和有限元法求得了放空火炬管临界屈曲载荷，两种方法所得的结果十分相近。

(2)内压降低火炬管的稳定性，外压增强火炬管的稳定性。火炬管内部气压对稳定性的影响等效于在火炬顶端作用一个轴向压力和沿管轴线作用一个均匀分布方向向下的载荷;火炬管外部气压对其稳定性的影响等效于在火炬顶端作用一个轴向拉力和沿管轴线作用一个均匀分布方向向上的载荷。

［1］ 叶学礼.天然气集输站场放空立管设计［J］.天然气工业，1995，15(3):61-67.YE Xue-li.The design of flare in natural gas collection and transportation station［J］.Natural Gas Industry，1995，15(3):61-67.

［2］ 张晓刚，范冬立，刘新岭，等.特大型高含硫天然气净化厂安全放空与火炬系统设计解析［J］.天然气工业，2012，32(1):90-93.ZHANG Xiao-gang，FAN Dong-li，LIU Xin-ling，et al.Safe and efficient vent and flare technology for the purification plant dealing with over ten billions m3high H2S natural gas annually in the Puguang Gas Field，Sichuan Basin［J］.Natural Gas Industry，2012，32(1):90-93.

［3］ LUBINSKI A.Influence of tension and compression on straight and buckling of tubular goods in oil wells［C］.Uthur Lubinski:Developments in Petroleum Engineering，Stability of Tubular，1987.

［4］ 阿英宾杰尔A B等.干线管道强度及稳定性计算［M］.肖冶，等，译.北京:石油工业出版社，1988:74-101.

［5］ 杨明华.海洋油气管道工程［M］.天津:天津大学出版社，1992:48-52.

［6］ ERGUN Kuru，ALEXANDER Martinez，STEFAN Miska，et al.The buckling behavior of pipes and its influence on the axial force transfer in directional wells［J］.Journal of Energy Resources Technology，2000，122:129-135.

［7］ SOREN R，HAUCH，YONG Bai.Bending moment capacity of pipes［J］.Journal of Offshore Mechanics and Arctic Engineering，2000，122:243-252.

［8］ 帅健，王晓霖，叶远锡，等.地面占压荷载作用下的管道应力分析［J］.中国石油大学学报:自然科学版，2009，33(2):99-103.SHUAI Jian，WANG Xiao-lin，YE Yuan-xi，et al.Stress analysis of pipeline subject to surface load［J］.Journal of China University of Petroleum(Edition of Natural Science)，2009，33(2):99-103.

［9］ 赵冬岩，余建星，岳志勇，等.含缺陷海底管道屈曲稳定性的数值模拟［J］.天津大学学报，2009，42(12):1067-1071.ZHAO Dong-yan，YU Jian-xin，YUE Zhi-yong，et al.Numerical simulations on buckling stability of subsea pipelines with imperfections［J］.Journal of Tianjin University，2009，42(12):1067-1071.

［10］ LUIGINO Vitali，LORENZO Marchionni，ROBERTO Bruschi，et al.The role of internal pressure in the deformation capacity of pipelines［J］.The Journal of Pipeline Engineering，2011:41-56.

［11］ 署恒木.流体压力对油气管道轴向稳定性的影响［J］.油气储运，2000，19(8):27-30.SHU Heng-mu.The influence of internal and external liquid pressure on critical buckling load of pipeline［J］.OGST，2000，19(8):27-30.

［12］ 铁木辛柯.弹性稳定理论［M］.张福范，译.北京:科学出版社，1958.

［13］ 罗维东.有限变形弹性体的广义虚功原理［J］.石油大学学报:自然科学版，1999，23(5):60-62.LUO Wei-dong.A generalized virtual work principle of finite elastic body［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，1999，23(5):60-62.

［14］ 唐永进.压力管道应力分析［M］.北京:中国石化出版社，2003:100-101.