基于权重矩阵的模糊决策模型及城市金融聚集度评价

李 丽

(武汉理工大学经济学院，武汉 430070)

1 引言

多目标多维模糊决策是从评价对象组成的系统出发，根据建立的目标函数得到决策模型，依据决策的优化标准，通过对多个决策方案的优选，同时得到评价对象的最优评价指标权重、等级标准、模糊划分和加权综合值，最后根据模糊划分判定评价对象的类别，依据综合值的大小进行优劣排序［1］。对多目标决策而言，合理确定目标权重是判定决策方案优劣的关键问题之一［2］。众多学者对主观定权法［3］、客观定权法［4］、组合定权法［5］等进行了深入探讨，取得了大量的研究成果［6－7］。在多目标决策时，权重确定往往不可避免的受到主观因素的影响，即具有不确定性［8］;并且现有的多目标决策方法提供的仅是一维决策信息即加权综合值［9］。为此，文［10］从系统分析出发，根据目标权重信息的不确定性和目标加权综合值划分的模糊性，基于多目标综合值的模糊划分，提出了多目标多维自反馈模糊决策模型，为无模式多维模糊决策问题和确定权重提供了一种新途径。但对多目标多维决策问题，由于不同目标在不同类别中的作用程度可能不同，传统的目标权重向量表达形式就具有一定局限性。因此，本文将权重向量拓展为权重矩阵，提出了基于权重矩阵的多目标多维自反馈模糊决策模型，并应用于中国中部五城市金融聚集度评价决策，得到了较为满意的结果。

2 多维自反馈模糊决策模型

在多目标多维决策问题中，不同目标在不同类别中的作用程度可能不同。例如在职称评定中，设主要评价指标有“教学水平”、“科研水平”和“管理水平”，而这三个评价指标在“高级”、“中级”和“初级”职称晋升考核中的作用程度显然是不同的。因此，在这种情况下将权重向量拓展为权重矩阵是必要的。基于权重矩阵的多维自反馈模糊决策模型的主要计算步骤如下。

2.1 计算多目标的综合值

设多目标决策方案集为A=(A1，A2，…，An)，j=1，2，…，n;目标集为B=(b1，b2，…，bm)，i=1，2，…，m;n个决策方案的m个目标值用决策目标特征值矩阵表示为A=(aij)m×n。为克服不同目标量纲、量级上的差异，将决策目标特征值矩阵转化为规范化决策矩阵R=(rij)m×n。

设将n个决策方案分为c 类，且m个目标在不同类别中的作用程度不同，决策方案的目标权重矩阵为W=(wih)m×c，且wih≥0，，则第j个方案的多目标决策加权综合值zj为

显然，若已知目标权重矩阵，则由(1)式可计算n个决策方案的多目标综合值，用向量表示为

2.2 计算多目标综合值的模糊划分

设决策集的n个决策依据指标(2)式划分为c个类别，设模糊识别矩阵为

式中，uhj表示决策j 隶属于h 类的相对隶属度，h=1，2，…，c.(3)式应满足条件

依据单指标模糊识别理论，计算最优模糊识别矩阵U*和最优模糊聚类中心指标G*的循环迭代公式为

式中，xj表示决策j 综合值zj的规格化值［10］，0≤xj≤1;gh表示第h个类别的中心指标，0≤gh≤1;h=1，2，…，c。

显然，只要给定决策集的分类数，就可以依据多目标的加权综合值，计算得到最优模糊划分U*，依据最大隶属原则可判别个决策所属类别。

2.3 计算多目标聚类中心

在已知决策集最优模糊识别矩阵U*的情况下，依据成因分析和多目标模糊识别理论，可计算出各目标对应的聚类中心.设m个目标在c个分类的情况下，模糊聚类中心矩阵为

式中，sih表示第h 类别指标i 的规格化值，且0≤sih≤1.计算sih的公式为

显然，由(3)，(8)式可求得最优多目标模糊聚类中心矩阵S*。

2.4 计算多目标权重矩阵

为了求解最优目标权重矩阵W*，建立模糊环境下带有监督因子和稳定系数的目标函数，即

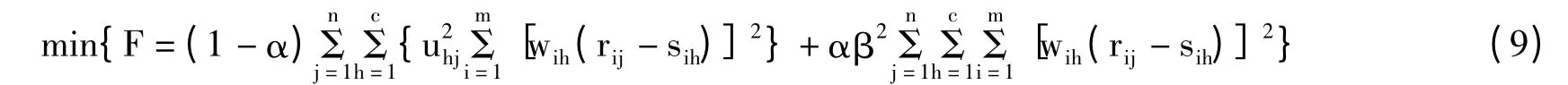
式(9)的数学物理含义为:全体决策到所有类别的加权广义权欧式距离平方(uij为权)与全体决策到所有类别的广义权欧式距离平方(wih为权)的加权和最小(α为权)。

在已知unj和sih的情况下，根据权重矩阵等式约束和目标函数(9)式，建立无约束的拉格朗日函数，求导并整理得计算wih的公式

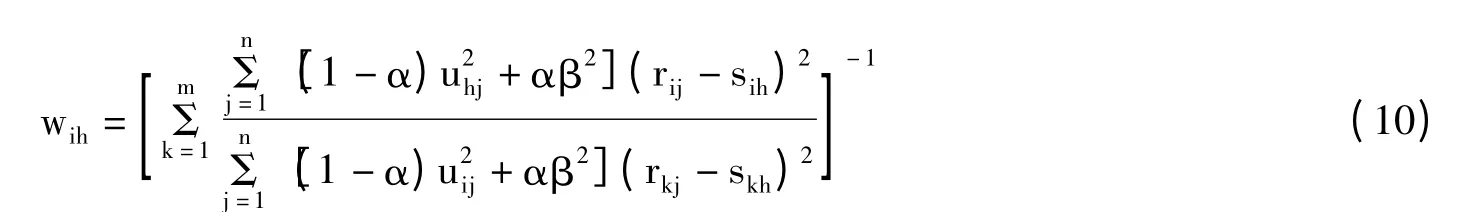
式中，α为权重矩阵监督因子，β为稳定系数，且0≤α≤1.

显然，由(7)，(10)式可求得最优目标权重矩阵W*，通过调整α和β 值即可得到符合主观意愿的最优目标权重矩阵。

2.5 多维自反馈模糊决策算法

在给定m个目标的初始权重、监督因子α和稳定系数β 的情况下，首先给定权重矩阵初值，由(1)式计算出n个决策方案的多目标综合值，根据多目标综合值由(5)，(6)式计算出n个决策方案的模糊识别矩阵U*，由(8)，(10)式又可以计算出m个目标的聚类中和权重矩阵，再由(1)式计算出n个决策方案的多目标综合值。这种算法构成了自迭代计算过程，具体算法步骤如下。

(1)将决策目标特征值矩阵A=(aij)m×n转化为相对优的规范化决策矩阵R=(rij)m×n。

(2)给定目标加权综合值计算的精度ε，给定决策模式数c和各目标初始权重矩阵。

(3)给定稳定系数β。

(4)给定目标权重监督因子α。

(6)根据综合值Z0，由(5)，(6)式循环迭代计算各决策的模糊识别矩阵。

(9)逐个比较Z1与Z0对应的分量，若，则计算结束.否则，若，则重复计算步骤(6)～(9)，直至满足计算的精度要求为止。

由此可见，求解最优决策目标加权综合值Z*代结果的条件为

式中d 表示为循环迭代次数。

(10)若计算的目标权重不符合决策者的主观意愿，则调整主观监督因子α，重复第(5)～(9)步进行迭代计算，直至计算结果满足主观要求为止。

(11)若以上计算的目标权重仍不符合决策者的偏好，则调整稳定系数β，重复第(4)～(9)步进行迭代计算，直至计算结果满足主观要求为止。

显然，根据上述计算方法可以得到近似最优各决策的目标加权综合值向量Z*，同时得到各决策的近似最优模糊划分识别矩阵U*。由目标加权综合值向量Z*，依据越大越优的原则，可以进行决策的优劣排序和确定最优决策。由模糊划分识别矩阵U*，根据最大隶属原则，可以判定各决策所属的类别。

3 应用实例

金融集聚可以为所在地带来巨额资金，促进金融机构之间的协作和资源共享，提高信息传递的效率;并通过规模经济、辐射效应，对区域经济发展产生深刻的影响.随着中部崛起步伐的加快，为谋求区域金融主导权，拥有和支配更多金融资源，中部各大城市纷纷将金融发展和建设区域金融中心纳入各自的长远发展规划。整个中部的区域金融布局尚未敲定，对于处于竞争中的任一城市而言，都有必要明确自身金融资源集聚的相对优势及弱势，以便准确定位、科学发展［11］。本文以武汉、长沙、郑州、南昌、合肥中部五城市为研究对象，利用基于权重矩阵的多目标多维模糊决策模型对中部五城市金融集聚程度进行综合评价。

参照国内外相关文献，建立金融集聚程度的指标体系，并将评价指标划分为目标层、准则层和因子层(表1)。以中部五城市2001－2010年的数据为样本进行金融集聚的度量和比较，研究所需的数据主要来源于相应年份的《中国统计年鉴》、《金融统计年鉴》、《中国城市统计年鉴》，以及各城市的统计局网站和中国经济社会发展统计数据库等，对于缺失的数据，采用灰色预测方法进行补充。

取决策模式数c=3 时，采用本文给出的模型及算法，令ε=0.0001，给定不同α和β 值计算目标权重矩阵，得到一组决策解。经综合分析，本文最后取c=3，α=0.44，β=0.333 作为模型的最佳参数，利用本文算法经过4 次迭代计算，分别得到了综合值的聚类中心向量G、各决策类别的多目标聚类中心矩阵S、权重矩阵W、最优模糊决策识别矩阵(略)和历年加权综合值(见表2)，按金融聚集度历年平均值越大越优的原则，对中国中部五城市金融聚集度进行优劣排序，结果列于表3。根据表2，中国中部五城市历年金融聚集度发展趋势见图1。

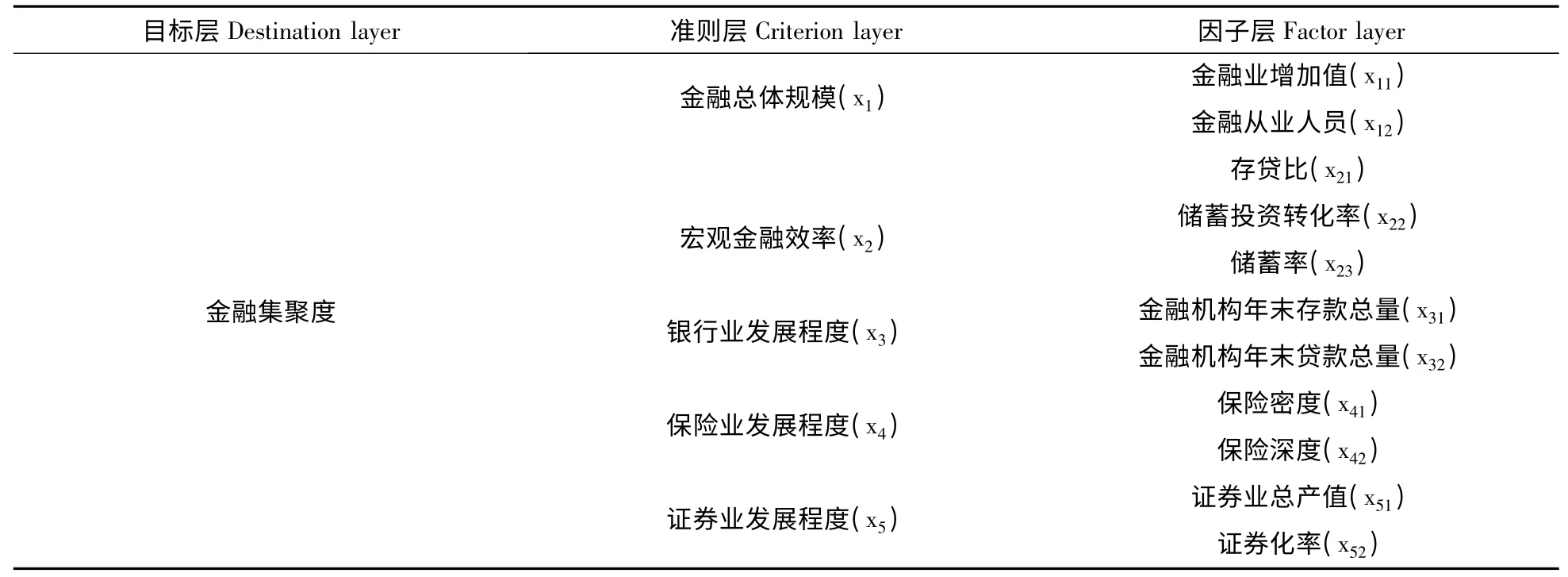
表1 金融集聚评价指标体系Table 1 The evaluation index of city finance contagion

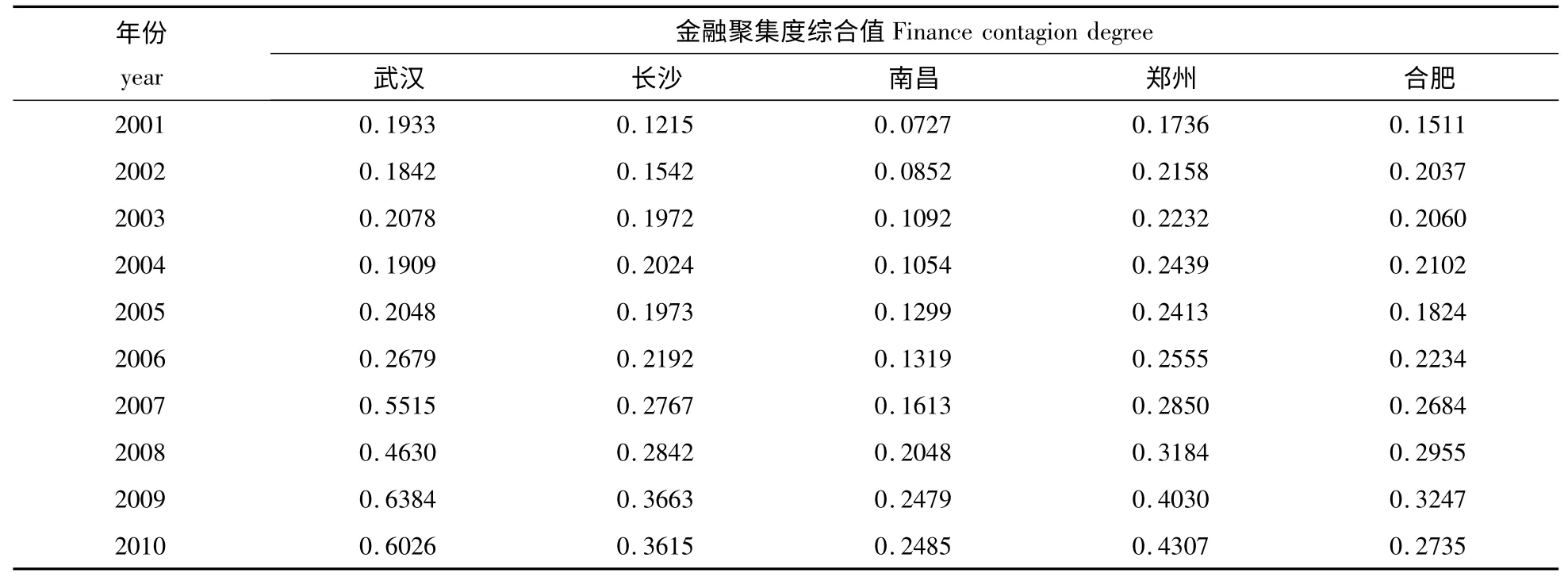
表2 中部五城市历年金融聚集度Table 2 The finance contagion degree of Chinese five center cities

表3 中部五城市历年平均金融聚集度及排名Table 3 The finance contagion degree and ranking of Chinese five center cities

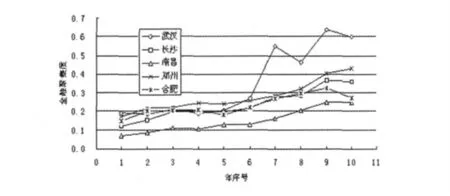
图1 中部五城市历年金融聚集度趋势Fig.1 The finance contagion degree trends of Chinese five center cities

根据图1 结合原始数据可以发现，除了2010年受金融机构年末贷款等因素的影响，五个城市的金融集聚均有不同程度的影响以外，2001－2009年五个城市金融集聚程度呈现出整体增强的趋势。武汉的金融集聚程度一直保持强势，长沙、郑州的金融集聚发展较为平稳，南昌历年的金融集聚程度相对偏低，而郑州的金融集聚程度由弱逐年变强，且近年来发展比较平稳。由表3 可见，2001－2010年武汉、长沙、南昌、郑州、合肥的平均金融聚集度分别为0.3504、0.2380、0.1497、0.2791、0.2339，因此，中部五城市金融聚集度的综合排名为武汉、郑州、长沙、合肥、南昌。这一结果与实际相符。

为对比说明，再采用因子分析法计算中部五城市的金融聚集程度。对比分析两种方法的评价结果表明，多维模糊决策模型的评价结果更为合理。多维模糊决策方法的评价结果不仅能较好地反映中部五城市的金融聚集程度和发展趋势，而且各城市间的金融聚集度具有较大的离散性，更容易进行优劣排序。

4 结束语

本文将权重向量扩展为权重矩阵，提出了基于权重矩阵的多目标多维自反馈模糊决策模型，丰富了多维模糊决策理论。该模型数学基础严密，物理含义明确，易于程序化。中国中部五城市金融聚集度综合评价决策实例说明模型是有效的、权重矩阵更能全面地反映各目标在不同决策类别中的作用。

［1］李希灿，王 静.具有稳定系数的多目标多维模糊决策算法［J］.模糊系统与数学，2007，12(6):128－134

［2］徐泽水.多属性决策的两种方差最大化方法［J］.管理工程学报，2001，15(2):11－13

［3］Mon D L，Cheng C H，Lin J C.Evaluation Weapon System by Analytical Hierarchy Process Based on Entropy weight［J］.Fuzzy Sets and Systems，1994，(62):127－134

［4］丁世飞，王启田.基于信息熵的PCP 综合决策模型研究［J］.小型微型计算机系统，2007，28(1):79－82

［5］王才宏，杨世容，董 茜.目标选择决策的组合熵权系数方法研究［J］.弹箭与制导学报，2006，26(4):377－380

［6］徐泽水.部分权重信息下对方案有偏好的多属性决策法［J］.控制与决策，2004，19(1):85－88

［7］王 煜，徐泽水.OWA 算子赋权新方法［J］.数学的实践与认识，2008，38(3):51－61

［8］邓聚龙.灰色预测与决策［M］.武汉:华中科技大学出版社，2005

［9］LI Xican，WANG Jing，WANG Fang.The Pattern of Multiple Attribute and Multiple Dimension Grey Decision Making［J］.The Journal of Grey System，2007，20(3):273－280

［10］李希灿，王 静.多目标多维自反馈模糊决策模型［J］.控制与决策，2010，25(2):241－245

［11］胡国晖，李 丽.中部五城市金融集聚程度及影响因素比较研究［J］.西部金融，2013，14(1):73－78