PCA算法和数学形态学理论在踝臂指数测量中的应用

户鹏飞，迟鹤翔，刘宝华，2

（1．燕山大学河北省并联机器人与机电系统实验室，河北秦皇岛 066004;2．北京航空航天大学自动化科学与电气工程学院，北京 100191）

0 引言

踝臂指数（ankle-brachial index，ABI）是踝部动脉收缩压与双侧肱动脉收缩压的最高值之比，它是诊断外周动脉疾病（peripheral artery disease，PAD）的一种简便、无创的方法［1］。因此，测量ABI的关键在于准确测量出上肢和下肢的动脉收缩压。目前，测量动脉收缩压的主要方法是双层袖带测量法，使用该方法可以准确测量出上肢肱动脉收缩压。但是人体下肢有多条动脉，而且前胫骨动脉和腓骨动脉在胫骨和腓骨之间，导致无法利用袖带加压来完全阻断这2条动脉的血液流动。所以，即使在很高的压力下仍然可以监测到幅值很高的脉搏波波动［2］。此时检测到的信号会是多条血管的脉搏波叠加后的波形，在叠加后的脉搏波波形图中，用直观的方法很难分辨出重新恢复血液流动时的第一个脉搏波，所以，在下肢的收缩压测量中准确地识别脉搏波重新恢复波动的起点成为关键。

为了准确找到下肢脉搏波重新恢复波动的起点，本文利用主成分分析（PCA）算法，将采集的脉搏波信号进行分离，从而找到被加压袖带阻断的血管的脉搏波信息，并用基于数学形态学的梯度原理来处理分离后的脉搏波，从而成功找到脉搏波重新恢复波动的起点，为准确测量ABI提供依据。

1 PCA

1．1 动态嵌入

为了应用PCA分离采集到的脉搏波，需要多维脉搏波数据，但受袖带体积和人体小腿尺寸以及实际的需要，必须减少传感器数量。因此，实际检测过程中只能用一维信号进行分离，这样的分离系统属于欠定系统。参照参考文献［2］应用的动态嵌入 （dynamical embedding，DE）技术构建采样时间序列，尽可能不失真地还原脉搏波信号。

DE即通过对观察得到的连续时间矢量进行延迟，得到新的状态空间［2，3］。确定延迟矢量维数后，就可以由大量的连续延迟矢量构建内嵌式矩阵，其表达形式如下

式中N为信号长度，τ为延迟，m为内嵌式矩阵维数。

1．2 PCA

PCA是一种常用的基于变量协方差矩阵对信息进行处理、压缩、抽提的有效方法。该算法可以用于数据的降维，是一种统计分析技术，其目标是找到数据分布方差最大的方向，并将数据向该方向投影并保持投影后恢复数据的残差最小。对数据降维时，计算输入数据向量的相关矩阵Rxx的特征值和特征向量，然后将原始向量投影到m个优势特征值对应的特征向量空间。

用PCA算法进行信号分离时，假设经动态嵌入后得到的矩阵为X，其协方差矩阵为C。对X进行PCA的过程就是求其协方差矩阵C的特征值λ对应的标准正交特征向量V的过程，即满足公式

然后，按照特征值的大小对提取出来的主分量进行排列［4］，得到相应的解混信号。

通过袖带采集的踝部脉搏波数据包含多条动脉信息，人体踝部有4条主动脉。这些动脉血管深浅不一，脉动强度有所不同，故能量也有所差异，适合从能量的角度进行分离。PCA就是从信号的能量角度进行分析，把这些动脉信息分离的过程就是从采集的一维脉搏波信号中进行主分量提取的过程。分离后的脉搏波通过人眼识别可以轻松找到脉搏波恢复跳动的起点，但是对于计算机来说，识别第一个脉搏波的峰值仍然具有一定难度，这就需要将峰值的特征更加显著化，用数学形态学处理分离后的脉搏波可以达到这个要求。

2 数学形态滤波与波形提取

2．1 数学形态学原理

数学形态学是在集合论和积分几何的基础上发展起来的非线性分析方法。它是用一个已有的结构元素去度量被处理信号。结构元素相当于一个“探针”，根据结构元素的不同，可以有效地对信号中所含的信息进行提取。

数学形态学的基本算子主要包括腐蚀运算、膨胀运算，以及以此为基础构造的开、闭运算等。这些算子的定义如下:

设原始信号f（n）为定义在F=（0，1，2，…，N－1）上的离散函数，定义结构元素g（n）为G=（0，1，2，…，M－1）上的离散函数，且N≥M，则f（n）关于g（n）的腐蚀和膨胀分别定义为

f（n）关于g（n）的开运算和闭运算分别定义为

式中 Θ为腐蚀运算，⊕为膨胀运算，◦为开运算，·为闭运算［5］。其中，开运算可以抑制信号的正脉冲，即削去信号中比结构元素宽度小的波峰。闭运算可以抑制信号的负脉冲，即填平信号中比结构元素宽度小的波谷。开、闭运算本身和它们的自由组合可以形成不同的形态滤波器。为了同时滤除信号中的正脉冲和负脉冲，通常采用形态开、闭的级联形式。采用相同尺寸结构元素，通过不同顺序级联开、闭运算定义的形态组合滤波器如下

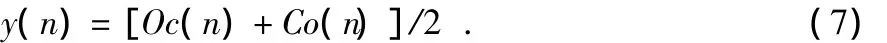
由于开运算的收缩性导致开—闭滤波器的输出偏小，而闭运算的扩张性导致闭—开滤波器的输出偏大，因而，存在统计偏倚现象。但是，开—闭和闭—开组合形态滤波器避免了上述缺点，可以使信号尽可能保持其原有幅值和波形［6］。

2．2 数学形态学梯度

f（n）关于g（n）的梯度运算定义为

基于扁平结构元素的膨胀和腐蚀运算具有取信号的局部极大和局部极小值的功能，形态学梯度即为二者做差，取局部范围内的最大与最小值之差，可用于信号的边缘检测［7，8］。

数学形态学的各种变换完全是在信号的时域内进行，无关于信号的频域信息，运算结果只取决于信号的局部形态特征，对局部内信号的变化有较强的识别能力，且运算速度快。对进行ABI测量的脉搏波信号而言，只需要识别其波形，不需要深究其幅值、频率等信息;在进行ABI测量时，也只需要观察信号局部的特性——信号各个周期幅值的对比。所以，数学形态学变换适合和PCA算法进行结合，用于ABI的测量。

3 实验结果与分析

图1是一组典型的测量ABI时的脉搏波数据。被测者为健康成年人，用双袖带方法测得的踝部脉搏波波形。

图1 脉搏波原信号Fig 1 Original signal of pulse wave

对图1的采样数据根据动态嵌入技术构建130维内嵌式矩阵，进而用文中提到的PCA分解算法进行解混。解混后的脉搏波波形图如图2所示，本文只列出了前6个分量，后面的基本为噪声信号，不予列出。分析分离后的脉搏波信号，前4个分量能较清晰地辨别出为脉搏波信号，符合人体下肢踝部有4条主动脉的事实，该PCA分离方法为有效分解。

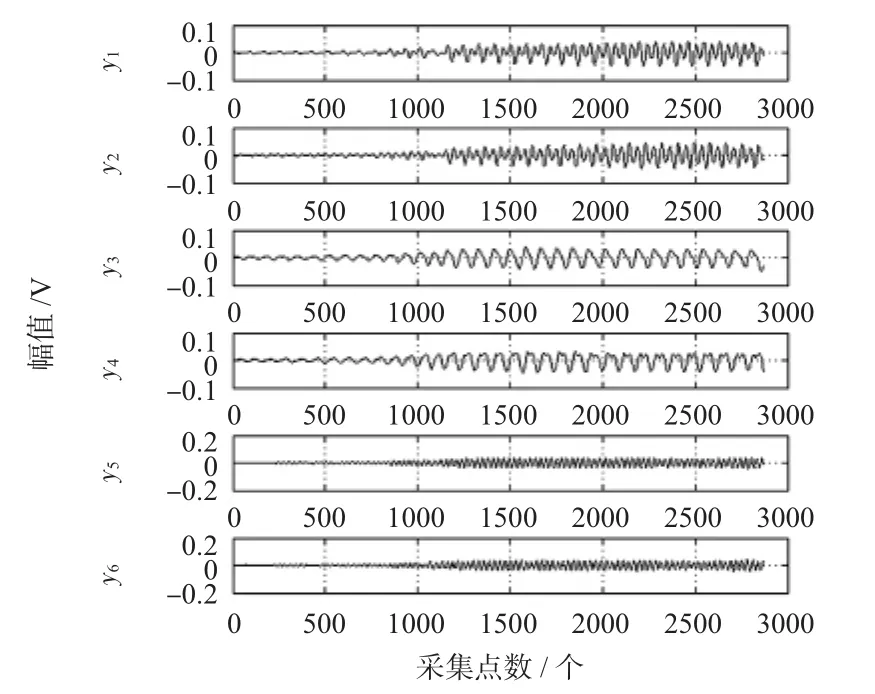
图2 解混后的脉搏波信号Fig 2 Pulse wave signal after separating

对分离后的脉搏波信号用公式（7）所示的原理进行滤波，滤波时，结构元素宽度的选取对滤波结果有很大影响［9］，这里选择宽度为8的直线型结构元素。对处理后的动脉脉搏波求其梯度，选取结构宽度为50的直线型结构元素。结果如图3所示。分析脉搏波信号的梯度图，在图上可以清楚地看出:在1000点过后的第2个周期（圆圈标出的位置），脉搏波梯度有一个斜率较大的陡升。该脉搏周期所对应的压力值即为下肢收缩压。同分离后的信号波形图进行比较，梯度图中波峰更明显地显现出来，应用计算机更容易识别到该点峰值，进而选取该时刻的袖带压力作为收缩压进行ABI的计算。一般来说，较浅层的动脉信号易被加压袖带阻断血流，当压力减小恢复脉搏跳动时，浅层的动脉脉动传播到传感袖带的能量也较大，排序也相对靠前。

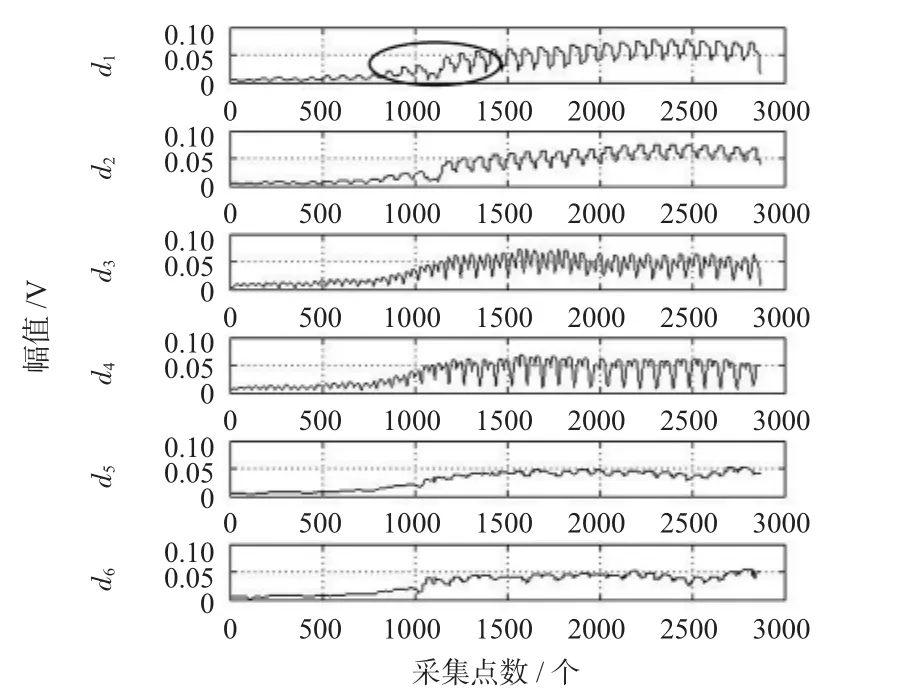
图3 脉搏波信号梯度图Fig 3 Gradient figure of pulse wave signal

4 结束语

本文先利用PCA算法对采集的下肢脉搏波信号进行分离，利用基于数学形态的梯度理论对分离后的下肢脉搏波数据进行处理，实验结果证明:这种方法可以很好地找到下肢动脉在袖带放气过程中重新恢复脉搏波动的起点。与传统的方法相比，这种方法简单快捷，识别准确，为ABI的准确测量提供了一个新的思路。

［1］ Kenneth O．Peripheral arterial disease［J］．The Lancet，2001，358:1257－1264．

［2］ 刘宝华，戴成武．EVD算法在踝臂指数测量中的应用［J］．传感技术学报，2010，23（1）:19 －23．

［3］ James C J，Lower D．Extracting multisource brain activity from a single electromagnetic channel［J］．Artificial Intelligence in Medicine，2003，28:89 －104．

［4］ 马建仓，牛奕龙，陈海洋．盲信号处理［M］．北京:国防工业出版社，2006:36－46．

［5］ 欧阳森．改进数学形态方法及其在电能质量监测中的应用［J］．华南理工大学学报:自然科学版，2005，33（2）:34 －38．

［6］ 李 刚，何宏献，刘 巍，等．数学形态滤波器及其在心电图机中的应用［J］．仪器仪表学报，1999，20（4）:335 －339．

［7］ Li B，Zhang P L，Wang Z J，et al．Gear fault detection using multiscale morphological filters［J］．Measurement，2011，44:2078 －2089．

［8］ 郑 涛，刘万顺，肖仕武，等．一种基于数学形态学提取电流波形特征的变压器保护新原理［J］．中国电机工程学报，2004，24（7）:18 －24．

［9］ 胡爱军，孙敬敬，向 玲．振动信号处理中数学形态滤波器频率响应特性研究［J］．机械工程学报，2012，48（1）:98 －102．