微电网多目标动态优化调度模型与方法

洪博文，郭 力，王成山，焦冰琦，刘文建

（天津大学 智能电网教育部重点实验室，天津 300072）

0 引言

随着微电网技术的不断推广应用，如何妥善管理微电网内部分布式电源和储能的运行，实现微电网经济、技术、环境效益的最大化成为重要的研究课题[1]。由于微电网内能源结构、分布式电源类型和控制方式的多样性，微电网的能量管理和优化运行具有较高的复杂性[2-3]。同时，考虑微电网本身的多目标属性，传统的以大型发电机为主的单目标调度优化方法难以适应复杂的微电网环境[4]。

目前，微电网的调度策略分为固定策略和优化策略[5-7]2种，其中优化策略又可分为静态优化和动态优化。固定策略以事先拟定的设备优先级制定运行规则，该优先级不随系统的运行环境发生改变；静态优化根据当前时刻或时段系统的运行环境下各设备的运行成本，确定其优先级和运行方式；动态优化考虑一个调度周期（包含多个时段）内的运行成本，以调度周期内的总收益最高或总成本最低为目标，优化系统运行。由于动态优化考虑了多时段设备运行之间的协调配合，对于通常含有储能、发电机等时间耦合特性元件的微电网，优化效果更理想[8]。

在优化调度模型的求解方面，遗传算法和多目标进化算法因良好的并行性、鲁棒性和全局优化能力为学者所青睐[9-12]，但其效果受到初始点选取的影响。文献[13]针对含发电机爬坡率约束的动态经济调度问题，使用模拟退火法为遗传算法寻找初始迭代点，提高遗传算法的收敛速度。文献[14]则结合动态经济调度的具体问题，提出了遗传算法种群初始化的多种方法，除按各设备的容量、发电成本关系确定调度方案以获取对应的初始种群外，还引入了线性规划的方法。但上述种群初始化方法主要针对单目标的遗传算法，并未涉及多目标进化算法。文献[15]运用梯度的方法对多目标进化算法NSGA-Ⅱ进行了种群初始化操作，并对算法改进的效果进行了检验。但文献[15]未对算法的具体应用进行研究，且其改进方法由于需要对优化问题进行求导，不适用于复杂的动态优化调度问题。

本文以经济和环境成本最小为目标，建立了微电网多目标动态优化调度的一般模型，采用改进的NSGA-Ⅱ进行求解。改进算法在初始化阶段采用初始值引导技术，即首先通过单目标的遗传算法获取NSGA-Ⅱ初始种群的部分个体，以提高算法的收敛性能。以典型微电网为例，分析了本文所建模型和所提方法的有效性。

1 系统仿真模块

1.1 系统模块设计

本文采用模块式设计结构[16]构造优化调度模型的主框架，如图1所示。

图1 优化调度模型基本组成模块关系图Fig.1 Relation between basic modules of optimization model

图1中包含输入模块、输出模块、系统仿真模块和运行优化模块4个部分，模块之间通过数据交互实现优化目标。

输入模块主要提供模型所需的数据和参数，其中包括系统组成、元件参数、发电和负荷数据、优化算法参数等；输出模块主要输出优化调度方案和目标值等优化结果。

系统仿真模块和运行优化模块是调度优化模型的核心组成部分，通过两者之间的数据交互共同实现调度优化目标。其中，系统仿真模块主要通过能量模型仿真系统在准稳态条件下的运行特性，对系统运行方案的技术、经济、环境等指标进行评估；运行优化模块综合不同方案的指标评估结果，采用启发式的方法得到优化的方案。优化过程中，运行优化模块将种群个体对应的运行方案传递给系统仿真模块，由仿真模块对方案进行指标评估，然后将评估结果以个体适应度的形式传递给优化模块。

1.2 仿真模型

1.2.1 光伏发电系统模型

光伏阵列的功率输出如下[17]：

其中，fPV为光伏系统的功率降额因数，表示光伏系统实际输出功率与额定条件下输出功率的比值，一般取0.9；YPV为光伏阵列容量（kW）；IT为地表水平面实测光照度（kW／m2）；IS为标准测试条件下的光照度，一般取 1 kW／m2；αP为功率温度系数（%／℃）；Tcell为当前光伏电池的表面温度（℃）；Tcell，STC为标准测试条件下的光伏电池温度，一般取25℃。

1.2.2 风机模型

风机功率计算公式如下：

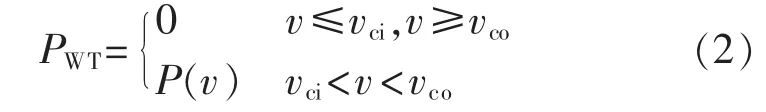
其中，v为风机轮毂高度处的实际风速；vci、vco为切入风速和切出风速，当实际风速低于切入风速或高于切出风速时，风机都不工作；P（v）为正常风速范围内风机出力，由风速-功率特性曲线线性插值得到。

1.2.3 蓄电池模型

假定蓄电池为铅酸蓄电池，其模型采用Kinetic Battery Model（简称 KiBaM）模型[18]，同时假定电池端口电压恒定、各时步内电池的充放电电流恒定，不考虑环境条件的影响。

电池组在任意时刻储存的总能量等于可用能量与束缚能量之和，即：

其中，W1为可用能量；W2为束缚能量。

依据电池组实际充放电功率，可计算出充放电后电池组的可用能量：

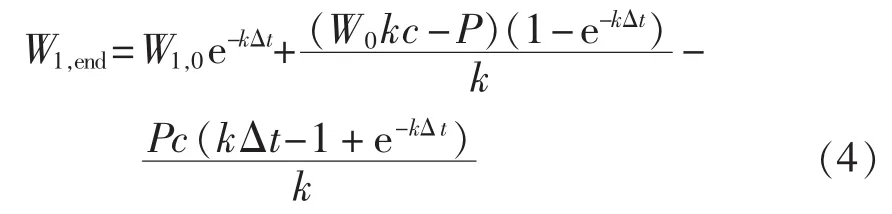
其中，W1，0为初始时刻电池组的可用能量（kW·h）；W1，end为终止时刻电池组的可用能量（kW·h）；W0为初始时刻电池组的总能量（kW·h）；P为电池组放电（为正）或充电（为负）功率（kW），不包含充放电损耗；Δt为时间间隔（在算法中亦即时间步长，h）；c为电池容量比例，表示蓄电池满充状态下可用能量和总能量的比值；k为电池速率常数（h-1），表示可用能量与束缚能量的转化速率。

结合式（3）和式（4），同时考虑到总能量减少量等于放电电量 P Δt，可得到充放电后电池组的束缚能量：

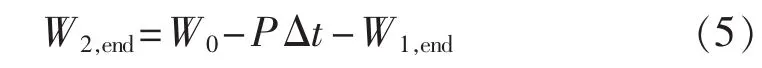
其中，W2，end为终止时刻电池组的束缚能量（kW·h）。

任意时刻可用能量W1满足关系式：0≤W1≤cWmax，其中 Wmax表示蓄电池最大可存储能量（kW·h）。结合时间步长终止时刻可用能量W1，end计算式（4），可以得到蓄电池KiBaM模型单步最大允许充电功率和最大允许放电功率，分别为：

为防止蓄电池的过充、过放，最大充电功率约束中还应计及蓄电池的最大充电电流和速率约束，得到对应的最大充电功率（kW）分别为：

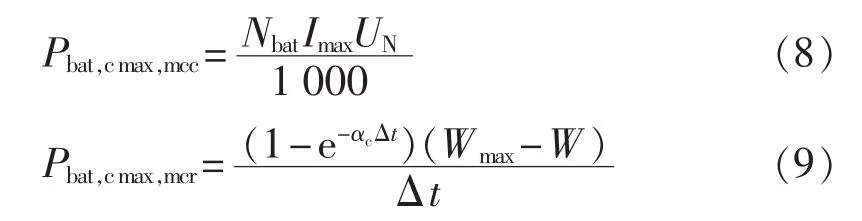
其中，Nbat为电池串并联总数；Imax为电池的最大充电电流（A）；UN为电池的额定电压（V）；αc为电池的最大充电速率（A／（A·h））。

结合KiBaM模型中对蓄电池充放电功率的限制，并计及充放电损耗，得到最终的蓄电池充放电功率限制为：

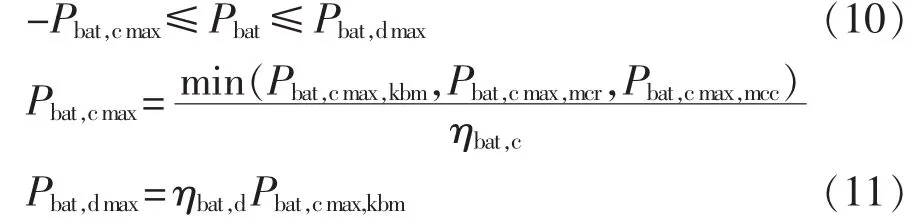
其中，ηbat，c为电池充电效率；ηbat，d为电池放电效率。

此外，还需要考虑蓄电池荷电状态约束：

其中，SOCmax和SOCmin分别表示蓄电池荷电状态的上、下限要求。

1.2.4 发电机模型

通常发电效率随着发电功率的增加有所提高，并在额定负载时达到最大效率。为满足该发电功率输出特性，对发电机模型可进行简化处理，将燃料损耗分为空载损耗和边际运行损耗两部分，用下式表 示[17]：

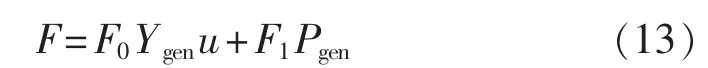
其中，F0为燃料曲线的截距系数（L／（kW·h））；F1为燃料曲线的斜率（L／（kW·h））；Ygen为发电机的额定容量（kW）；Pgen为发电机的输出功率（kW）；u 为发电机开机状态，0表示关机，1表示开机。

发电机满足功率上下限约束：

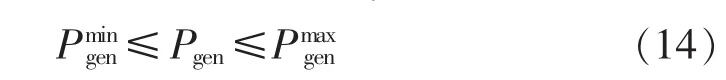
此外，还可根据实际情况增加发电机的最大爬坡率约束、最小开机时间约束等。

1.3 系统运行约束

功率平衡方程是系统运行的主要等式约束条件，要求各时段满足：

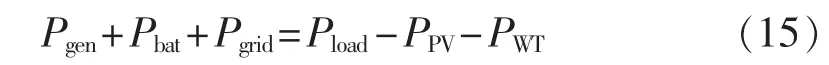
其中，PPV、PWT、Pload分别为光伏、风机和负荷预测功率（kW）；Pbat为蓄电池充放电功率（kW），放电为正，充电为负；Pgrid为微电网和电网之间的交换功率（kW），微电网从电网购电为正，售电为负，且满足式（16）。

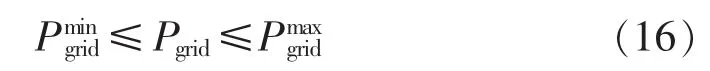
由于微电网的动态优化调度呈现出周期性，通常假设蓄电池SOC在调度时期始末保持一致，即满足约束条件：

其中，SOC0和SOCend分别为调度周期内初始时刻和终止时刻蓄电池的荷电状态。

对系统运行约束的处理方法将在下文中结合优化调度模型进行详细介绍。

此外，主要的运行约束还可包括系统储备容量约束、母线电压和线路潮流约束等。

2 多目标动态优化调度模型

多目标优化模型可以表示为如下一般形式[18]：

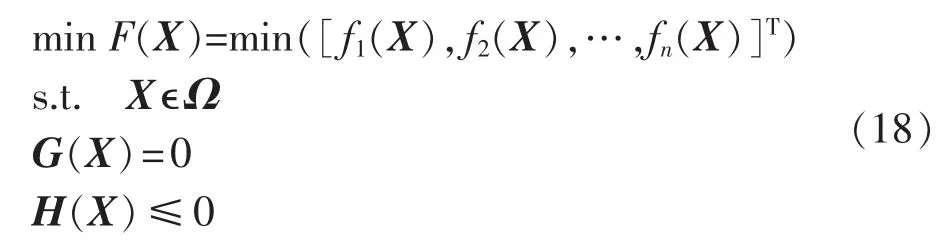
其中，X为优化变量；fi为第i个优化目标；Ω为可行解空间；G和H分别表示等式约束和不等式约束构成的集合。

2.1 目标函数

微电网具有经济、技术、环境等多方面的价值，本文考虑经济和环境双重目标，目标函数如下：

其中，fc为经济目标；fe为环境目标；X为微电网优化调度模型的优化变量，如动态优化调度模型中，可选择调度周期内各时段可调度电源输出功率、储能充放电功率以及电网交换功率作为优化变量。

针对光伏、风机、蓄电池和发电机构成的并网型微电网，本文主要考虑购电成本、设备运行维护成本、燃料成本，同时考虑蓄电池折旧成本[19]，经济成本用下式表示：

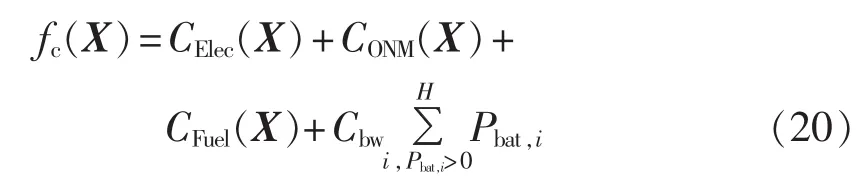
其中，CElec为从电网购电成本（$）；CONM为设备运行维护成本（$）；CFuel为燃料成本（$）；Cbw为蓄电池单位放电折旧成本（$／（kW·h））；Pbat，i表示时段 i蓄电池平均充放电功率（kW），为正表示放电，为负表示充电；H为调度周期内的时段总数。其中，蓄电池单位放电折旧成本采用文献[5]的方法计算。

环境成本主要考虑碳排放以及其他污染气体及颗粒物排放对环境的影响，为反映不同污染排放物的环境影响差异，使用下式计算环境成本[20]：

其中，Ve，i为第 i项污染物的环境价值（$／kg），我国电力工业污染物的环境价值数据见文献[21]；n为污染物种类；Qi（X）为第 i项污染物的排放量（kg）；Vi为排放第i项污染物所受罚款（$），主要污染气体的罚款数量级见文献[22]。

2.2 约束处理方法

根据第1节，仿真模型主要包括2类约束条件，即元件模型约束和系统运行约束。主要的约束处理方法包括硬约束处理方法、柔性约束处理方法和降维处理方法3种，在调度模型中应根据具体情况进行选择，分类说明如下。

a.元件模型约束处理方法。针对仿真模型中的元件模型约束条件，如蓄电池充放电功率限制式（10）、发电机功率约束式（14）等，可采用硬约束的处理方法。这是由于其大多表示设备运行的物理极限，要求强制满足；同时，这些约束通常仅受元件自身当前时刻运行变量影响，通过调整相应运行变量即可满足约束。因此，只要在仿真过程中将违背约束元件的运行变量强制置为满足约束的边界值即可。

特殊地，如果系统中包含发电机爬坡率约束、发电机最小开机时间约束等，需要考虑不同时段的相关性。处理时可将第1个时段作为基准，根据约束条件的边界值逐个调整后续时段的变量数值。

b.系统运行约束处理方法。仿真模型中的系统运行约束通常与多个元件或同一元件多个时段的运行变量相关，具有较强的耦合性。因此，当运行约束违反时难以确定相关变量的调整方式，故而可以采取柔性约束或降维的处理方法。

例如，考虑到蓄电池SOC的时间耦合特性，本文使用柔性约束的处理方式，将其作为惩罚项加入总运行成本，得到计及SOC约束式（17）的目标函数：

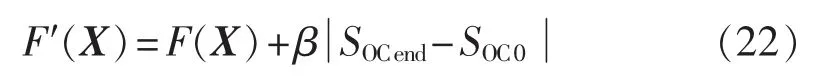
其中，β为SOC约束惩罚因子。

而功率平衡等式运行约束式（15）中则包含了多个元件的运行变量，为此，本文采取了降维方法进行解耦，即假设各变量为不受该等式约束限制的独立变量，仅以其中一个变量作为因变量，其数值由其他变量和等式约束共同确定。如果此时因变量不能满足其元件模型自身约束，则将因变量置为满足约束的边界数值，由此导致的等式约束中的不平衡分量表现为剩余功率或不足功率。当出现剩余功率时，无形中增加了发电成本；当出现不足功率时，则需要在目标函数中增加相应的缺电惩罚成本。但本文重点研究并网型微电网系统，认为电网供电能力充足、缺电率为0，因此在目标函数未计及缺电成本。

3 求解流程

本文以仿真模块和优化模块为核心，求解微电网多目标动态优化调度问题。其中，仿真模块使用第1节介绍的仿真模型和约束条件，结合第2节中约束处理方法，计算得到式（19）中各子目标函数值；优化模块采用文献[23]中的多目标遗传算法NSGA-Ⅱ，该算法基于Pareto分层排序原则对个体进行选择。

结合仿真模块和优化模块，得到微电网多目标动态优化调度的一般流程框图，如图2所示。

图2 多目标动态优化调度流程Fig.2 Flowchart of dynamic multi-objective optimal dispatch

下面详细说明操作流程。

a.数据初始化。输入微电网的系统组成和结构参数、设备模型参数、NSGA-Ⅱ参数。

b.种群初始化。初始种群中的每一个个体对应一个调度周期内的调度方案，这里使用浮点数编码方式，个体可直接由优化变量X表示。

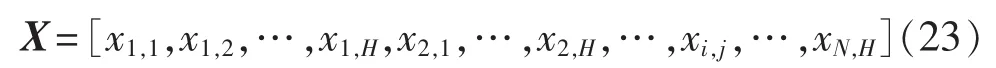
其中，xi，j为设备i在调度周期时段j的调度变量；N为可调度发电设备的总数；H为调度周期内的时段总数。

c.将种群个体作为系统变量输入仿真模块，对违背约束的变量进行修正，并计算系统的经济、环境成本目标值以及惩罚项。

d.将仿真模块的目标值以及惩罚项期望作为输出返回给优化模块，计算个体适应度的数值。这里取考虑惩罚项的目标值作为个体适应度，即：

e.将个体适应度作为优化模型的输入，通过锦标赛选择、单点交叉、均匀变异操作，得到子代种群。

f.重复步骤c和步骤d的操作。

g.对父代种群和子代种群整体进行Pareto分层排序，得到新的种群个体。

Pareto分层排序根据个体的支配关系和聚集距离保留非支配解，为防止NSGA-Ⅱ迭代中出现早熟现象，对排序后的非支配解进行了去重操作，即除去该解集中的重复个体；去重之后，从支配解集中顺序挑选若干层级低、聚集距离大的个体，并添加到新的种群中，以维持种群的规模不变。

h.返回步骤f，直至满足终止条件。本文取终止条件为最大遗传代数，输出最终的优化调度结果，否则返回步骤d。

4 算例分析

以典型的风光蓄柴微电网系统为例，使用本文的多目标优化调度模型进行日前优化调度。系统中包含10 kW风机、300 kWp光伏、200 kW蓄电池、120 kW柴油发电机（以下简称柴发），以及年峰值273 kW的负荷。该系统结构如图3所示。其中，风机、光伏、蓄电池与直流母线相联，柴发、负荷与交流母线相联，直流母线和交流母线通过单向／双向变流器联接，并通过变压器与配电网相联。

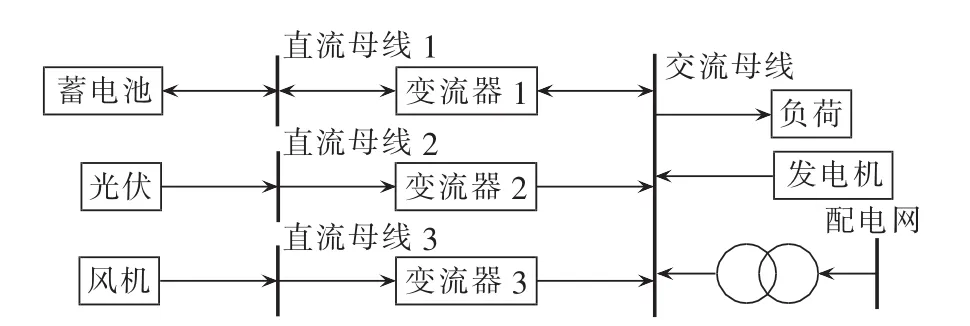
图3 风光蓄柴微电网拓扑结构图Fig.3 Topology of a PV-wind-battery-diesel microgrid

典型日负荷、光照、风速及实时电价数据见表1。

表1 典型日负荷、光照、风速、实时电价数据Tab.1 Data of load，irradiation，wind speed and electricity price for typical day

下面给出模型主要技术参数。光伏参数：功率温度系数-0.5%／℃，降额因数0.9。蓄电池参数：额定电压2 V，额定容量800 A·h，串并联总数288，循环充放电效率0.86，放电 SOC下限 0.4，充电 SOC上限 1，最大充电速率 1 A／（A·h），最大充电电流162 A，最大可能存储能量 551.8 kW·h，速率常数1.101 h-1，容量比0.332。柴油发电机参数：单机额定功率120 kW，最小负荷率30%，燃料曲线截距系数0.08 L／（kW·h），燃料曲线斜率 0.25 L／（kW·h）。 风机参数：单机额定功率10 kW，风机切入风速3 m／s，风机切出风速24 m／s。变流器参数：光伏逆变器效率0.95，风机逆变器效率0.95，蓄电池整流器效率0.95，蓄电池逆变器效率0.95。

设备经济参数如下：燃料费用1.2$／L，发电机启停成本 0，蓄电池折旧成本 0.1$／（kW·h）。

污染物排放参数如表2所示。

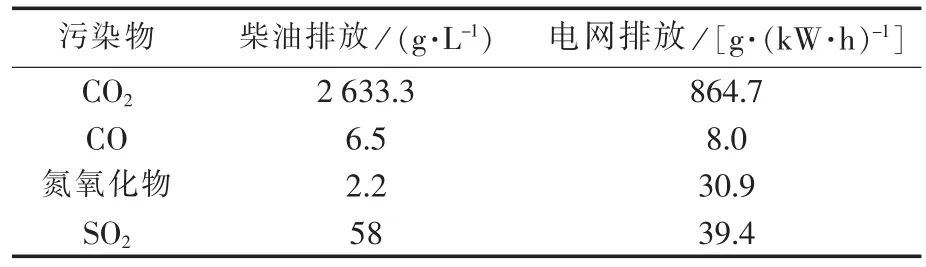
表2 污染物排放参数表Tab.2 Environmental parameter

以风、光、负荷预测数据作为仿真模型的输入，使用多目标优化算法对系统进行日前动态优化调度，优化变量X取为未来24 h各时段蓄电池充放电功率和发电机输出功率：

根据前面介绍的运行约束处理方法，电网的购电或回购电功率Pgrid作为因变量处理，由系统优化变量X和功率平衡方程式（15）共同决定。从电网购电的价格采用上述实时电价[24]，电网回购价格取为0；种群个体数为60，最大遗传代数为500，交叉率为0.9，变异率为0.1。

首先，使用常规的单目标遗传算法求解该动态优化调度问题，分别得到经济和环境目标下的最优调度方案。遗传算法采用轮盘赌选择、单点交叉和变异对种群个体进行优化。

4.1 动态经济调度

以经济成本最低为目标，使用动态经济调度模型，如不考虑蓄电池折旧成本和SOC约束惩罚项，系统的最优经济成本为$48.03；如考虑蓄电池折旧成本和SOC约束惩罚项，系统的最优经济成本为$99.66。在2种条件下，对应的优化调度方案如图4所示。

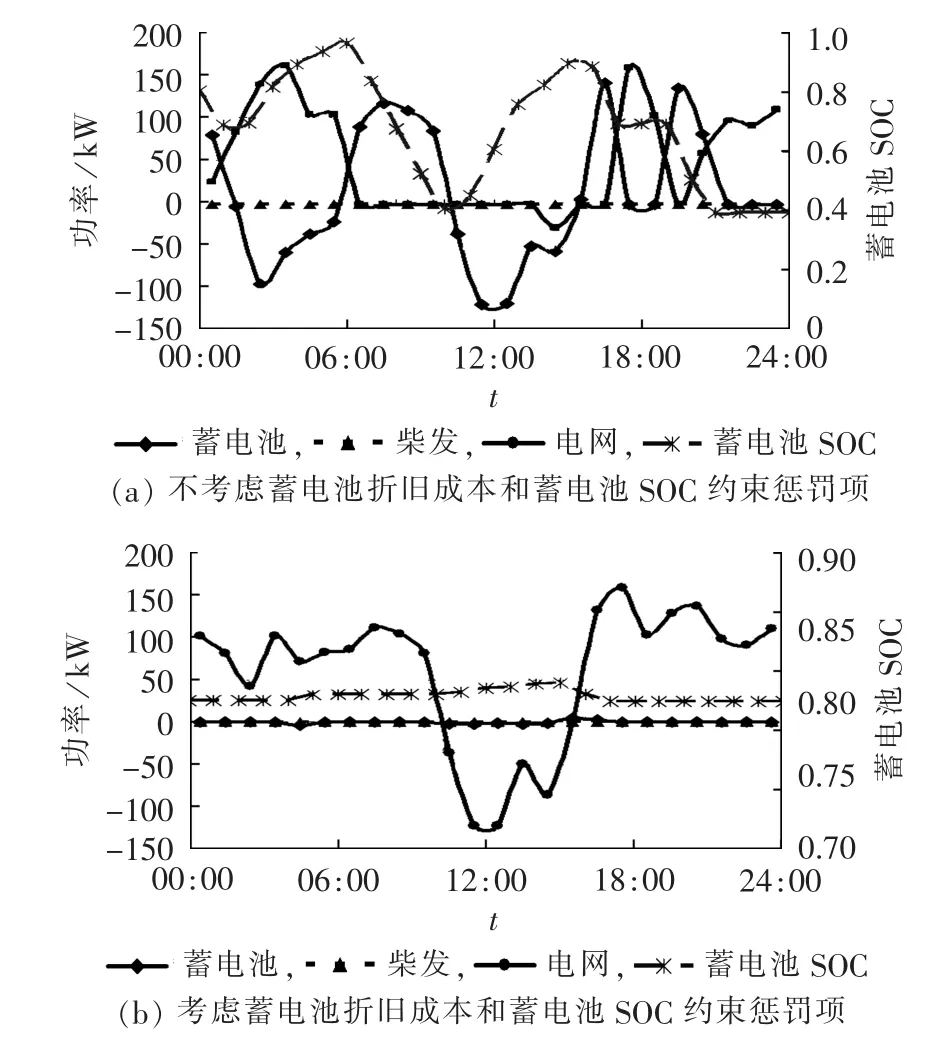
图4 动态经济调度优化结果Fig.4 Results of dynamic economic optimal dispatch

从图4可以看出，由于柴发发电成本较高，柴发在整个调度过程中并不开启。当不考虑蓄电池折旧成本和蓄电池SOC约束时，蓄电池经历了2次主要的充电过程，分别发生在凌晨电价较低的时段和午间光伏发电充足的时段，如图4（a）所示，充分利用了蓄电池的电量转移和存储能力。调度周期结束时，蓄电池SOC降至下限值0.4。当考虑蓄电池折旧成本和蓄电池SOC约束时，由于蓄电池充放电成本较高，几乎不参与系统运行，缺额功率完全由电网提供，如图4（b）所示。调度周期结束时，蓄电池SOC为0.8，与初始值相同。

由于考虑蓄电池折旧成本更接近真实情况，而蓄电池SOC约束可以更有效地维持蓄电池的充放电能力，以下分析计算中均考虑蓄电池折旧成本和蓄电池SOC约束。

4.2 动态环境调度

以环境成本最低为目标，使用动态环境调度模型得到系统的最优环境成本为$48.51，对应的优化调度方案如图5所示。

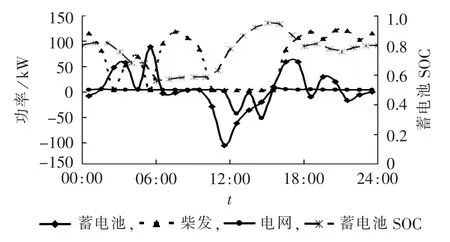
图5 动态环境调度优化结果Fig.5 Results of dynamic environmental optimal dispatch

从图5可以看出，由于柴发发电相对于对电网购电的环境优势，在净负荷较大的时段，柴发提供了主要的缺额功率，电网交换功率基本为零。蓄电池主要在午间吸收剩余的光伏出力，调度周期末蓄电池SOC维持在初始值0.8。

其次，使用基于NSGA-Ⅱ的多目标动态优化算法，得到经济、环境双目标下调度方案的Pareto前沿如图6所示。

图6 多目标动态优化调度的Pareto前沿Fig.6 Pareto front of dynamic multi-objective optimal dispatch

图6中包含了3次独立的测试结果。可见，多目标动态优化得到的Pareto前沿的经济成本分布在[$550，$750]的区间内，环境成本分布在[$60，$100]的区间内，其数值无论从经济成本还是排污水平分析，均远高于相同条件下单目标动态优化调度的结果。分析其主要原因是NSGA-Ⅱ本身在搜索单目标优化结果方面能力较弱，收敛性能较单目标遗传算法差。此外，图6中3次计算得到的Pareto前沿存在较大差距，说明该算法在500代后仍未趋于稳定，算法的收敛性较差。

与单目标优化算法不同，多目标优化算法需要同时考虑2项主要的性能指标——算法的收敛性和解的多样性[23]。最大遗传代数和变异率等算法参数对多目标优化算法性能的影响较大[25]：通常种群代数越大、变异率越高，Pareto前沿越宽，但会相应牺牲计算速度和Pareto前沿的稳定性。

使用本文的多目标改进算法，将上述动态经济调度和动态环境调度的优化结果作为部分初始点，由此得到经济、环境双目标下调度方案的Pareto前沿如图7所示。

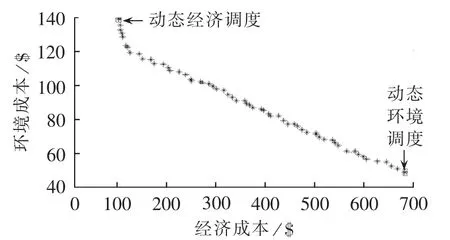
图7 初始点引导的多目标动态优化调度的Pareto前沿Fig.7 Pareto front of dynamic multi-objective optimal dispatch using initial-point-guide

从图7的结果可以看出，在NSGA-Ⅱ中引入初始点引导技术和去重操作，不仅可以获得较为分布广泛而均匀的Pareto前沿，还可以有效弥补该算法收敛性能较差的缺陷，获得更为满意的Pareto边界。

以图7中Pareto前沿中的一个中间点为例，其经济成本和环境成本分别为（$117.36，$122.05），对应的调度方案如图8所示。

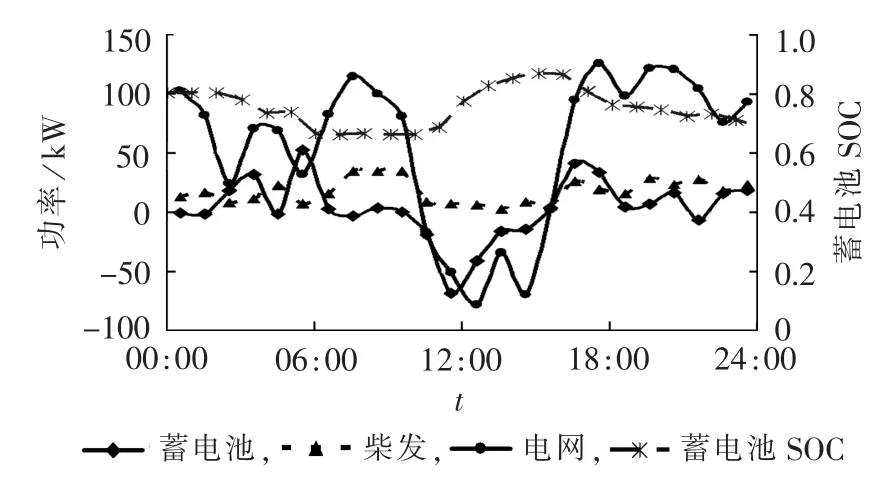
图8 多目标动态优化调度优化结果Fig.8 Results of dynamic multi-objective optimal dispatch

对比动态经济调度、动态环境调度和多目标动态优化的结果，如表3所示。

从表3的结果可以看出，多目标算法可以有效地权衡经济和环境效益，用户可根据自身需求选择更为合理的微电网调度方案。

表3 不同目标下优化结果Tab.3 Results of optimization with different objectives

5 结语

本文为实现微电网系统运行的经济和环境双重优化目标，以独立的系统仿真模块和运行优化模块为核心，建立了微电网多目标动态优化调度的一般模型。以典型的风、光、蓄、柴微电网为例，对单目标的动态经济调度、动态环境调度以及多目标动态优化调度的结果进行了比较，分析了NSGA-Ⅱ在处理多目标动态优化调度中的主要缺陷。在此基础上，对NSGA-Ⅱ进行改进，通过在算法中引入初始点引导技术和去重操作，有效地提高了算法的收敛性能，同时改善了Pareto前沿的分布特性。

此外，仿真模型的拓展以及随机优化方法都可以作为进一步研究的内容。