基于故障支路电流序分量相位关系的选相元件
2013-10-22索南加乐
刘 凯,索南加乐
(1.西安交通大学 电气工程学院,陕西 西安 710049;2.东方电子股份有限公司,山东 烟台 264001)
0 引言
分相电流差动保护原理简单、灵敏度高,适用于系统振荡、非全相等各种复杂的运行状态和各种拓扑结构的电力网络,具有天然的选相能力。由于具有上述优点,线路光纤电流差动保护已广泛应用于电力系统中。
线路相电流差动保护本身有选相能力,不需额外配备选相元件,但相电流差动保护受线路分布电容电流的影响,对于超高压长线路,影响更大。为了消除线路分布电容电流对相电流差动保护的影响,大量的文献研究了差动保护的电容电流补偿方法和不受分布电容影响的纵联保护新原理[1-8]。提高灵敏度的另外一个方法是采用故障分量差动保护原理,同属利用故障分量的零序电流差动保护和负序电流差动保护也在线路上得到了广泛应用[9-10]。零序电流差动保护和负序电流差动保护本身不具备选相能力,需要配置选相元件,以达到选相跳闸的目的。
选相是纵联方向保护、纵联距离保护和后备距离保护的必备功能,因此选相元件一直是线路保护研究中的重点内容[9-16]。文献[13]介绍了利用负序和零序分量之间的相位选相的方法,这种选相方法一般需要和测量阻抗相结合,计算较复杂,且在系统振荡时会遇到困难。利用故障分量正序电流和负序电流之间的相位可以选出各种故障相别,但由于使用故障分量,仅能短时应用[17]。目前常用的选相元件主要有突变量选相和序分量选相2种,但其选相元件都受到系统中电流分布系数大小的影响[15]。
线路差动保护可获得线路两端电气量,因此有更多的信息可用于选择故障相别并具备更好的性能。需要指出的是,在线路差动保护中使用零序和负序电流差动保护的目的是提高灵敏度,零序和负序电流差动保护原理本身受线路分布电容电流的影响也较小,用于二者的选相元件必须考虑分布电容电流的影响,否则,零序和负序差动保护的灵敏度会受其选相元件影响。
文献[9]提出了一种利用故障时三相差流幅值之间的大小关系来选择故障相别的选相元件,该元件未考虑线路分布电容电流的影响;对于分布电容电流大的线路,由于三相差电流中包含电容电流,三相差电流之间幅值比较的结果会受到电容电流的影响,用于高压长线路时难以正确选相。文献[10]提出了基于零序、负序差电流大小和各相差电流大小之间关系的选相元件,该选相元件同样未考虑分布电容电流的影响。
本文对不受线路分布电容电流影响的用于零序、负序差动保护的选相方法进行了研究,提出了基于故障支路电流序分量相位的选相元件。差电流中的负序分量与故障支路的负序电流的相位相同;差电流中的正序分量由故障支路的正序电势和系统电源共同产生;在正序差电流中减去由系统电源产生的正序差电流,修正后的正序差电流与故障支路的正序电流相位相同。负序差电流和修正后的正序差电流分别与故障支路的负序电流和正序电流具有相同的相位,不同的故障类型相位不同,据此可判断故障相别。基于故障支路电流序分量相位的选相元件不受线路分布电容、线路补偿电抗器的投切状态及参数变化的影响,适用于弱馈及单端电源线路。该元件实质上利用了差电流中的正序故障分量和负序分量,但可长期使用。本文用EMTP建立了1000 kV、600 km线路模型,对基于故障支路电流序分量相位关系的选相元件进行了仿真,仿真结果证明了所提方法的有效性。
1 基于故障分量正序电流和负序电流的选相元件[17]
a.单相故障(AG、BG、CG)。
单相故障时,特殊相的正序、负序和零序电流相等,如发生A相接地故障时,ΔI1a=I2a=I0a,故障分量正序、负序电流间的相位差 δ=arg(ΔI1a/I2a)=0°;发生B相接地故障时δ=-120°;发生C相接地故障时δ=120°。
b.相间故障(BC、AC、AB)。
发生BC相间短路故障时,ΔI1a=-I2a,故障分量正序、负序电流间的相位差 δ=arg(ΔI1a/I2a)=180°;发生AC相间短路故障时δ=60°;发生AB相间短路故障时 δ=-60°。
c.发生相间接地故障(ACG、ABG、BCG)。
故障分量正序和负序电流之间的相位关系同b。
图1表示各种不对称故障情况下故障分量正序电流和负序电流之间的相位关系,基于故障分量正序电流和负序电流之间相位关系的选相元件根据此特征来判断故障相别。
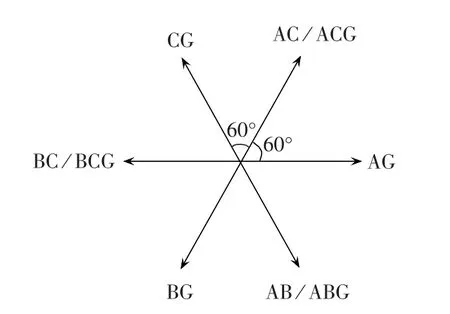
图1 不同故障类型对应的δFig.1 δ of different fault types
2 差电流中正序和负序分量的提取
图2为双电源供电的系统模型,图中,Em、En分别为线路两侧(m、n 侧)电源电势,Um、Un和 Im、In分别为线路两侧的电压和电流,Zms、Zns分别为线路两侧系统阻抗,Zlm、Zln分别为故障点两侧的线路阻抗,IF为故障支路电流,RF为过渡电阻。
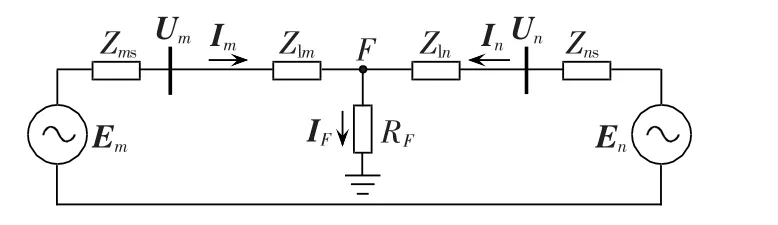
图2 系统模型Fig.2 System model
差电流中的正序和负序分量为:
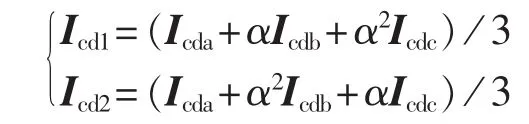
其中,Icd1和 Icd2分别为正序、负序差电流;Icda、Icdb和Icdc分别为三相差电流;α=ej120°。
由图2可知,线路差电流为:
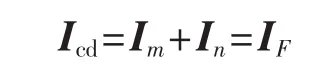
即差电流为故障支路的电流,三相差电流分别为三相流入故障点的电流,正序差电流、负序差电流分别和故障支路的正序电流、负序电流相等。可见,从三相差电流中可提取出故障支路的正序、负序电流,且可长期提取。
3 电容电流对差电流序分量相位的影响
第2节的分析未讨论线路分布电容对差电流序分量的影响。本节首先讨论线路分布电容对负序差电流的影响,然后讨论线路分布电容对正序差电流的影响。
3.1 电容电流对负序差电流相位的影响
图3为线路上发生故障时的负序分量网络图。图中,Um2、Un2和 Im2、In2分别为线路两侧的负序电压和电流,Zms2、Zns2分别为线路两侧系统负序阻抗,Zlm2、Zln2分别为故障点两侧的线路负序阻抗,UF2和IF2分别为故障支路的负序电势和电流。线路采用Π模型,ZC2为线路等效容抗,ICm2和ICn2分别为流过线路两端电容的电流。
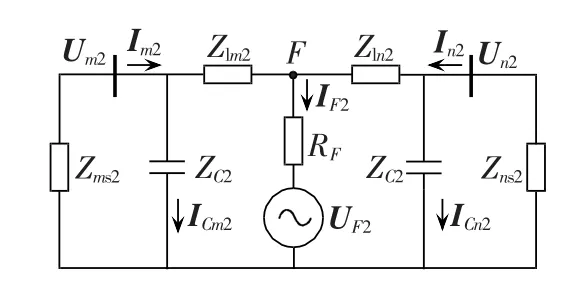
图3 负序网络图Fig.3 Negative sequence network
从图3可知,负序差电流Icd2为:
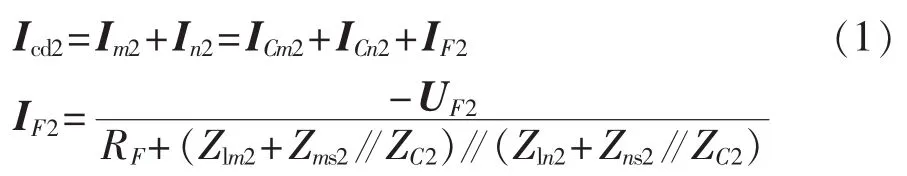
系统阻抗Zms2和Zns2一般为几十欧姆,而线路负序容抗的数量级为千欧姆[6],即 Zms2≪ ZC2、Zns2≪ ZC2,负序容抗对IF2的影响可忽略,IF2可写为:
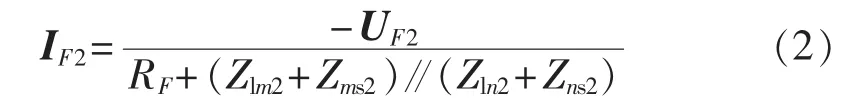
流过线路分布电容的负序电流为:
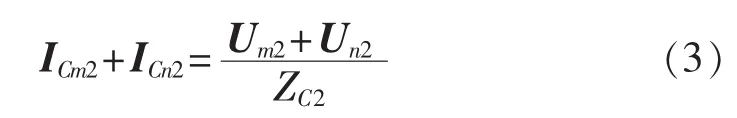
由于线路容抗远大于线路阻抗和系统阻抗,而Um2+Un2<2UF2,可知 IF2≫ICm2+ICn2,结合式(1)可知Icd2和IF2的相位相同,即线路负序差电流和故障支路的负序差电流的相位相同,二者的相位关系不受线路分布电容的影响。
3.2 电容电流对正序差电流相位的影响
图4(a)为线路上发生故障时的正序网络图,根据叠加定理,该网络可分解为故障前网络(图4(b))和故障附加网络(图 4(c))。
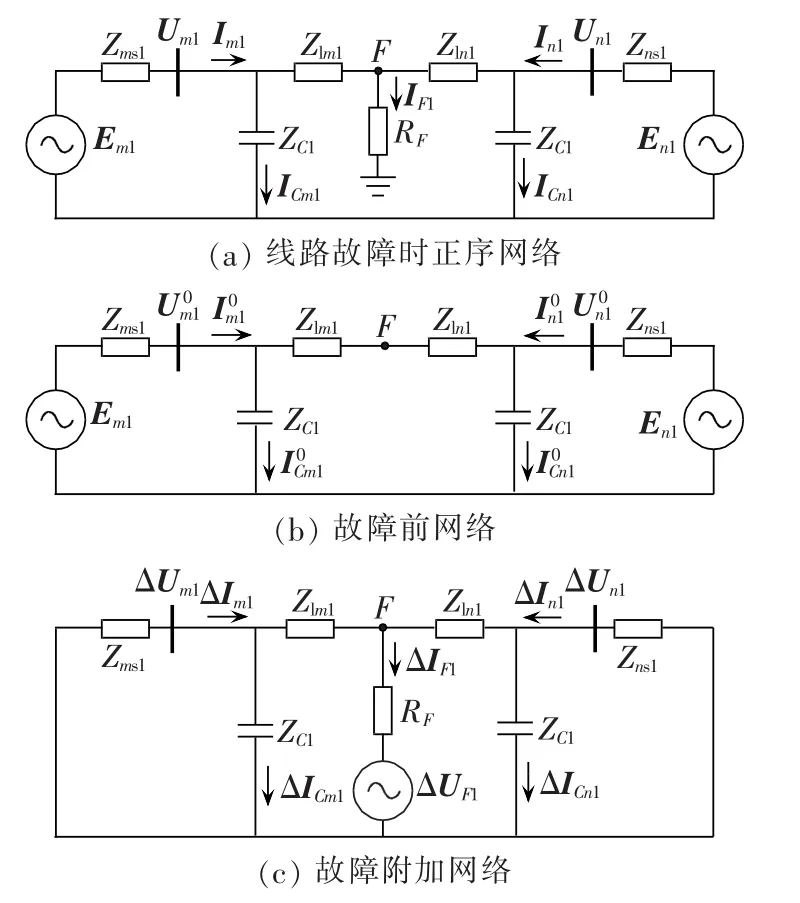
图4 线路故障时的正序网络图Fig.4 Positive sequence network during line fault
从图4(a)可知,故障时的正序差电流为:
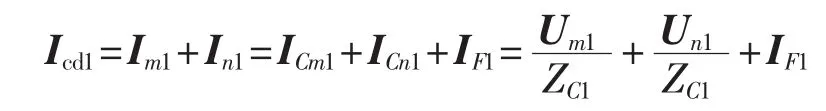
其中,Icd1为故障时的正序差电流,可分解为由系统电源产生的流过线路分布电容的差电流I0cd1和由故障支路的正序电势产生的差动电流ΔIcd1。
由图4(b)可知,由系统电源产生的正序差电流为:
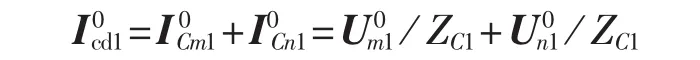
由图4(c)可知,故障支路电势ΔUF1产生的差电流为:
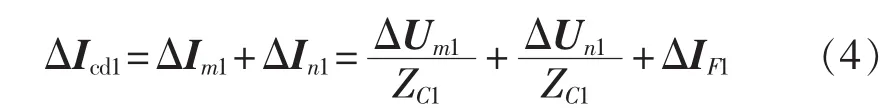
其中,ΔIF1=IF1。 式(4)可写为:
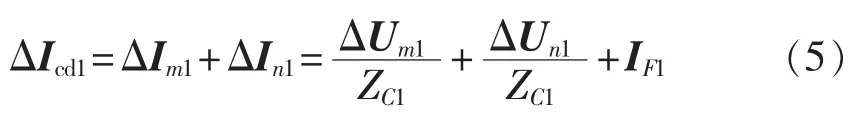
类似于2.1节的分析,可得出正序故障分量差电流ΔIcd1和故障支路正序电流IF1的相位相同,不受线路分布电容的影响。
由于保护得到的是线路两端电流Im1和In1,计算的正序差电流Icd1受系统电源产生的电容电流的影响,在发生高阻故障时,相对于故障支路的电流,系统电源产生的电容电流数值相对较大,正序差电流Icd1和故障支路正序电流IF1的相位可能不一致。
由叠加定理可知Icd1=Ic0d1+ΔIcd1,所以ΔIcd1=Icd1-Ic0d1。如果在正序差电流Icd1中减去系统电源产生的正序电容电流Ic0d1,则可得到ΔIcd1,用其和负序差流比相可以得到可靠的选相结果。
计算Ic0d1时要使用故障前电压Um01和Un01,一种方法是采用记忆法,利用故障前的数据进行计算,但这种方法仅能短时使用。考虑到本选相元件仅用于不对称故障的判别,在发生不对称故障时,线路两端的正序电压和故障前的正序电压在相位上差别不大,尤其是当发生高阻故障时,二者在数值上的差别也比较小。本文采用故障后线路两端的实时正序电压Um1和Un1来代替故障前电压U0m1和 U0n1,从第5节仿真结果可知,这种替代即使在单相接地过渡电阻达900 Ω时也不会导致错误的选相结果。
3.3 基于故障支路电流序分量的选相流程
由3.1节和3.2节的分析可知,负序差电流、修正后的正序差电流和故障支路的正序、负序电流具备相同的相位,可以根据正序、负序电流之间的相位关系利用图1所示的各种不对称故障时的相位特征来选择故障相,本文称利用此方法选相的元件为基于故障支路电流序分量相位的选相元件。
基于故障支路电流序分量相位的选相流程如图5所示。首先采集线路两端三相电流并计算差电流;然后计算差电流中的负序分量和正序分量,并在正序差电流中减去系统电源产生的电容电流;根据负序差电流和修正后的正序差电流之间的相位差δ利用图1所示的故障时故障分量正序电流和负序电流之间的相位关系来判断故障相别。
4 性能分析
4.1 不受分布电容电流的影响
文献[9]提出的利用三相差流之间幅值的大小关系来选择故障相的方法,不适用于超高压长线路。例如,在高压长线上发生单相高阻接地故障时,故障相差电流和健全相差电流在数值上的差别不大,该方法不能正确选相,这在第5节的仿真中得到了验证。
基于故障支路正序电流和负序电流之间相位的选相元件,不受线路分布电容的影响。如3.1节和3.2节所分析,用于选相的负序差电流和修正后的正序差电流分别与故障支路的负序电流和正序电流的相位相同,该特征不受线路分布电容大小的影响。
4.2 受线路补偿电抗器的影响小
基于故障支路正序电流和负序电流之间相位的选相元件,不受线路补偿电抗器的影响。图6为在带电抗器的线路上发生内部故障时的负序网络图,其中,ZL2为线路补偿电抗器的阻抗。
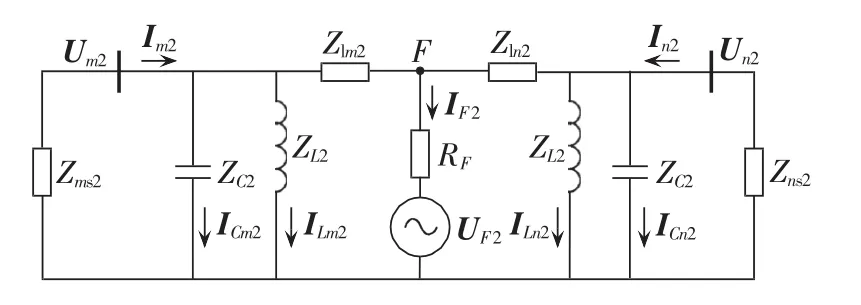
图6 带电抗器的线路内部故障时的负序网络Fig.6 Negative sequence network during internal fault of line with reactors
由图6可知,负序差电流Icd2为:
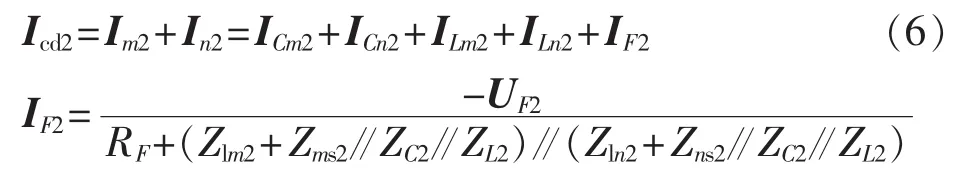
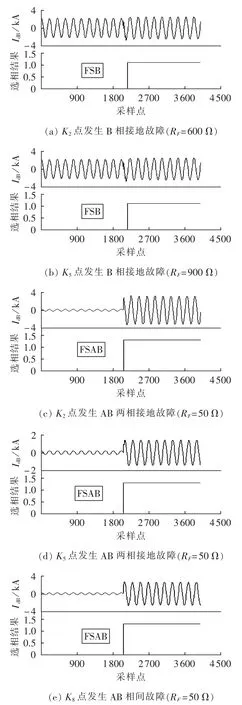
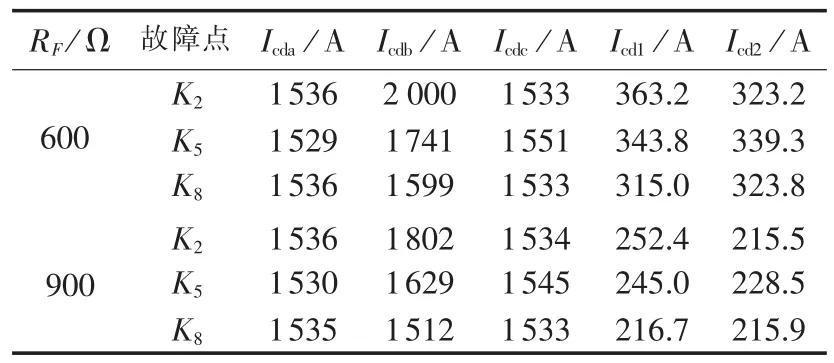
由于线路通常使用欠补偿,所以电抗器的阻抗比线路容抗大(ZL2>ZC2),二者数量级为千欧姆[16];而系统阻抗Zms2和Zns2一般为几十欧姆,即Zms2≪ZC2 流过线路分布电容和补偿电抗器的负序电流为: 由于线路容抗远大于线路阻抗和系统阻抗,可知 IF2>ICm2+ICn2+ILm2+ILn2,结合式(6)可知 Icd2和 IF2的相位相同,即负序差电流和故障支路负序电流的相位是相同的,二者的相位关系不受线路分布电容和电抗器的影响。通过类似的分析可知,修正后的正序差电流和故障支路的正序电流的相位是相同。所以,基于故障支路电流序分量相位的选相元件不受电抗器的影响。 第1节所介绍的基于故障分量正序电流和负序电流之间相位差的选相元件[17]使用单端量实现,其选相结果和纵联方向保护、纵联距离保护、后备距离保护配合使用。该元件因使用故障分量,所以只能短时应用。另外该方法受系统电流分布系数的影响,如果保护所在处分配到的故障分量正序电流或负序电流较小,可能导致无法正确比相(一般当线路较长、或某端系统阻抗较大如弱馈系统或单端电源线路时,会发生这种情况)。 对于带并联电抗器的线路,在修正正序差电流时,除在正序差电流中减去系统电源产生的电容电流外,还需在正序差电流中减去系统电源产生的流过电抗器的电流。通过类似的分析可知,修正后的正序差流和故障支路的正序电流在相位上是相同的。综合以上分析可见,基于故障支路电流序分量相位的选相元件受电抗器的影响较小。 基于故障支路电流序分量相位的选相元件,灵敏度高。第5节的仿真分析中,对于1000kV、600km线路,在发生经900 Ω过渡电阻的单相接地故障时,计算所得负序差电流为240 A左右,故障分量正序差电流为220 A左右,对于微机保护而言,这样大的电流足以保证选相精度。第1节所述的基于故障分量正序电流和负序电流相位差的选相元件,受电流分布系数影响,线路某侧分配到的故障分量正序电流和负序电流可能较小,在这种情况下难以准确选相。文献[9]所提的基于差电流幅值的选相元件在这种情况下也不能正确工作,此时故障相差电流约为1 800 A,健全相差电流为1 500 A左右,故障相和健全相的差电流相差不大,该元件不能正确选相。 采用图7所示模型对基于故障支路电流序分量相位的选相元件进行了仿真验证。图7为EMTP仿真模型,电压等级为1 000 kV,线路采用分布参数模型,线路长度为600 km,两侧电源的正序和零序系统阻抗分别为:Zm1=Zn1=(0.4+j4.9)Ω,Zm0=Zn0=(0.1+j1.7)Ω,其中 Zm1、Zn1和 Zm0、Zn0分别为 m、n 侧系统正序阻抗和零序阻抗。模型中的线路参数为:正序参数 r1=0.01958 Ω/km,l1=0.8192 mH/km,c1=0.013 5 μF/km;零序参数 r0=0.1828 Ω/km,l0=2.74 mH/km,c0=0.0092 μF/km。 仿真中,分别在 K2、K5、K83 个点模拟各种金属性故障和各种高阻接地故障。K2、K8分别位于m、n端线路出口,K5位于线路中点,计算时采用傅里叶算法。 图7 仿真模型图Fig.7 Simulation model of system 图8为部分仿真结果。图8的各子图中上图为B相差动电流波形,FSB表示选相结果为B相,FSAB表示选相结果为AB相间故障或AB相间接地故障。从图中可以看出,在发生故障后,基于故障支路电流序分量的选相元件快速、正确地选出了故障相别。本文对各种故障类型和经不同数值的过渡电阻故障的情况进行了大量的仿真,基于故障支路电流序分量的选相元件均能正确选择故障相别,为节省篇幅,未列出具体结果。 为和文献[9]所提的基于差电流幅值的选相元件进行对比,表1中列出了在K2、K5和K83个点分别经600 Ω和900 Ω过渡电阻接地故障时的三相差电流Icda、Icdb和Icdc、负序差电流Icd2和修正后的正序差电流Icd1。 文献[9]中提出的选相元件简述如下: a.将三相差电流进行排序,表示为Icdmax≥Icdmid≥Icdmin,Icdmax为最大相差电流,Icdmid为中间相差电流,Icdmin为最小相差电流。 b.如果Icdmax≥kIcdmin,则差电流最大相为故障相;如果同时满足Icdmid≥kIcdmin和Icdmax≤kIcdmid,则差电流中间相也为故障相;k取值为1.5~2。 从表1可以看出,在发生故障时,故障相的差电流约为健全相的1.3倍,不满足Icdmax≥1.5 Icdmin的关系,该选相元件不能正确工作。而此时,负序差电流和修正后的正序差电流为200~300 A,微机保护精度较高,在这种情况下,仍能准确分辨二者相位,选出故障相别。 图8 选相结果Fig.8 Results of phase selection 表1 故障时的差电流Tab.1 Differential current during line fault 本文对不受线路分布电容电流影响的用于零序、负序差动保护的选相方法进行了研究,提出了基于故障支路电流序分量相位的选相元件。差电流中的负序分量,包含故障支路中的负序电流及流过线路分布电容的负序电流,完全由故障支路的负序电势产生。差电流中的正序分量,由故障支路的正序电势和系统电源共同产生;通过在正序差电流中减去由系统电源产生的正序差电流,剩余正序差电流完全由故障支路的正序电势产生,包括流过故障支路的正序电流和流过线路分布电容的正序电流。负序差电流和修正后的正序差电流分别与故障支路的负序电流和正序电流具有相同的相位,据此可以判断故障相别。所提选相方法不受线路分布电容的影响,不受线路补偿电抗器的投切状态及参数变化的影响,适用于弱馈及单端电源线路,灵敏度高。该元件实质上利用了差电流中的正序故障分量和负序分量,但是可以长期使用。用ATP建立了1 000 kV、600 km线路模型,对新的选相元件进行了仿真,仿真结果表明,单相接地故障时即使过渡电阻达到900 Ω,该选相元件也可以正确选相,证明了新方法的有效性。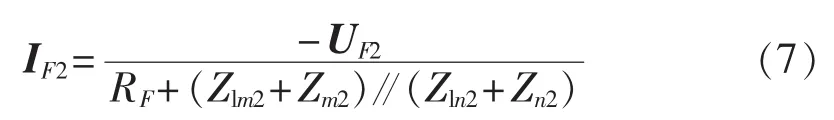
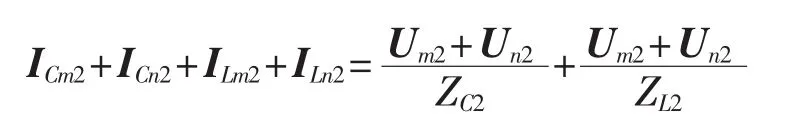
4.3 可长期使用,不受电流分布系数的影响,适用于弱馈线路
4.4 灵敏度高
5 仿真验证

6 结论
