一种计算电压稳定边界的两阶段潮流方法
2013-10-22牟晓明李志民
牟晓明,李志民
(哈尔滨工业大学 电气工程系,黑龙江 哈尔滨 150001)
0 引言
近年来由于电压稳定事故的频繁发生及各种间歇式能源的大规模并网,使得电力系统的静态电压稳定问题受到了学术界及电网运行和规划部门的高度关注。静态电压稳定分析是电力系统运行和规划中的重要工作之一,对电力系统的安全运行具有重要意义。
目前为止,静态电压稳定分析方法主要包括奇异值(特征值)分解法[1-2]、直接法[3-5]、戴维南等值法[6-9]、连续潮流法[10-18]、最优潮流法[19-20]、混合法[21-23]等。其中,基于连续潮流的P-U(Q-U)曲线法,由于能给出电压稳定裕度信息,且能模拟系统在过渡过程中的各种物理约束、发电机有功分配、负荷增长方式等因素,并能克服潮流在临界点的发散问题,因而被广泛应用于工业实践。但如何进行步长控制是连续潮流计算中的一个关键环节[24]。选择一个恒定的小步长可以获得较精确的解,但是小步长会导致多次的潮流计算;较大的步长会引起预测点与实际点的较大偏离,从而增加校正过程的计算时间。
研究表明,将常规潮流与连续潮流相结合,可以达到快速、准确计算电压稳定边界的目的。首先从基本工况逐步增加负荷,利用潮流求解方法,跟踪计算至崩溃点附近;然后利用连续潮流跟踪计算至崩溃点。但在常规潮流计算阶段,如何设计一个有效的步长增长策略,是一个需要考虑和解决的重要问题。
文献[25]基于网络等值和阻抗匹配概念,建立了一个用于确定步长增长的阻抗比指标及相应的电压稳定边界计算方法。研究表明,该方法可以快速地将系统运行状态计算至崩溃点附近;但在临近崩溃点处,该方法有时会失去作用。基于文献[25]的成果及存在的问题,本文提出一种近似用于描述系统电压稳定性的特征指标及计算电压稳定边界的两阶段混合潮流算法。
本文方法将电压稳定边界的计算过程分成2个阶段:在阶段1中,利用提出的电压稳定指标及二分法原理,确定常规潮流计算阶段中的功率增长步长,快速求出系统的近似电压稳定边界;在阶段2中,采用连续潮流方法,对电压稳定边界进行精确计算。在整个计算过程中,可以通过提出的电压稳定指标识别当前系统是否已经接近于极限运行状态,以及是否需要进行阶段1和阶段2的更换。
1 一种近似描述系统电压稳定性的解析指标
由电路理论可知,对于任一包含n个负荷节点的电力网络,均可以写出负荷节点电压方程:
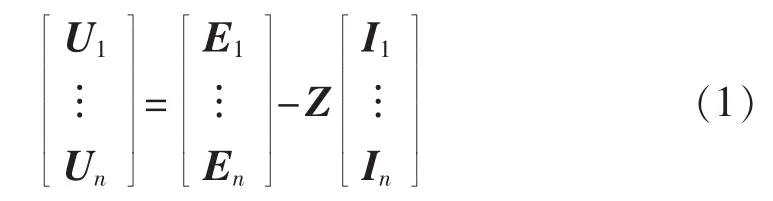
其中,Ui和Ii分别为负荷节点i的电压和电流相量,Z为收缩到负荷节点的系统网络阻抗矩阵,Ei为各负荷节点均开路时负荷节点i的电压相量。
以负荷节点i为例,可以写出下面的等值方程:
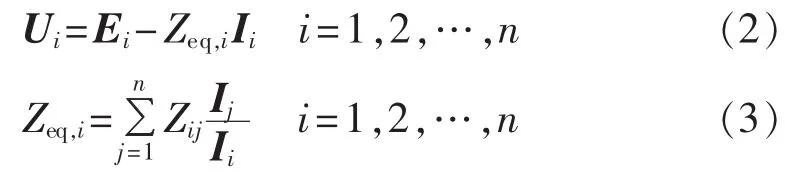
其中,Zeq,i为与负荷节点 i对应的等值阻抗;Zij为矩阵Z的第i行第j列元素。
研究表明,在最大传输功率条件下,各负荷阻抗Zi与相应等值阻抗Zeq,i满足一种特殊的阻抗匹配条件:
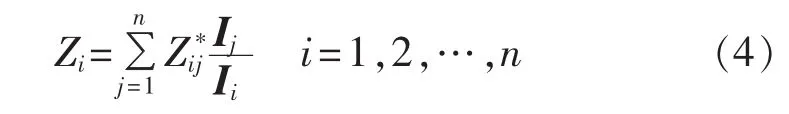
尽管实际电力系统不可能运行在式(4)所描述的阻抗匹配条件下,但这一阻抗匹配形式仍具有一定的理论意义和应用价值。本文试图研究如何利用该等值阻抗进行电压稳定边界求解过程中的步长控制,定义了如式(5)所示的特征指标:
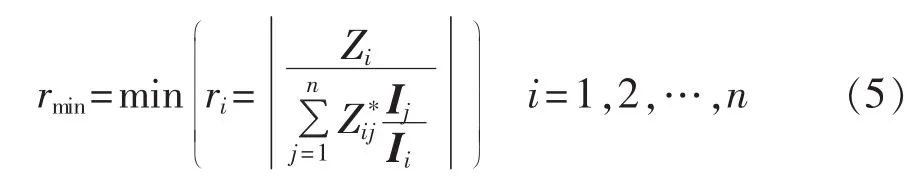
在实际电网量测系统和潮流计算结果中,一般仅给出节点电压和电流相量信息,而式(5)中并不显示与电压稳定有直接关系的节点电压量测信息。因此,对式(5)进行变换是很有必要的。本文给出了式(5)的另一种表达形式,如式(6)所示:
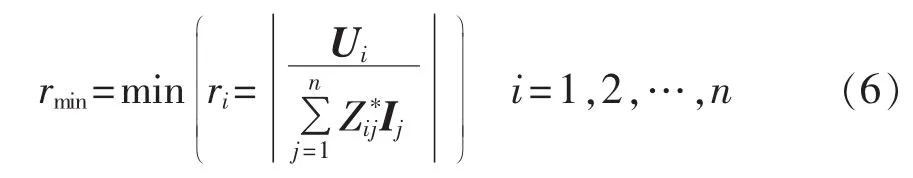
其中,ri为负荷节点电压与所有负荷电流在相应网络阻抗上引起的累积电压降的比值,Ui为负荷节点i的电压。指标rmin可以近似地用于描述系统的电压稳定性。
为了研究指标rmin所具有的特性,已经做了大量的算例仿真与分析。图1和图2分别给出了IEEE 30节点系统和Polish 2 746节点系统的仿真结果(系统结构图和基态潮流数据见文献[26])。在仿真计算中,所有负荷被假设为恒功率负荷,且以一个共同的比例因子增加。所有负荷节点的电压和电流信息均由MATPOWER程序计算得出。
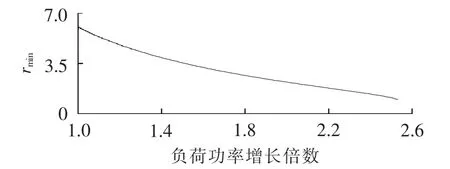
图1 不同负荷条件下IEEE 30节点系统的指标rminFig.1 Index rminof IEEE 30-bus system for different load conditions
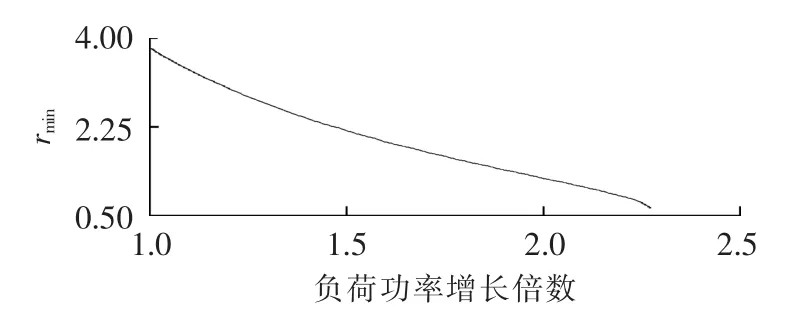
图2 不同负荷条件下Polish 2746节点系统的指标rminFig.2 Index rminof Polish 2746-bus system for different load conditions
从图1和图2可以看出,当系统负荷较轻时,式(6)的分子较大、分母较小,指标rmin较大。随着系统负荷的增加,式(6)的分子会逐渐减小,而分母逐渐变大,因此指标rmin呈下降趋势。在崩溃点附近,rmin通常会小于1,且下降速度相对较快。当运行点离崩溃点较远时,指标rmin通常会大于系统负荷所能增加的最大增长倍数的2倍。
应该指出的是,式(3)中的等值阻抗并不是戴维南等值阻抗,它将系统中其他所有负荷对被等值电路的影响都作用于等值阻抗,本质上这些影响应该既作用于等值阻抗也作用于等值电势。因此,式(3)的等值阻抗会比真实的戴维南等值阻抗大。这也从理论上解释了为何rmin在崩溃点附近通常会小于1。
2 两阶段电压稳定边界计算方法
尽管指标rmin可以近似地用于描述系统的电压稳定性,但该指标不能提供电力系统运行人员所熟知和关注的功率裕度信息,因而不便于被电力工程人员所采用。指标rmin的优点在于其解析性,不需要潮流迭代,计算速度快。因此,将其与连续潮流计算方法相结合,用于潮流计算功率增长步长控制,兼顾了二者的优点,具有理论和应用价值。
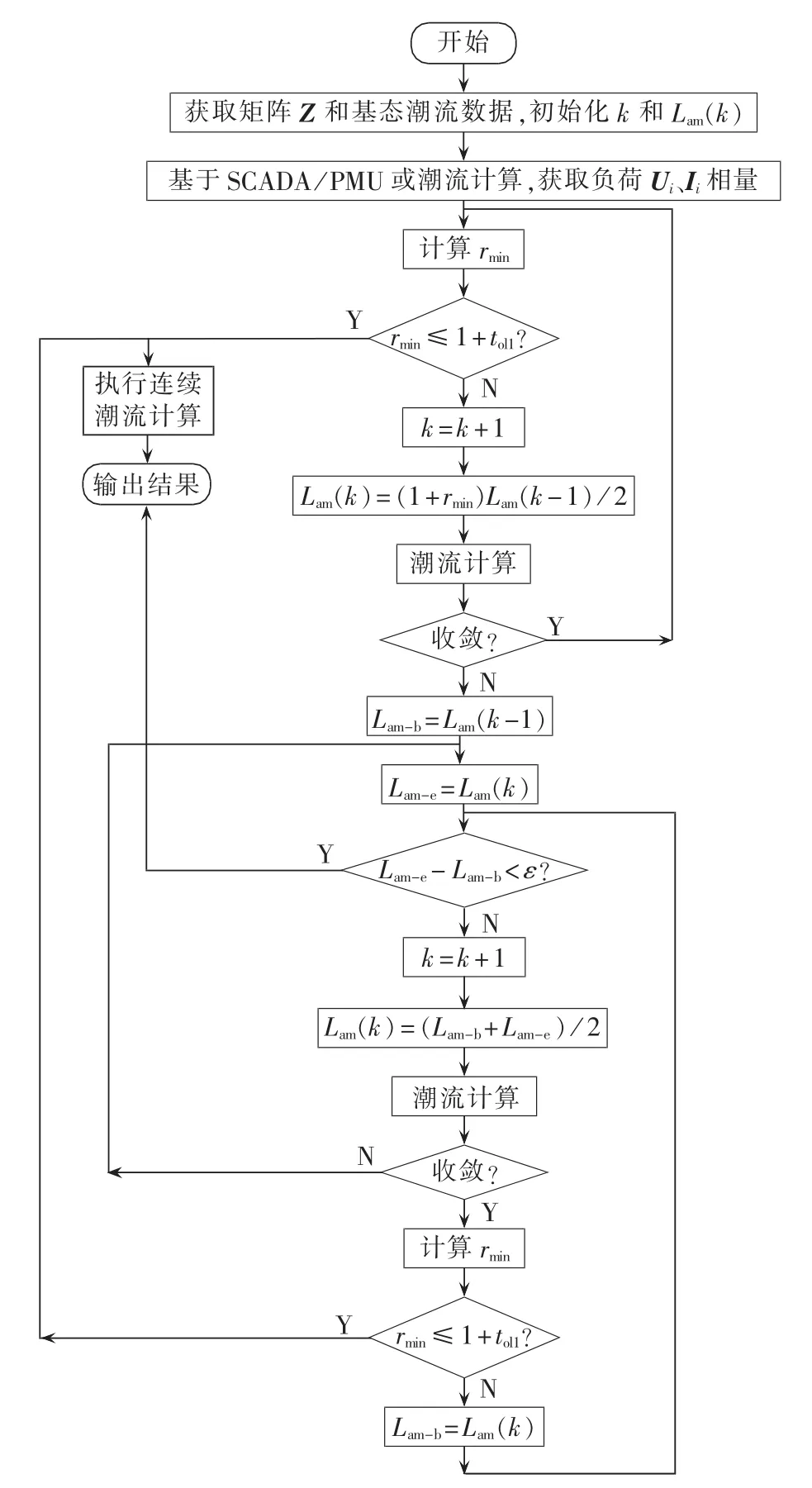
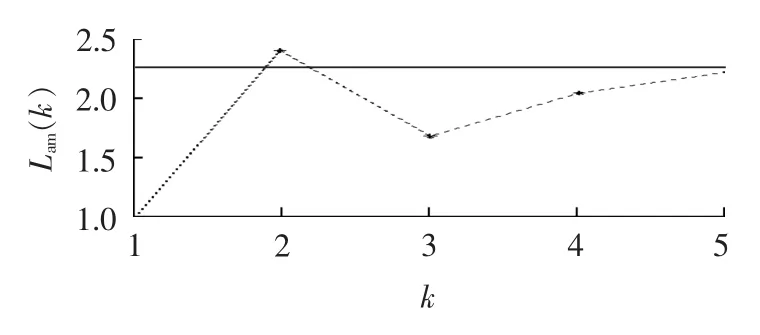
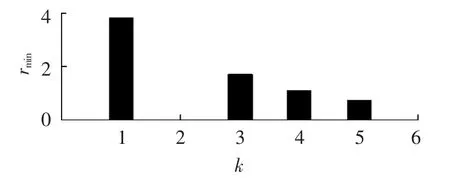
以图3所示的P-U曲线和P-rmin曲线示意图为例,对本文方法进行简要介绍和说明。图中根据rmin的大小,将负荷功率P分成3个区段:区段1中rmin>1+tol1(tol1为一指定的较小值,如1.05等);区段2中1 图3 P-U和P-rmin曲线示意图Fig.3 Schematic diagram of P-U and P-rmincurves 在区段1,如果采用连续潮流或常规重复潮流方法,计算速度可能会比较慢。直观上,在该区段,rmin可以直接选作功率增长步长。然而,由图1和图2的仿真结果可知,当系统远离崩溃点时,rmin作为步长通常会使系统处于崩溃点之外,此时系统潮流不收敛。因此,本文采用以下步长更新方式: 其中,Lam(k)为当前状态的负荷增长因子,k为当前状态。 在实际计算中,式(7)中的 Lam(k+1)仍可能使系统处于崩溃点之外。在这种情况下,本文以Lam(k)为起点、Lam(k+1)为终点,利用二分法回找系统运行点: 在区段2,理论上可以采用区段1的步长更新策略。然而,在该区段,由于通常为非常接近于1的值,所以步长更新可能很慢,会产生多次的潮流计算。因此,当系统运行或迭代计算至区段2时,转换为连续潮流计算通常更为有效。 由以上分析可知,区段2和区段3均采用连续潮流计算方法,所以可以合并为新的区段2。因此,本文提出一个两阶段的混合连续潮流跟踪算法,将电压稳定边界的计算过程分成2个阶段:在阶段1(区段 1),利用式(7)或式(8)中的步长更新策略,快速求出系统的近似电压稳定边界;在阶段2(系统运行或迭代计算至区段2或区段3),采用连续潮流方法,对电压稳定边界进行精确计算。在整个计算过程中,可以通过指标rmin识别系统是否已经接近于极限运行状态,以及是否需要进行阶段1和阶段2的更换。 图4给出了本文方法的计算流程。由图4可以看出,利用本文方法实现电压稳定边界的快速计算,主要包括如下几个步骤。 a.读取负荷阻抗矩阵和潮流计算的基础数据,并初始化参数k和Lam(k)。 b.执行潮流计算,求出各负荷节点的电压和电流相量。 c.计算当前状态下的系统电压稳定指标rmin,这里所述当前状态用负荷增长因子Lam(k)表征,k=1为初始状态,Lam(1)=1。 d.若rmin≤1+tol1,执行连续潮流计算,输出结果,计算结束;否则,令 k=k+1,利用式(7)更新 Lam(k)的值。 e.计算Lam(k)状态下的系统潮流;若潮流收敛,返回步骤 c;否则,令 Lam-e=Lam(k)和 Lam-b=Lam(k-1)(为了编程方便,这里分别用Lam-b和Lam-e表示二分法的起点和终点),执行步骤f。 f.如果Lam-e-Lam-b<ε(ε为判定迭代过程是否中止的判据,取0.001通常可满足要求),则Lam-b为计算结果,计算结束;否则,令k=k+1,利用式(8)所示的二分法更新系统负荷增长因子Lam(k)。 g.计算当前Lam(k)状态下的系统潮流;如果潮流收敛,则执行步骤 h;否则,更新 Lam-e=Lam(k),返回步骤 f。 图4 两阶段电压稳定边界计算流程图Fig.4 Flowchart of two-stage voltage stability margin calculation h.计算指标 rmin;如果 rmin≤1+tol1,执行连续潮流计算,输出结果,计算结束;否则,更新 Lam-b=Lam(k),返回步骤f。 原理上,在步骤h中,可以利用二分法循环迭代,直至系统的电压稳定边界。然而,在进行二分法迭代计算过程中,如果rmin小于事先指定的值(如1.01)之后,执行连续潮流计算通常更有效。 为了验证本文方法用于计算电压稳定边界的有效性,对IEEE 30节点系统、IEEE 118节点系统、Polish 2 746节点系统等各种规模的电力系统进行了仿真和分析。 这里主要对Polish 2 746节点系统的仿真结果进行介绍和分析,迭代计算过程和结果如图5和图6所示。在仿真计算中,各负荷节点的电流和电压数据通过基于MATPOWER的潮流计算程序获得[26]。在图5中,实线(直线)代表利用小步长重复潮流法跟踪计算出来的电压稳定边界(系统最大负荷增长因子),虚线代表利用本文方法的迭代过程和计算结果。可以看出,本文方法只需要5次潮流计算,已经使系统状态足够接近于系统真实的极限运行状态。 图5 Polish 2 746节点系统电压稳定边界仿真结果Fig.5 Simulative results of voltage stability margin for Polish 2 746-bus system 图6 Polish 2 746节点系统每一步迭代计算时的rminFig.6 rminof each iteration calculation for Polish 2 746-bus system 下面对图5和图6中的计算结果作量化分析,以使读者对本文方法有更直观的认识。 首先,计算系统基态潮流(迭代次数k=1),得到指标rmin=3.828。由于此时的rmin远大于1,所以需要更新 k=2,并利用式(7)计算 Lam(2)=2.414。 在Lam(2)=2.414状态下,执行潮流计算,潮流不收敛,则知Lam(2)=2.414已经使系统超出了极限运行状态,因此需要更新k=3,并利用式(8)计算得到Lam(3)=1.707。 在Lam(3)=1.707状态下,执行潮流计算,潮流收敛,计算得到rmin=1.728。由于此时的指标rmin未接近于1,所以需要更新k=4,并利用式(8)计算得到Lam(4)=2.061。 在Lam(4)=2.061状态下,执行潮流计算,潮流收敛,计算得到rmin=1.112。由于此时的指标rmin仍未非常接近于1,所以需要继续更新k=5,并计算得到Lam(5)=2.237。 在Lam(5)=2.237状态下,执行潮流计算,潮流收敛,计算得到rmin=0.758。由于此时的指标rmin已经小于1,表明系统已经接近于极限运行状态,此时调用连续潮流计算程序,即可快速得到系统的电压稳定边界。 事实上,在对计算精度要求不是很高的应用场景下,Lam(5)=2.237这一结果也能满足一些应用要求。这种情况下,无需调用任何连续潮流计算程序,只需通过识别rmin是否小于1,即可判断计算程序是否可以终止,并输出计算结果。 本文提出了一种具有解析性质且能近似用于描述系统电压稳定性的特征指标,及基于这一指标的两阶段电压稳定边界评估方法。仿真结果表明,本文方法可以有效地实现功率步长控制,提高电压稳定边界的计算速度。当系统远离崩溃点时,利用所提出的电压稳定指标及二分法原理,确定重复潮流计算过程中的功率增长步长,快速求出系统的近似电压稳定边界;当系统运行或迭代计算至崩溃点附近时,所提出的电压稳定指标会接近于1,表明此时需要转入阶段2的连续潮流计算。因此,本文方法不仅可以快速计算电压稳定边界,而且在计算过程中可以提供系统是否已经接近于极限运行状态等信息。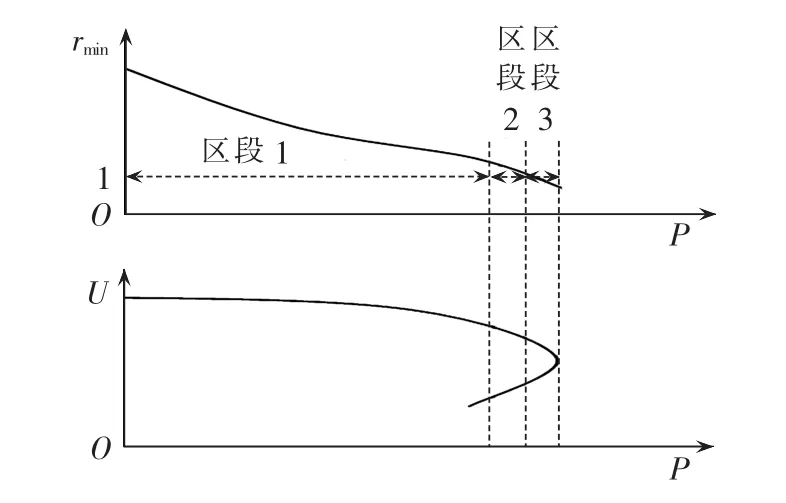
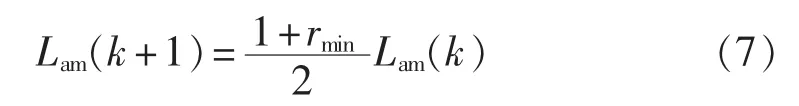
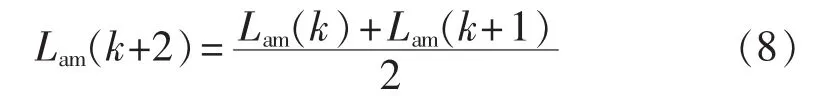
3 计算步骤和流程
4 算例分析
5 结论
