基于故障暂态信号及其衰减特征的配网单相接地故障测距

张文海，肖先勇，汪 颖

（1.四川大学 电气信息学院，四川 成都 610065；2.四川大学 智能电网四川省重点实验室，四川 成都 610065）

0 引言

为了提高供电可靠性，我国6～35 kV配网主要采用中性点非有效接地方式[1]，发生占总故障50%～80%[2]的单相接地故障后，传统故障处理方法通过人工巡线查找故障点，费时耗力，延长了故障停电时间。研究准确有效的单相接地故障定位方法，对于及时排除故障、提高供电可靠性有重要理论价值和现实意义。

现有配网单相接地故障定位有离线法[3-4]和在线法[5-13]。离线法在断电后通过注入信号确定故障位置[3-4]，定位效果好，但需停电和外加设备。在线法根据在线测量值进行定位，又分故障区段定位[5-7]和故障测距[8-10]。前者通过沿线安装测量装置确定故障区段，其成本高；后者通过站端测量值计算故障点与测量点间的距离。文献[9-11]提出用故障稳态特征进行故障测距，但稳态故障电流小，测距误差较大，可靠性低，而暂态特征相对比稳态特征更明显，因此，基于暂态特征的故障测距法引起了广泛关注，并已被用于故障选线[12]。

随着电子式互感器的应用，测量信号可不受铁芯饱和影响，使基于暂态特征的故障测距法成为可能。文献[13]利用暂态行波进行测距，但行波法对装置要求很高，成本大，不利于实际应用；文献[14]利用暂态信号进行小波变换，结合神经网络进行故障测距，但训练样本大，且系统结构变化后需重新训练。文献[15]提出利用小波变换提取充电暂态特征定量计算故障距离，但计算结果易受暂态信号衰减特征影响，尚需进行深入研究。

本文深入研究了配网单相故障充电暂态信号及其衰减特征，在现有暂态特征测距法的基础上，提出一种自适应确定充电暂态信号有效区段的故障测距法。利用快速傅里叶变换FFT（Fast Fourier Transform）法分析故障相暂态信号，判定充电暂态信号的有效性，并确定充电信号频率，再通过时频分析法进一步提取充电暂态信号特征，根据充电暂态信号的幅值衰减特征自适应确定暂态信号的有效区段，利用有效区段内信号进行故障测距。并分别对比研究了采用实小波、复小波和S变换提取充电暂态特征的不同特点，比较了故障距离、故障电阻、故障初相角以及噪声信号对3种方法的影响。算例仿真证明，考虑充电暂态及其衰减特征后，利用S变换法提取特征并进行故障测距的方法，结果更准确，具有可行性。

1 单相接地故障暂态信号及其衰减特征

1.1 故障暂态信号特征

中性点非有效接地系统发生单相金属性接地故障时，故障相电压降到0，非故障相电压升高到正常相电压的倍[16]。 故障暂态信号包括工频分量、对非故障相线路电容的充电暂态信号、故障相线路电容的放电暂态信号，以及消弧线圈中产生的暂态直流分量4个分量[16-17]，且除工频分量外的3个分量均按指数衰减，衰减暂态信号流通路径如图1所示。放电信号由于流通回路电感小，信号衰减快，振荡频率高；而充电信号流通回路电感大，信号衰减慢，振荡频率低，信号幅值大[16]。

图1为含两回出线的配网模型图，假设出线2的c相发生单相接地故障，RF为故障电阻，M点为变电站端测量点，K为中性点接地方式选择开关（闭合时为谐振接地，断开时为不接地）。

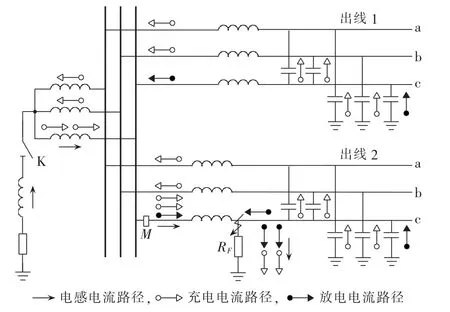
图1 单相接地故障模型Fig.1 Model of single-phase-to-ground fault

1.2 暂态信号衰减特征

以充电暂态信号为例，将信号回路进一步简化可等效为串联RLC电路[15]，据电路理论，当回路参数满足式（1）时，暂态信号为振荡衰减，否则为直流衰减。因此，对于确定的故障点，系统存在临界故障电阻，且该电阻由系统等效参数决定。据统计，中性点不接地系统单相接地故障电阻在40 Ω附近[2]，仿真发现，故障电阻临界值为100 Ω左右（由实际网络参数和故障情况决定），因此，大部分单相接地故障的充电暂态信号都满足振荡衰减。振荡衰减暂态信号如式（2）所示[16-17]，衰减系数如式（3）所示[16]。

其中，R、L、C分别为串联RLC回路的等效电阻、电感和电容，A为暂态信号幅值，δ为暂态信号衰减系数，f为暂态信号频率，θ为其初相角。

由式（3）可见，电阻越大，衰减系数越大，暂态信号衰减越快，持续时间也越短。对于确定的故障点，回路电阻主要由故障电阻决定，因此故障电阻对暂态信号衰减特征影响很大。图2为金属性单相接地故障和故障电阻为40 Ω时故障相电流波形图，可见故障电阻对暂态信号衰减特征有很大影响——故障电阻增大明显导致暂态信号持续时间变短。因此在进行分析时需根据暂态信号的衰减特征自适应确定信号有效区段，以保证信号的合理、充分利用。而故障电压初相角主要影响暂态信号幅值[16]，不会对暂态信号的频率成分以及信号衰减特征产生影响。

2 基于充电暂态信号的测距原理

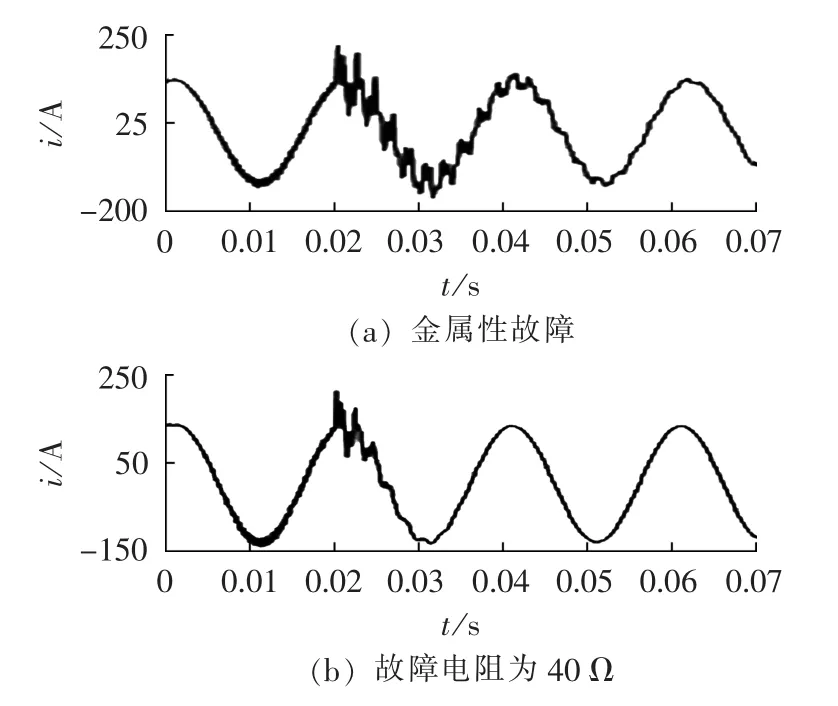
图2 不同故障电阻下的故障相电流波形Fig.2 Current waveforms of faulty phase for different fault resistances

充电暂态特征测距原理可理解为基于高频分量的阻抗法。由于故障时大部分暂态信号均经故障点与地构成流通回路，通过高频分量定量计算可计算出故障距离，原理如图3所示。该方法利用了单相接地故障暂态分量幅值大且不受消弧线圈影响的优点；由于无需采用工频分量，从原理上避免了负荷电流和系统不平衡影响；当线路通过高频分量时，线路的电抗更大，可更有效减小故障电阻的影响，提高计算的准确性和可靠性。

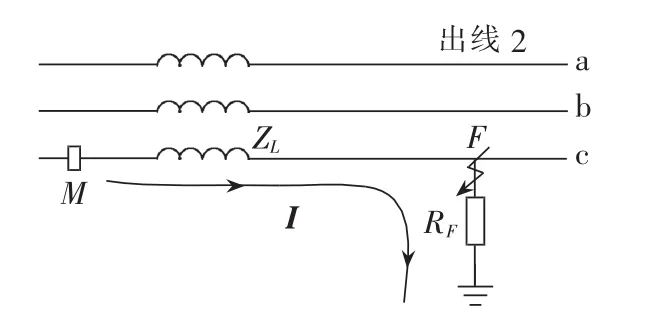
图3 暂态信号故障测距原理图Fig.3 Principle of fault locationbased on transient signal

图3中，M点为变电站出线侧的测量点，F点为故障点，I为频率f下的电流，ZL为线路在频率f下的阻抗，RF为故障电阻。

假定提取暂态信号中频率为f的分量作为待分析量，对于衰减的频率f分量也可利用对称分量法进行分析[18]：

其中，UM、UF分别为M点和F点在频率f下的电压，UM1、UM2、UM0分别为 M 点处频率 f下的正、负、零序电压，UF1、UF2、UF0分别为 F 点处频率 f下的正、负、零序电压，I1、I2、I0分别为频率 f下的正、负、零序电流，ZL1、ZL2、ZL0分别为故障线路在频率 f下的正、负、零序阻抗。

根据各序分量具有独立性可列写下式：

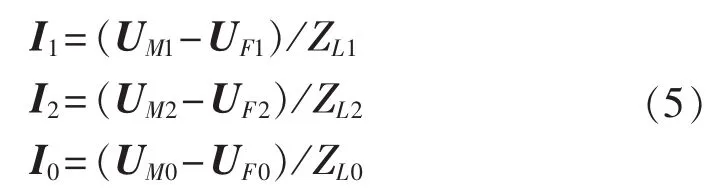
根据单相接地故障边界条件有：

联立式（4）—（6）有：

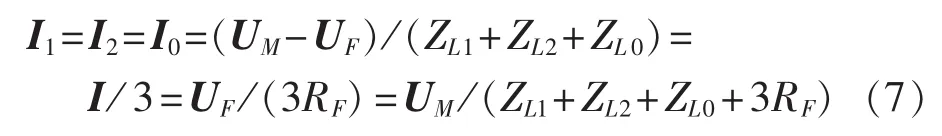
由式（7）可进一步得：

其中，Im 表示求复数虚部；XL1、XL2、XL0分别为故障线路在频率 f下的正、负、零序电抗值；xl1、xl2、xl0分别为在频率f下的线路单位电抗，L1、L2、L0分别为线路正、负、零序单位电感；l为故障线路长度。

由式（8）、（9）可得，利用频率 f下的电压、电流以及线路参数计算出的故障距离为：

将式（10）用幅值和相角形式也可写作：

其中，φ为频率f信号的电压、电流相位差。

可见，若高频分量流经变电站端测量点并经地构成流通回路，可通过对该频率分量定量分析计算出故障距离。在单相接地故障暂态信号中，理论上，充、放电暂态信号均满足条件，但由于充电信号幅值更大，更有利于计算，因此利用充电暂态信号进行故障测距。

3 充电暂态特征提取及故障距离计算

3.1 信号频谱分析和充电频率识别

在提取充电暂态信号特征前，先根据快速傅里叶变换判断充电暂态信号有效性并识别充电暂态信号特征频率。以故障后2个基波周期故障相电压、电流信号进行分析，考虑信号采样频率为10 kHz。

单相接地故障暂态信号集中于 0.3～3 kHz[19]，由于充电暂态信号幅值更大[16]，因此利用该频段内频谱幅值特征确定充电暂态信号特征。首先确定该频段范围内信号幅值极值点，若最大极值点信号幅值大于该频段范围内所有极值点均值的2倍，则判定充电信号有效，且最大极值点信号对应频率为充电信号频率。由于暂态电压信号幅值受线路阻抗、信号频率的影响，不能准确反映信号强弱，因此以电流暂态信号分析为主，以电压暂态分析为辅。

3.2 充电暂态信号特征提取及故障距离计算

确定充电暂态信号频率后，可用时频分析方法提取充电暂态信号并进行定量计算。本文分别用实小波、复小波和S变换法提取充电信号，并进行对比研究，寻找更适合的方法。

3.2.1 实小波变换

小波变换按其变换系数为实数还是复数分为实小波和复小波[20]，经实小波变换提取出的信号仅包含幅值信息。由于充电暂态信号为按指数衰减的正弦信号[17]，因此选择式（12）所示的 Morlet小波为母小波，变换尺度根据母小波中心频率和充电暂态信号频率计算，如式（13）所示。

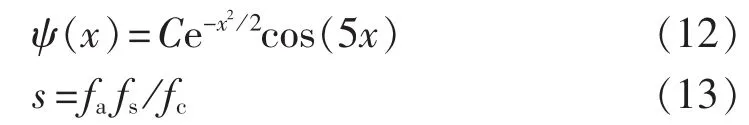
其中，C为常数，s为小波变换尺度，fa为母小波中心频率（可通过MATLAB内置函数计算），fs为信号采样频率，fc为充电信号频率。

图4（a）为实小波变换提取的充电信号幅值，可见其充电信号振荡衰减特性。电压、电流信号的相位差可根据信号对应极值点间的时间差并结合充电频率进行计算，如式（14）所示。

其中，φ为充电频率电压、电流相位差；ωc为充电角频率；fc为充电频率；ts为电压超前电流的时间（即电压、电流对应极值点的时间差），如图4（a）所示。

由于不同故障下暂态信号衰减速度不同，需根据衰减特征确定有效区段，所有参数计算均用该区段内的信号。故障距离用式（11）计算，用电压、电流信号计算对应极值点，计算出的故障距离为一组序列，取有效区段范围故障距离的均值作为最后结果。信号有效区段的自适应确定方法见第4节。

3.2.2 复小波变换

复小波变换实质上是将信号沿2个正交空间分别作实小波变换，系数分别作为变换结果的实部和虚部，其包含信号幅值和相位信息[20]。

同样选择Morlet小波为母小波，图4（b）为复小波变换提取的充电信号幅值曲线图。可见，与实小波变化结果有差异，主要是由于复小波变换结果是幅值相角形式，而实小波变换是瞬时值形式，但其实质基本相同。

由于复小波变换结果为复数值，同时包含了信号幅值和相位信息，故障距离可用式（10）计算。值得注意的是，由于信号衰减，且电压、电流之间存在相位差，因此不能直接用同一时刻值进行计算，需将相位对应转化为时间对应，修正式（10）为式（15）：

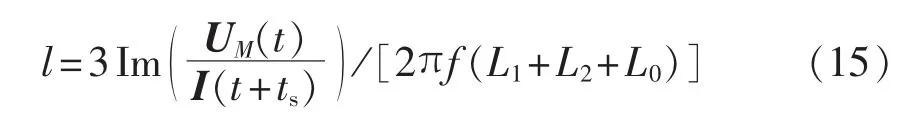
ts可根据电压、电流的相位差并结合式（14）计算，相位差如式（16）所示。

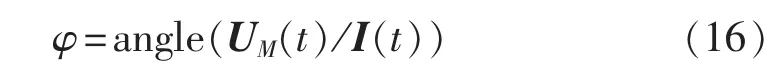
其中，angle（）代表求复数信号相角，UM（t）、I（t）分别为经复小波变换提取出的t时刻的充电电压、电流信号复数值。

与利用实小波变换计算故障距离相似，所有分析均用有效区段范围内的信号进行。计算出的故障距离同样为一组序列，但序列点数大幅增加。

3.2.3 S变换

S变换是以Morlet小波为母小波的连续小波变换的延伸，相当于相位校正后的小波变换，其结果用时频矩阵表达[21]，行为时间，列为频率。经S变换后，由式（17）确定变换结果相邻 2 行的频率差[21]，再结合充电暂态信号频率确定充电暂态信号所在行，提取出该行信号即为充电暂态信号。

其中，Δf为相邻2行的频率差，fs为信号采样频率，N为被分析信号的点数。

经S变换提取出的充电暂态信号与经复小波变换提取的结果相似，均为复数值序列，因此分析处理方法与前面相同。经S变换提取出的充电暂态信号幅值如图4（c）所示，可见经S变换提取的充电暂态信号平滑性更好。

4 自适应确定信号有效区段的故障测距

第1.2节分析了影响暂态衰减特征的主要因素，可见不同故障时暂态信号持续时间差异很大。因此定量计算暂态信号时，若选固定区段信号进行分析，区段选择过长时可能引入无效信号，导致结果准确性和可靠性降低，选择过短则不能保证暂态信号的充分利用，因此需根据暂态衰减特征自适应确定信号有效区段。

原始暂态信号中包含了多种暂态频率分量，而本文以充电暂态信号为分析对象，为避免其他暂态信号对有效区段的影响，确定信号有效区段时利用时频分析提取出的充电暂态信号进行计算。在确定暂态信号有效区段起始点时，由于信号变换法本身的特点，初始部分有一定程度的畸变，如图4所示，可用2个充电信号周期后的信号作有效区段起始点。在确定信号有效区段终止点时，根据信号幅值自适应确定，以充电电流信号为分析对象，对实小波变换提取的信号，以一个充电周期内的信号均方根值RMS（Root Mean Square）小于第1个充电周期内均方根值的5%作为判断标准；对复小波变换和S变换提取的信号，直接以电流信号幅值小于最大幅值的5%作为判据。

图5为经3种方法计算出的故障距离序列曲线图，并给出了幅值自适应确定的信号有效区段。由图可见，经复小波变换确定的有效区段长度为0.0185 s，而经S变换确定的有效区段长度为0.021 s。经S变换计算出的故障距离序列平滑性更好，且其信号有效区段更长，更利于实际应用。

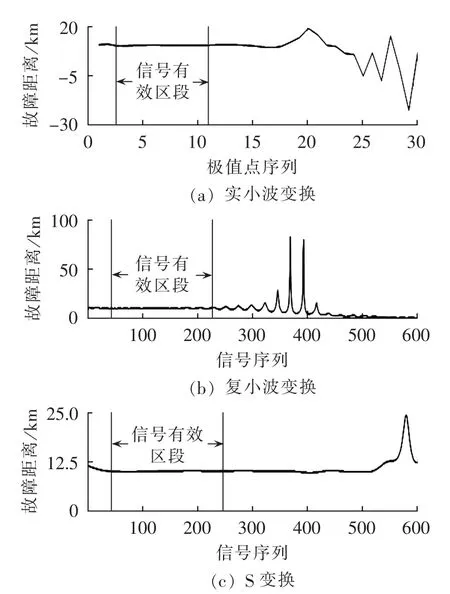
图5 经3种方法计算的故障距离序列曲线Fig.5 Sequence curves of fault distance calculated by three methods

5 仿真验证与讨论

基于MATLAB建立35 kV架空线路模型，见图6。 线路参数如下[12]：正序电阻 0.17 Ω／km，零序电阻 0.23 Ω／km，正序电感 1.2 mH／km，零序电感 5.48 mH／km，正序电容 9.697 nF／km，零序电容 6 nF／km。考虑网络过补偿度为10%，串联电阻值按消弧线圈感抗的10%选取，计算见文献[12]，取电感L=6.92 H，串联电阻R=217.36 Ω。

假设出线1的c相发生单相接地故障，考虑信号采样频率10 kHz。由于充电暂态信号不受消弧线圈影响[1]，限于篇幅，本文仅列出了中性点经消弧线圈接地系统的仿真结果，如表1所示，中性点不接地系统的结果相近，误差计算如下：

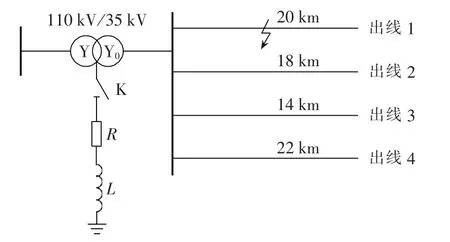
图6 仿真配网结构模型Fig.6 Structure model of distribution system for simulation

为了比较3种方法受故障距离、故障电阻、故障初相角以及噪声的影响，考虑故障距离为10 km，故障电阻为20 Ω、故障初相角为90°、信噪比为80 dB时，比较分析各因素对各方法的影响，如图7所示。

从图7（a）可看出，当故障距离较小时，测距相对误差较大，随故障距离增加，基于实小波变换的方法有一定的波动，而基于复小波变换和S变换的方法则逐渐减小并趋于稳定，故障距离对方法的整体影响不大。图7（b）分析了故障电阻对方法的影响，可见，随故障电阻增大，误差有所增加，主要原因在于故障电阻增大导致信号衰减速度增加，信号有效区段减小，但故障电阻小于70 Ω时，误差小于8%，能满足实际要求。由图7（c）可见，故障初相角对实小波变换影响明显，但对复小波和S变换影响很小。由图7（d）可发现，3种方法的抗噪声能力均较强，仅在信噪比很低时有较小影响。

表1 3种信号变换方法在不同故障情况下的测距比较Tab.1 Comparison of fault location among three signal transformation methods for different fault cases

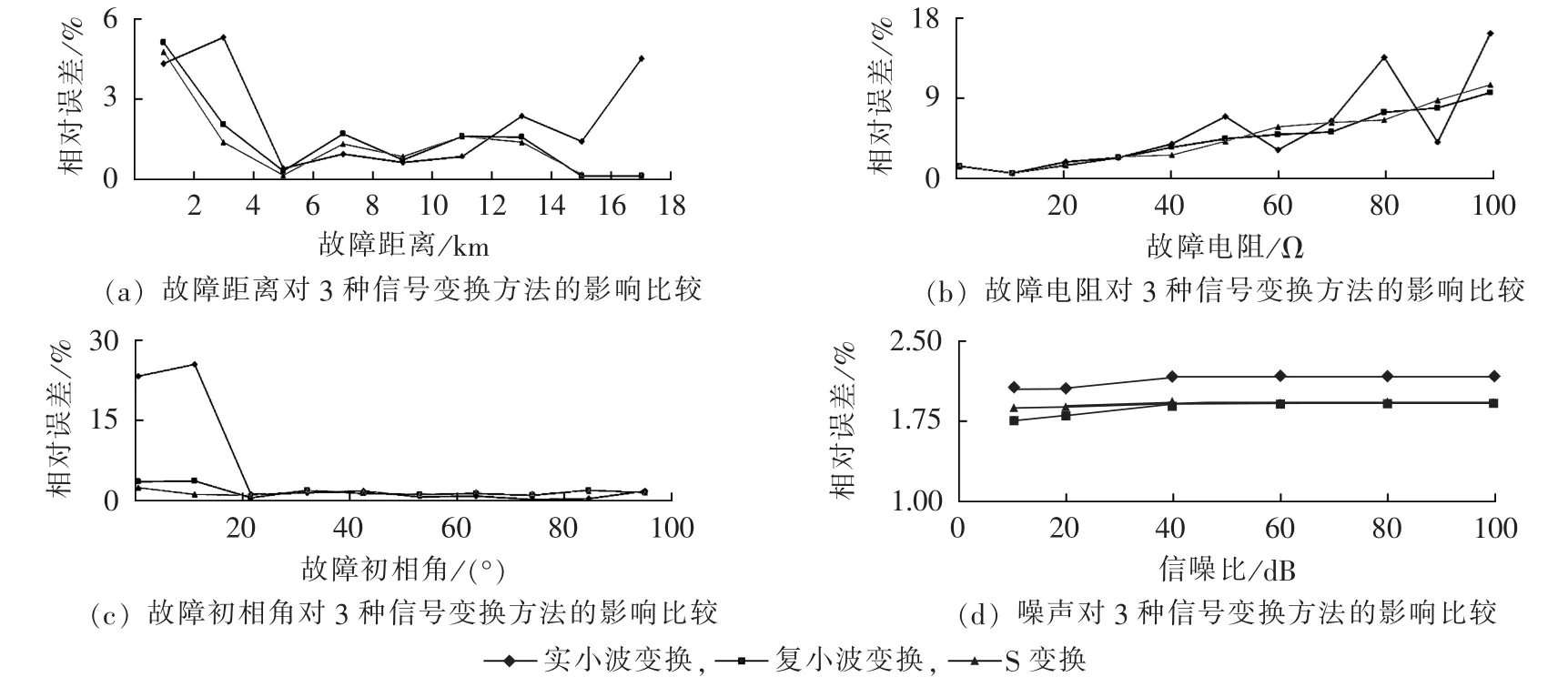
图7 不同因素对3种方法的影响比较Fig.7 Comparison of influencing factors among three methods

结合表1和图7可见，不同故障情况下，复小波和S变换法的测距精度较实小波变换法高，且这2种方法基本不受故障初相角和噪声的影响，受故障距离和故障电阻的影响小，能满足实际测距需要。结合图4和图5，利用S变换提取的信号平滑性更好，计算的故障距离有效序列长度更长，因此S变换法更有利于进行故障测距。

6 结论

根据故障暂态信号及其衰减特征自适应确定信号有效区段，用充电暂态信号定量计算故障距离，保证了暂态信号的充分、合理利用，提高了测距的准确性和可靠性。分别用3种方法提取充电暂态特征，对比研究发现，复小波和S变换法受故障距离、故障初相角以及噪声的影响小，可实现对小电阻接地故障的准确测距。综合考虑变换方法提取信号的平滑性以及信号有效区段长度，S变换更具优势。利用该方法只需进行单端测量，且不受负荷以及系统不平衡影响。

本文对提出方法的原理和实现方法进行了研究，并用仿真证明了方法的准确性和可行性，在工程应用中，尚需对更快速、准确的特征提取方法，以及高阻故障定位和故障分支确定等进行深入研究。