双极性数字限频式电流滞环控制并网逆变器
2013-10-22吴凤江彭浩荣
吴凤江,彭浩荣
(哈尔滨工业大学 电气工程系,黑龙江 哈尔滨 150001)
0 引言
在用于可再生能源发电系统、四象限电机控制系统等的并网逆变器中,为获得清洁高效的并网性能,需要对并网电流的相位和波形同时进行控制[1-4]。
在现有并网电流的控制策略中,电流滞环控制是一种快速电流跟踪的控制方式,具有电流响应快、跟随精度高等优点[5-9]。但电流滞环控制存在开关频率不固定、电路滤波参数设计困难、难以选择最大开关频率容限等问题。随着研究的不断深入,国内外学者提出了一些准固定开关频率的方法。文献[10]通过对滞环电流控制算法的原理和开关频率波动的原因进行分析,提出了基于积分法的定频算法,在保持滞环电流控制算法优点的同时,较好地实现了滞环开关频率的稳定。文献[11]根据逆变器的数学模型,在开关周期固定的前提下,获得电流上升、下降时间随电流电角度的分布关系,进而确定开关器件的导通与关断时刻。但上述方法均采用模拟电路加以实现,过于复杂,实现成本高、难度大。还有一些文献采用数字化方法加以实现[12-16],数字化实现使控制方式更加灵活,但是由于现有高性能算法均比较复杂,对控制芯片的运算资源和采样频率均要求较高,造成实现成本较高。另外,由于数字化实现方法基于离散化采样的控制特点会对控制性能产生影响,造成开关频率仍然存在较大波动。
本文以基于数字化实现的限频式电流滞环控制方法为基础,在采样频率固定的前提下对基于该方法的并网逆变器的控制性能和参数设计准则进行了详尽的理论研究和仿真、实验验证。
1 数字限频式电流滞环控制原理
采用电流滞环控制的单相电压型并网逆变器的原理结构图如图1所示,采用全桥结构。

图1 单相电压型并网逆变器原理结构图Fig.1 Structure of single-phase grid-connected inverter
双极性数字限频式电流滞环控制的基本思想是,取一个固定的采样周期TC,在每一个采样周期,采样实际并网电流i(nTC),计算给定电流i*(nTC),环宽取为零,将二者相比较,比较结果直接作为功率器件的控制信号,比较逻辑为:
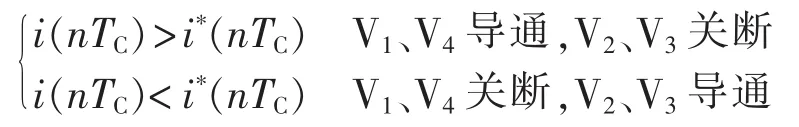
图2给出了基本控制原理。由上述原理可知,该算法以采样周期作为控制信号的最小时基,由此限制了最大开关频率不会超过采样频率的一半。如果根据开关器件的最大工作频率来选取适当的采样频率,就可以使开关器件工作在可控的开关频率。另外,由于在每一个采样点只进行逻辑比较,而不用进行复杂的数学运算,大幅减小了处理器的负担,进而可以和高性能系统控制策略相融合。
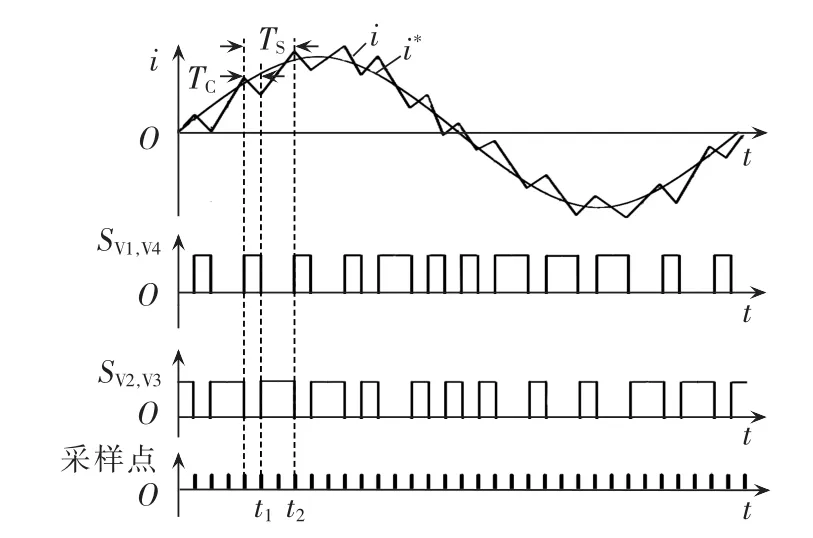
图2 双极性限频式电流滞环控制方法原理图Fig.2 Schematic diagram of dual-polar frequencylimited current hysteresis control
2 性能分析
下面分析开关周期随电流电角度的分布规律、电流纹波表达式及影响其大小的因素。由于并网电流正负半波波形对称,因此只研究正半周的情况,分为 0°~90°和 90°~180°2 个区间分别研究。 假设在一个开关周期中:给定电流为线性变化,电网电压保持不变;给定电流的增量等于实际电流的增量。
2.1 开关周期的分布
2.1.1 并网电流的相角在0°~90°区间
以图1中所示并网电流方向为正方向,有电压方程:

其中,e(t)是电网电压,u(t)是逆变器电压,i(t)是并网电流。由于并网逆变器采用单位功率因数控制,认为 e(t)与 i(t)的相位相差 180°。
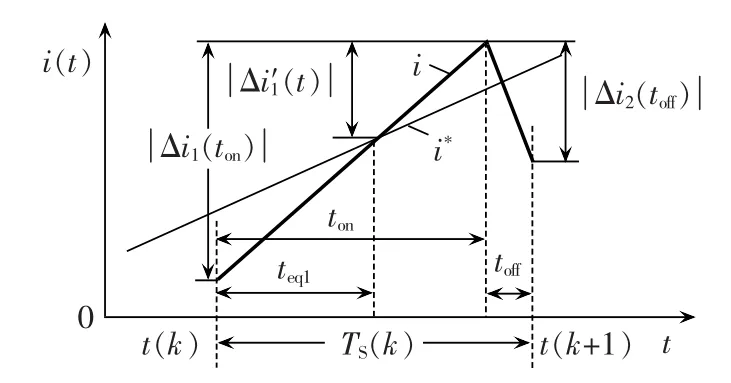
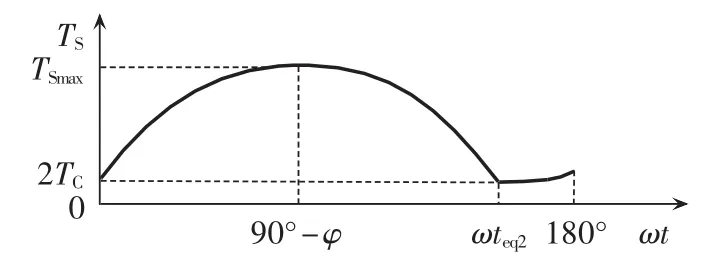
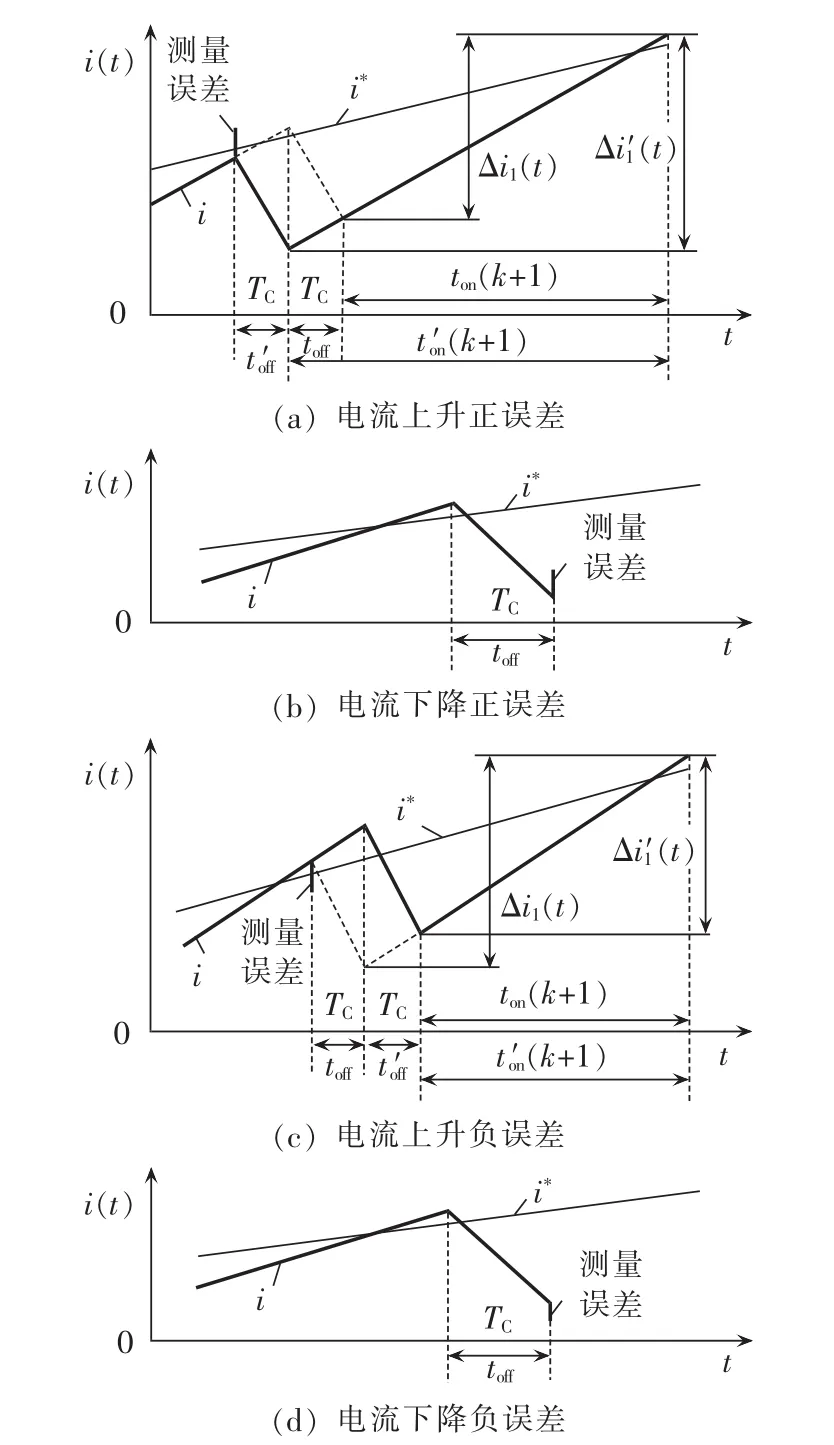
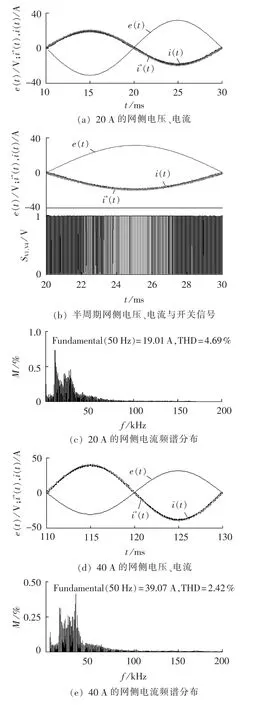
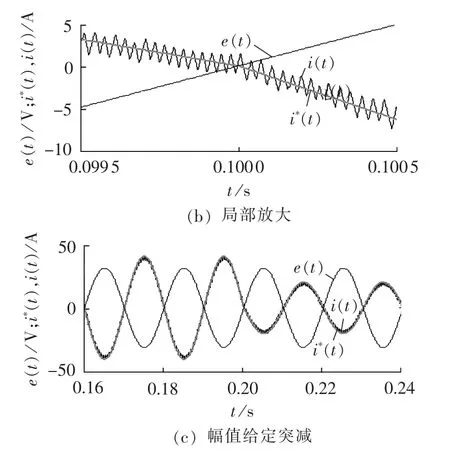
若令并网电流 i(t)=Imsin(ωt)(ω 是电网电压角频率),则电网电压 e(t)=-Emsin(ωt)。 当开关频率远高于电网电压角频率时,第k个开关周期中e(t)可近似为常值,即 e(t)≈e[t(k)]=-Emsin[ωt(k)],其中,t(k)是第 k 个开关周期的起始时刻,t(k)≤t 其中,Udc是直流电压。一个开关周期内-Udc、Udc作用的时间分别是 ton、toff。 在 ton时段,并网电流的变化 Δi1(t)为: 在 toff时段,并网电流的变化 Δi2(t)为: 在并网电流的相角在0°~90°区间时,对于相同的采样周期 TC,由式(3)、(4)得: 下面分析ton、toff与TC的关系,进而获得开关周期的分布情况。一个开关周期的并网电流波形如图3所示。 图3 0°~90°区间一个开关周期并网电流波形示意图Fig.3 Waveform of grid-connected current from 0°to 90° 由算法原理可知,在整个ton时段内,只在t(k)+teq1时刻并网电流与实际电流相等,在此时刻之后,并网电流将进一步上升直到下一个采样点,因此有ton-teq1≤TC。 上式表明,在 t(k)+ton时刻,开关状态发生变化,电流处于下降阶段,在此时刻之后的一个采样周期,必然满足 i(t) 再分析ton与TC的关系。在此区间,有并网电流的斜率大于零,即在任意一个开关周期内,并网电流的增量应大于零,即。 结合式(4),应有 ton>toff。 再由 ton是 TC的倍数,设 ton=nTC(n是 t的函数),则有开关周期 TS(k)为: 下面分析n随时间的分布关系。由并网电流在一个开关周期内的并网电流实际值的增量与给定值的增量近似相等,有: 对于 sin[ωt+(n+1)TC]-sin(ωt)采用线性化近似,给定电流的导数为: 因此,有: 将上式和式(3)、(4)、(7)、(10)代入式(9),并写为t的函数得: 由上式可知,在ωt<90°-φ时,n单调上升;在ωt>90°-φ时,n单调下降。由此得: 则最大开关周期为: 另外根据式(5),在过零点附近有最短开关周期TSmin=2TC。 下面分析最大电流纹波值。由式(4)、(7)可知,最大纹波约等于在峰值附近的值,即有: 2.1.2 并网电流的相角在90°~180°区间 在此区间并网电流最大纹波值与前述分析相同,只需分析开关周期的分布情况。 在此区间,给定电流变化率小于零,则有: 90°~180°区间一个开关周期的并网电流波形如图4所示,存在teq2点,有: 图4 90°~180°区间一个开关周期并网电流波形示意图Fig.4 Waveform of grid-connected current from 90°to 180° 将式(3)、(4)代入式(18)得: 在t 则有: 将上式和式(18)、(19)代入式(17)得: n2为单调下降,在ωt=90°处有最大值: 最小值为 n2min(teq2)=1。 在t>teq2时,有: 则有: 将上式和式(18)、(19)代入式(17)得: 由式(19)得: 则n3为单调上升,最大值为: 2.1.3 总体分布 由此获得双极性调制方式开关周期的分布情况: 其曲线如图5所示。 图5 开关周期分布曲线Fig.5 Distribution curve of switching cycle 以0°~90°区间为例进行分析。 a.在电流上升过程产生正的采样误差,如图6(a)所示。此时将提前进入下降过程,导致在下一个采样点到来时实际下降电流要大于无误差时的下降电流,说明对于下一个上升过程的时间要大于无误差时的情况,但不会对下一个下降过程产生影响,即不会产生累积误差。 b.在电流下降过程产生正的采样误差,如图6(b)所示。由于在一个采样周期内实际电流变化一定会穿越给定电流,因此不会产生影响。 c.在电流上升过程产生负的采样误差,如图6(c)所示。此时将延迟进入下降过程,导致在下一个采样点到来时实际上升电流要大于无误差时的上升电流,说明对于下降过程的时间要大于无误差时的情况,但不会对下一个上升过程产生影响,即不会产生累积误差。 d.在电流下降过程产生负的采样误差,如图6(d)所示。由于在一个采样周期内实际电流变化一定会穿越给定电流,因此不会产生影响。 图6 采样误差示意图Fig.6 Sketch map of sampling error 上述分析说明,在电流上升过程产生采样误差会对其产生影响,但不会产生累积误差,在程序中需要采用过采样等滤波方式来尽量避免上述情况的发生。 本节分析对于事先选取固定的采样频率、为满足谐波要求(小于5%)的参数设计原则。 根据并网逆变器的工作原理,获得电压矢量合成公式: 由于逆变器电压幅值Um≤Udc,则根据上式有: 从电流跟踪瞬态过程看,并网电流过零时的电流变化率最大。为获得最快的动态响应,希望并网电流在一个采样周期内就能够跟随给定电流。因此有: 由此得: 根据前述分析,电感值的大小同样影响最长开关周期。若取最长开关周期为HTC,则有: 推得: 综上所述,为满足综合性能指标,其电感取值范围为: 采用MATLAB/Simulink对基于数字限频式电流滞环控制的并网逆变器进行仿真研究。采用并网电流单闭环结构。电感L=5mH,电网电压幅值为311V,频率为50 Hz;并网电流采样后经过了z变换离散化,以模拟单片机的限频采样,采样频率为40 kHz。 首先分析其稳态性能,电流幅值给定分别为20A和40 A,仿真结果如图7所示。为了对比网侧电压、电流,将电网电压缩小至原来的1/10。稳态时交流侧电流与电压反相。可见,i很好地跟随i*,输出电流波形的谐波畸变率THD=4.69%<5%,满足技术要求。开关信号的开关周期分布与理论分析结果相近。 下面分析其动态性能,在0.1 s时将电流幅值给定由20 A突变为40 A,在0.2 s时突减为20 A。图8是动态仿真结果,并网电流仍然严格跟踪给定电流,获得了较快的动态响应。 搭建了基于30F2010的低成本实物平台,进行实验研究,实验参数与仿真模型相同。实验结果如图9所示,Sc是采样信号。由图可知,并网电流具有较好的正弦性,与电网电压反相,功率因数接近于1。开关信号频率在最大时约为采样信号频率的一半,验证了所采用的限频式滞环控制方式的正确性。在动态变化过程中,并网电流相位始终严格跟随电网电压。 图7 稳态仿真波形Fig.7 Steady-state simulative waveforms 图8 动态仿真波形Fig.8 Dynamic simulative waveforms 图9 实验波形Fig.9 Experimental waveforms 本文获得了采用数字限频式电流滞环控制算法的并网逆变器在采样周期不变、无滞环宽度情况下的开关周期随电角度分布的量化表达,从机理上揭示了该方法的性能特点,并进一步给出了相应的参数设计原则。相应的理论分析和仿真、实验结果表明,该方法通过固定采样周期,限制了最大开关频率,通过合理选择滤波器参数,获得了满足并网要求的控制性能,进而为其实用化以及进一步性能优化奠定了基础。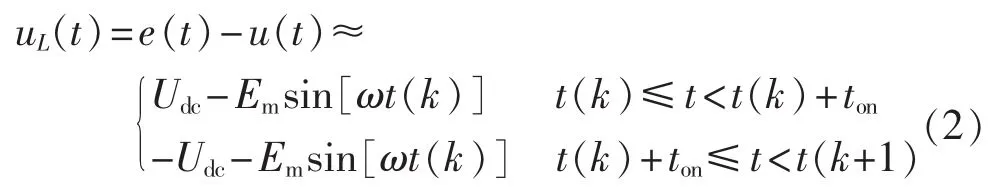
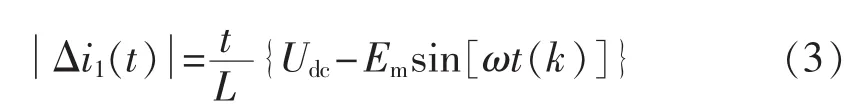

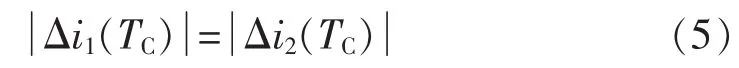


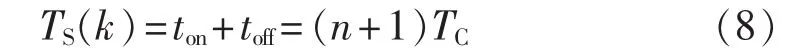

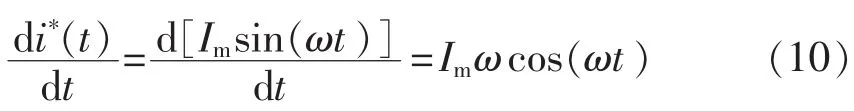
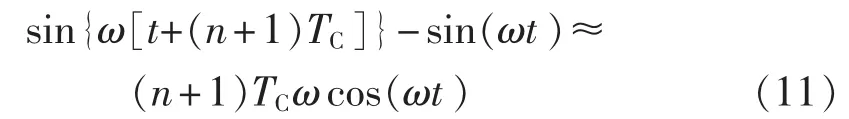

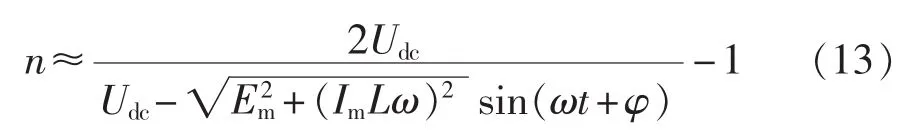


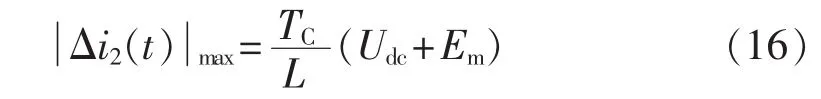
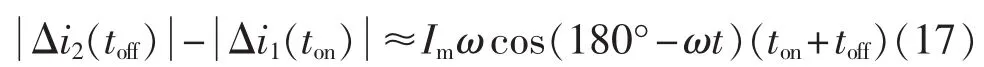



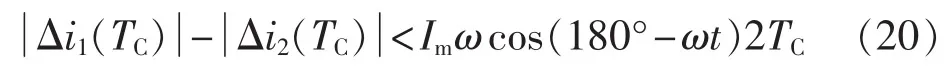

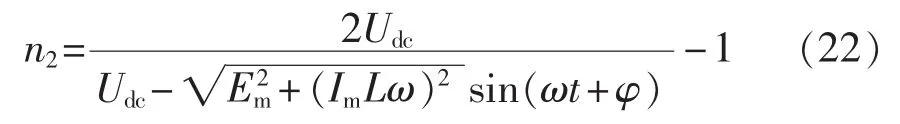



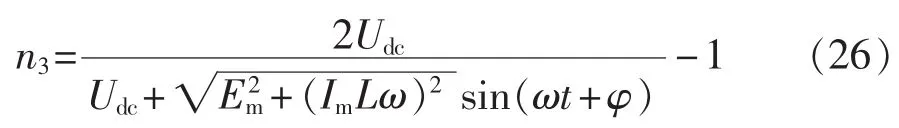



2.2 采样误差对开关频率的影响分析
3 滤波器参数设计
3.1 满足并网逆变器电压限制时的电感设计


3.2 满足电流快速跟踪能力时的电感设计

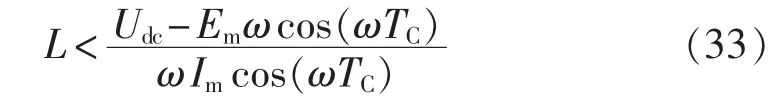
3.3 满足电流谐波要求时的电感设计

3.4 最长开关周期的限制
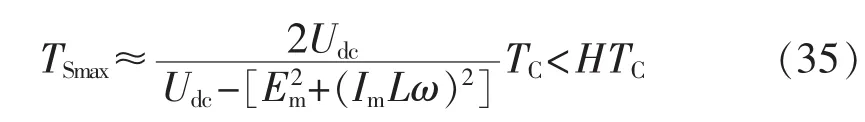
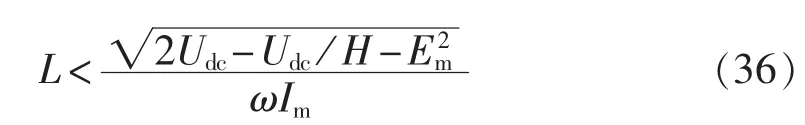

4 仿真与实验结果及分析


5 结论
