避免电网连锁解列的全局协调控制策略

胥威汀，刘俊勇，李 旻，丁理杰

（1.四川大学 电气信息学院，四川 成都 610065；2.四川省智能电网重点实验室，四川 成都 610065；3.四川省电力试验研究院，四川 成都 610072）

0 引言

大型跨区输电系统能够有效缓解区域资源供需不平衡问题，但随着其规模的增大，连锁故障的危害不容忽视[1]。 连锁故障后期[2]，局部的汽门调节、励磁调节或切机切负荷等控制措施均会失效，此时应立即以打破网络结构为代价来隔离故障，执行解列操作。作为大规模电网安全保障体系的最后一道防线[3]，解列控制要求能够可靠地终止或缓解故障蔓延，并且在非常规运行状况下，尽可能多地保留系统对负荷的电力供应[4]。

工程应用中，参与解列操作的元件主要为失步解列装置。由于高可靠性要求，其动作整定值基本不考虑系统全局情况，而仅基于局部电气量，如视在阻抗、ucos φ、阻抗角等[5]。 所以装置的动作时机完全依赖于扰动的传播情况。然而，由于多个装置间存在电气位置上的差异，识别到系统振荡中心或动作判据的时刻不同，这就产生了时间尺度上的连锁跳闸现象。这样的无序跳闸对系统造成的连续冲击会带来更多的不确定性影响，导致达不到解列控制的效果[6]。避免连锁解列现象需要从两方面入手：确定解列面，防止不必开断的线路自行参与解列；确定解列时机和开断顺序，避免无序动作。这2点分别属于主动解列研究领域的Where问题和How问题[7]。下面就这两方面的传统方法和研究文献作简要概述。

目前国内外文献中，针对Where问题的理论研究比较丰富，主要沿用2种思路：基于扰动后的发电机同调识别结果，进行功率平衡等约束下的割集搜索[8-10]。该思路主要面临的问题是对多项式复杂程度的非确定性多项式NP（Non-deterministic Polynomial）完全问题的实时求解，所以更多的创新点在于对解空间的缩减，例如 Krylov 映射[8]、基于图论的化简[9]以及基于电气距离的网络划分[10]等；受扰前对电网进行预分区，需要解列时按照发电机同调情况选择把某些预分区与剩余部分解开[11-14]。由于预分区没有考虑故障信息，在操作有效性上不如第1种思路，但该类方法把大部分NP完全问题的求解过程都放在离线或在线阶段，所以在处理大规模电网时有速度上的优势。典型的预分区方法包括慢同调[11-12]、潮流追踪[13]、节点电压相角同调性[14]等。 该思路的主要难点在于如何保证受扰后系统的内在规律仍在预分区的范畴之内，以确保执行解列方案后系统能够满足动态稳定和静态功率平衡等约束。慢同调分区是一种非常有效的预分区手段，文献[11]充分地验证了该线性化分析方法在大扰动环境下的良好表现，该文献的不足之处在于对非发电机节点也进行了预分区，这难免会因为故障的影响导致预分区失效，如故障直接导致部分预分区功率不再平衡等。总而言之，第1种思路的矛盾在于NP完全问题的处理效率和网络化简程度带来的有效解损失，而第2种思路的矛盾在于预分区的细化范围和故障扰动对预分区的否定程度。如果能够结合预分区方法的优势，并对NP完全问题进行有效转化，可以找到兼顾2个矛盾的突破口。

对于How问题的理论研究比较少见。目前还没有针对有序解列的研究，但文献[15]给出了一种“激活-闭锁”策略，能够适当引导解列的发展：按照系统主导两机失稳模式确定解列面，闭锁非解列面的解列装置，同时激活解列面上的解列装置，让这些被激活的装置自行可靠检测判据并动作，如此依次完成两两机群解列。为了避免解列面上的连锁跳闸现象，文献[6，16]认为一旦确定了解列面和解列必要性，应立即主动控制相应装置一并速动。2种思路分别着重于判据的可靠检测和连锁跳闸现象的规避，各有利弊。

在现有相关研究基础上，本文选择结合预分区、NP完全问题转化、可靠识别动作判据和解列面速动的思路，提出一种解列分析策略。该策略能够快速确定有效解列面，捕捉解列时机，避免连锁解列。运用到的工具主要包括慢同调理论、平均数充分性MIA（Mean Index Adequacy）同调群识别法、基于图论的网络化简和改进的K-Medoids聚类。下面的章节主要介绍解列分析流程及工具基本原理。仿真算例验证了该解列分析策略的有效性。

1 解列方案的决策流程

考虑到孤岛运行中发电机功角稳定的重要性和预分区的优势，首先需要在线对系统机组进行慢同调分区。虽然扰动不会对慢同调分析结果造成显著影响[11]，但很可能会影响到网络连通性和功率分布等，所以该阶段不对非发电机节点进行分区。这也即是对Where问题2种思路的折中。

系统发生故障后，不一定每一个慢同调机群都会相对其他机群发生失步，所以并非每一个预分区都需要执行解列；另外，如果扰动引发的是局部振荡而不是大范围的区间振荡，也没有必要执行解列。是否需要解列以及怎样划分机群，需要进行发电机同调性识别。现有方法主要包括Prony识别[15]、同调度识别[8]、流形变换[17]和 PMU 直接测量等。 其中流形变换存在难以求取实际系统中主导不稳定平衡点CUEP（Controlling Unstable Equilibrium Point）不稳定流形的问题，而其余3种方法本质上都是直接基于各发电机状态量之间角度差的判别方法，阈值设定的有效性是共同的难题。本文在该阶段提出一种基于慢同调分析的机群同调性识别方法——MIA识别法。该算法能够利用慢同调分析结果提高同调识别的分析效率。

机群划分方案确定之后，需要实时确定解列割集，但解列割集只能在边界网络中搜索[11]，所以首先需要快速提取边界网络。采用的方法是基于有权无向图[9]的广度优先搜索 BFS（Breadth First Search）树形搜索[12]。保留边界网络，把各同调机群覆盖的网络聚合为一个正功率节点，就能形成简化的系统拓扑图，极大缩减割集搜索范围。

由于预分区阶段并没有将分区方案细化到非发电机节点，所以前面的步骤保留了传统的实时NP完全问题，即孤岛功率平衡约束下的解列割集搜索。当前应用于NP完全问题的解列决策方法包括蛮力搜索[11]、改进的 BFS[8]和有序二叉决策图 OBDD（Ordered Binary Decision Diagrams）[9]，然而它们始终存在受限于网络规模的问题。对NP完全问题的有效转化是最为关键的突破口。数据挖掘技术在处理海量、高维数据方面具有显著的优势，考虑到电力系统孤岛运行带有明显的区域分布特点，倘若能把搜索可行解列面的问题转化为一种聚类操作，便能有效地避开对每一条线路进行考核的搜索模式，极大提高决策速度。按照该思路，在前面步骤的基础上，提出一种改进的K-Medoids聚类法，以控制形成满足功率平衡约束的孤岛。

为了避免由于扰动的传播造成的连锁解列现象，解列方案确定后，应立即闭锁非解列面上的解列装置，并激活解列面上的解列装置。但为了可靠动作，仍然应该让解列装置检测到区间失步信号后才实施跳闸[15]。所以只要任一被激活的失步解列装置检测到动作判据，全局目标线路集上的解列装置即同步速动，执行解列操作。

本文提出的解列方案决策流程图如图1所示。

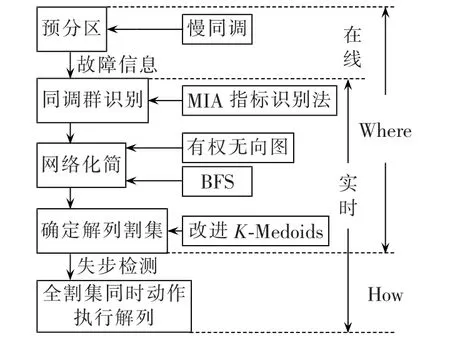
图1 解列方案流程图Fig.1 Flowchart of split scheme

2 算法原理及其可行性讨论

2.1 多机系统慢同调预分区

发电机慢同调是一种多机系统的聚合标准。发电机同调性对应着系统的某些动态模式，而慢同调性即对应着其中的慢机电模式。如扰动发生后，电气连接非常紧凑的发电机将同步摇摆，它们被称为同调群，它们之间存在相近的动态模式，所以扰动在其内部的传播速度非常快；相反，同调群之间的弱连接即对应着慢机电模式，它们抑制了扰动的传播，如果在扰动传播到下一个同调群之前切断这些弱连接，扰动将被有效控制在一个机群中。因此，该理论常用于系统的动态化简。这样的特征分析能很好地适应于非线性干扰，即机间同调性对扰动信息不敏感，是系统的固有特性。由于慢同调是比较成熟的理论，这里不再赘述，数学表达详见文献[11，18]。

2.2 基于慢同调的MIA同调群识别法

MIA指标是一种用于确定最佳聚类数的测试型指标[19]，在样本规模M不大时，分析速度非常快。由于慢同调分析往往只形成很少的分区，例如采用DYNRED软件对30000节点、5000机组成的北美东部互联系统进行慢同调分区也仅形成了18个慢同调机群[20]，所以在大型电网中运用基于慢同调分析的MIA指标进行同调性判断是可行的。

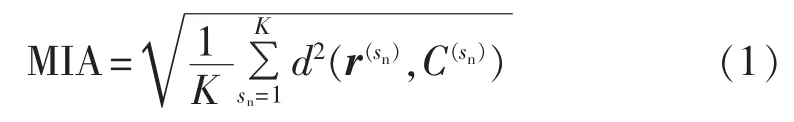
其中，类别编号 sn=1，2，…，K，K代表类别总数；d（r，C）表示样本子集C中所有样本到该子集中心r的距离之和，本文中，样本为各慢同调分区惯性中心的相对功角值及其对时间的微分[δ，dδ／dt]，r可由常规K-Medoids算法获取。该指标值越大，说明各子集的聚集性越差，即K个类别的划分方法对于该样本越粗糙，相反越精细。当然，MIA并不是越小越好，因为该指标通常与分类数呈单调递减关系，所以MIA减小伴随的是聚类数的增大，聚类操作逐渐失去意义。

对于确定解列后的孤岛数而言，当然更不能让K值没有控制地增大，比较合理的方法是关注K对应的SK值，如式（2）所示。若SK大于某个阈值ε，说明该样本分为K类明显优于分为K-1类，视为有效分群数。应按K值从大到小测算SK，选择第1个满足要求的K值作为最佳机群分组数Kp。例如，图2中S7为第1个有效分群数，那么Kp=7。可以明显看出，图中K>7对应的MIA变化已经不明显。

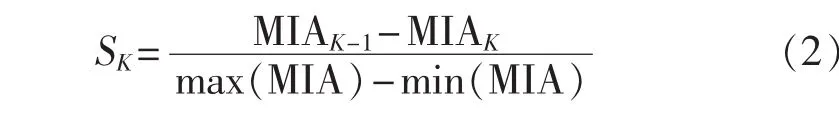
图2 某一时刻的MIA曲线示意图Fig.2 Schematic diagram of MIA for a moment

若随着时间的推移Kp取值不稳定，说明当前系统中的发电机还没有出现显著的分群模式，应随PMU采样即时更新MIA，直到获取稳定的Kp值。若Kp不变且保持有效，达到延时tp后，进入下一阶段。

为了排除区内失步导致对MIA的误判，在确定Kp后需要验证系统的主导失步模式是否为区间失步。首先通过2种方式把所有n个发电机分为Kp类：方式Ⅰ按δ的分类情况把各发电机归类；方式Ⅱ按照各发电机功角δgi进行聚类。由于区内失步会使其所属慢同调群的δgi聚集性明显变差，所以考察每一个慢同调群内，所有发电机分别到方式Ⅰ隶属聚类中心r1和方式Ⅱ隶属聚类中心r2的距离最大值和最小值之差 DK（r1，δg）、DK（r2，δg），如式（3）所示，其中δg=[δg1，…，δgn]，r代表 δg中各元素对应的聚类中心序列。定性地认为：如果发生的是区内失步，某个慢同调分区内将出现明显的功角轨迹分离，聚类中心的分布将大幅转移，DK（r1，δg）相对于 DK（r2，δg）会相当明显，区间失步则相反。所以可以进行如下判断：如果 DK（r1，δg）>λDK（r2，δg）（λ 为判定系数），说明发生的是区内失步，否则Kp值可靠输出。

对于比较特殊的情况：极端故障导致某个断面开断，分割某慢同调机群，应直接按照这样的划分方式把该慢同调分为2个慢同调群，相应在MIA同调识别过程中增加一条惯性中心曲线即可。由于受扰前后，慢同调群之间都由弱连接相连，仍保持慢同调关系[11]，所以其他慢同调群的构成不变。

2.3 基于发电机同调群识别的边界网络界定方法

提取边界网络，首先需要把系统转化为带权无向图[9]G=｛V，E｝，其中 V=｛V1，V2，…，Vm｝代表 m 个系统节点的顶点，E=｛ei-j｝是对应电力线路的边集。同时，构建2种网络数据结构：顶点结构，顶点号、顶点类型（发电机或负荷）、所属同调区编号（非发电机节点对应初始值为0）、电压等级、有功功率、无功功率；链接结构，与当前顶点连通的顶点号，这些顶点号对应的节点也通过该数据结构与当前顶点相连。以上数据结构包含了系统的拓扑和解列分析需要的信息，均可通过矩阵形式储存并操作。

边界网络的界定步骤如下。

a.输入数据：顶点结构、链接结构。

b.确定边界机：从任意同调群内发电机出发进行BFS，找到的第1个异名同调群发电机，设定为边界机。

c.搜索边界网络：从该边界机出发，进行BFS（所有属于任意同调群的机组都设定为路径终点），得到粗糙的边界网络。

d.修剪边界网络：对每一个同调机群进行基于BFS的连通性检验，修复被边界网络隔断的路径。

e.孤立该边界网络，返回步骤b。

该步骤的输出为一系列边界网络Nb和Kp个包含同调机群的网络Nc。解列方案分析只需在Nb中寻找能有效解开Kp个Nc的线路集合即可。

由于Nc内部的边不参与解列，并且该阶段仅考虑系统的静态功率平衡问题，所以可以分别把各Nc中的顶点按照功率累加的方式聚合成一个虚拟顶点。该项简易的操作能够为后面的分析屏蔽掉大量不参与解列的线路，缩减了网络规模。

2.4 孤岛功率平衡约束下的解列面聚类决策法

最终方案决策用到的算法为K-Medoids聚类，该算法为K-Means算法的衍生，对坏数据不敏感。常规的K-Medoids需要计算样本间的欧氏距离，并以此作为聚类判据的基础。但对于电力网络而言，由于存在具体的线路连接，所以节点间的关系无法直接表达为欧氏空间中的距离（如地理位置关系等），因而也不便于设定顶点在欧氏空间中的相对位置。算法需要改进，主要从顶点间的距离表达方式入手。

定义一个对应网络拓扑的权重集合W=｛wij｝，把wij分配给连接顶点Vi和顶点Vj的边，初值取1。利用边集E和权集W建立一个用于表达该网络结构的邻接权矩阵 A=[aij]，式（4）为 aij的确定方法[21]。

利用A可以计算任意顶点间的最短路径的权重值，并以此作为两顶点间的距离，方法如下：对于Vu到 Vv间任意路径 p=｛Vu，…，Vv｝，权重 w（p）等于该路径所经过的边的权重之和，那么可以利用式（5）表示 Vu到 Vv间的距离 β（Vu，Vv）。

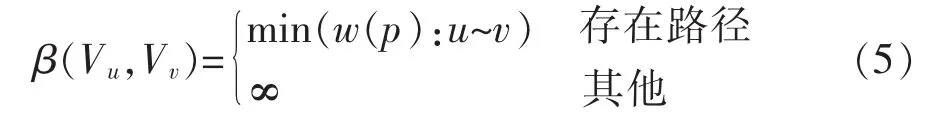
构建距离矩阵 B= [βij]，其中 βij=β（Vi，Vj）。 对于实施解列前不存在孤岛的系统而言，初始B中不会出现∞元素。矩阵B即改进的K-Medoids算法的输入量。为了尽可能地满足孤岛功率平衡约束，需要在执行聚类分析之前对B进行调整。

调整原则为：缩减发电机顶点VG和附近的能够平衡VG功率的负荷顶点VL之间的距离，增大必须归入不同孤岛的VG间的距离。具体步骤如下。

a.把所有由Nc聚合而成的虚拟顶点设定为VG，所有Nb中的顶点设定为VL，顶点处消耗的功率统一设定为负值，发出的功率设定为正值。

b.识别 VG，重新定义 VG间的距离 β（VGi，VGj）=max（β（VGi，VGj））+1。

c.选定一个VG，把所有VL到该VG的距离按照从小到大的方式排序，存入列向量lp。

d.构建一个列向量lpsum，其第n行元素为lp中1～n行元素的有功功率累加值。

e.用lpsum的每一行元素减去当前VG的有功功率值，把结果存入列向量lpbal。向量lpbal中为负值的行，对应着lp中能够得到当前VG功率支撑的VL，它们到当前VG的距离应该被缩减。

f.把需要缩减的 β（VG，VL）对应的路径上的各边权 w 乘上系数 R，Rє（0，1）。 返回步骤 c。

g.更新B。

改进的K-Medoids算法的输入量为更新后的矩阵B，聚类数取同调群数Kp，初始聚类中心μ取系统中的所有VG，收敛判据为第i次迭代与第i-1次迭代的μ相同（聚类中心不再变化）。利用B进行KMedoids分析不需要再计算各样本间的距离，只需要在B中查找对应的距离信息，把每一个顶点归入距离最近的μ，并按照式（6）更新聚类中心，直到收敛。

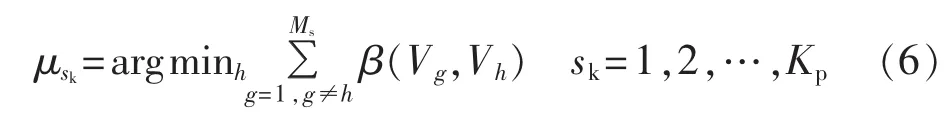
其中，g和 h为第 sk类中顶点的编号，取值为[1，Ms]内的整数，Ms为该类中顶点的数量。

对于每一次迭代中可能出现的临界点（与不同μ等距的V），在完成所有非临界点判别之后再考虑其归属。按照以下原则进行判别：

a.临界V的判别不能让自身或邻近V被孤立；

b.在此基础上，如果临界V的有功值为正，将其归入有功缺额较大一方，否则归入有功缺额较小一方。

由于该算法直接以边权w作为顶点间的距离表达形式和距离调整渠道，所以保证了各顶点不会跨越异名顶点找到其隶属的μ，即算法输出的解列面为有效割集。输出信息包括孤岛拓扑结构和参与解列操作的线路集合，即最终解列方案。

3 算例

3.1 仿真过程和结果

仿真采用IEEE 118节点网络，程序实现基于MATLAB7.6.0平台。发生故障前拓扑结构如图3所示。实心顶点代表发电机节点，空心顶点代表负荷节点。发电机采用经典模型[22]。根据慢同调理论，发电机被划分为3个慢同调群，如表1所示，表中第3列为各发电机群惯性中心编号。

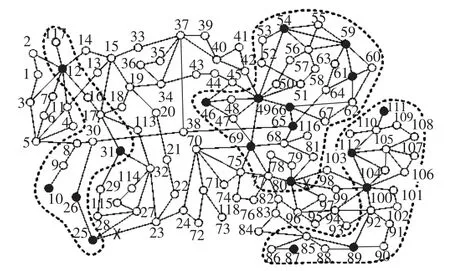
图3 IEEE 118节点网络结构及其同调群示意图Fig.3 Structure and coherency groups of IEEE 118-bus network

表1 发电机慢同调分群结果Tab.1 Result of slow coherency generator grouping

0 s时刻e23-25对应的线路在近节点25处发生三相短路，0.07 s时刻e80-99对应的线路在近节点80处发生三相短路，2处故障分别于0.17 s和0.21 s切除。扰动后19条功角曲线和3条慢同调群惯性中心曲线如图4、图5所示。如果不执行协调解列控制，部分联络线上的解列装置（R-Rdot[15]）将于 1.0 s 左右开始，先后检测到动作判据，连锁跳闸，时间跨度达数秒。

图4 扰动后的发电机功角变化曲线Fig.4 Curves of generator power angle change after disturbance

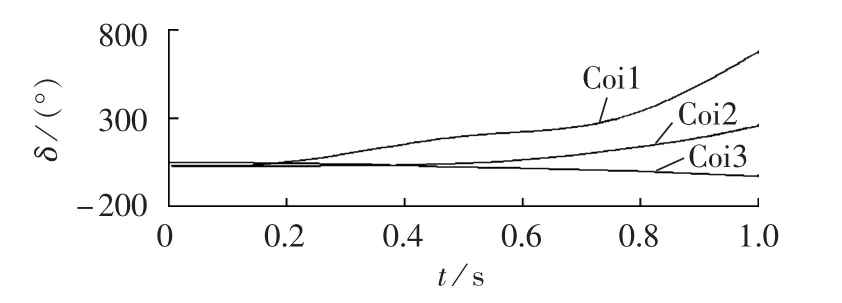
图5 扰动后的慢同调群惯性中心曲线Fig.5 Inertia center curve of slow coherency groups after disturbance

故障发生后应该首先进行同调机群识别。实时采集19台发电机的瞬时功角，并以此计算3个慢同调群的惯性中心，以相应 3 组[δ，dδ／dt]作为当前时刻的MIA指标分析输入量。设阈值ε=0.1，tp=0.2 s，λ=2.0，以0.02s为周期更新Kp，同步曲线如图6所示。

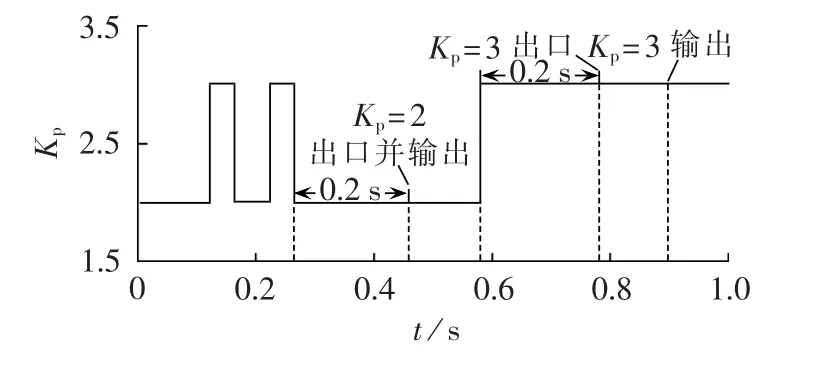
图6 MIA实时分析模块中Kp的状态变化Fig.6 State change of Kpin module of real-time MIA analysis

可见，数值仿真过程中，第1个有效tp后（0.46 s）得到出口Kp=2，并且验证为区间振荡（见表2中相应D1I和D1II），Kp=2可靠输出，生成解列方案，相应解列装置准备动作。但由于扰动传播延时，一段时间内还未有激活的装置检测到动作信号，所以尚未执行解列方案，继续监测功角变化。0.58 s时刻Kp状态由 2 变为 3，保持 0.2 s（tp）后，于 0.78 s得到出口Kp=3，即刻撤销原解列方案。0.89 s时刻3个慢同调区域均检测到区间振荡判据，立即以Kp=3对应的分类方案划分发电机，并向后续步骤输出该结果。下面以3群解列为例展示后续分析。

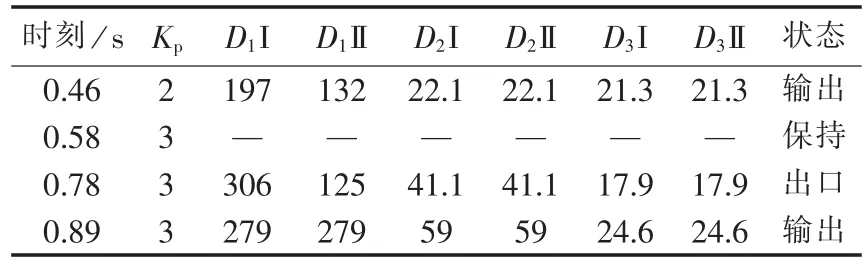
表2 同调识别模块的出口验证Tab.2 Outlet certification of coherency identification module

发电机分群方案确定之后，应界定解列面的搜索范围，即找出系统的Nb。随机取节点10为根节点进行BFS，得到第1、2机群间的Nb中的一台边界机节点65，并以此为根节点进行BFS获取粗糙Nb。同理，可以得到系统所有粗糙Nb。对粗糙Nb完成修剪后，界定出3个Nc，如图3中虚线所示。所有Nc聚合为虚拟节点后的系统结构如图7所示。为便于后续分析，本算例中把各虚拟节点命名为相应Nc内某发电机节点的编号，以保持顶点结构和链接结构的完整性。

图7 边界网络Fig.7 Boundary network

下面基于图7的边界网络进行改进的K-Medoids分析。 首先利用式（4）、（5）得到矩阵B，再按照功率平衡要求调整B，调整方法示例见表3，表中序号指按与V10距离由近到远对系统顶点排序的序号。以 V10为例，前 28 个 VL的 lpbal（VL）值为正，说明输出功率为902 MW的V10能够为这些VL提供有效电力支撑，应在B中减小相应的β值。例如，β中路径 p（V22，V10）= ｛V10，V32，V23，V22｝需要缩减，那么调整 w（V10，V32）=R w（V10，V32），并对 w（V32，V23）和w（V23，V22）进行相同处理，三者累加即可得到缩减后的 β（V22，V10），该算例中调整系数 R 取 0.7。

表3 以V10为例选取距离调整对象的步骤Tab.3 Steps of object selection for distance regulation of V10

以3个VG作为初始μ进行改进的K-Medoids分析，迭代2次后得到最终解列方案，见图8。Nc1和Nc2解列面上的所有线路于1.53 s时刻同步速动（由e23-24检测到动作判据），Nc2和Nc3解列面上的所有线路于1.16 s时刻同步速动（由e80-98检测到动作判据）。若不计网损、不切负荷，解列后的3个孤岛的静态功率平衡分别为：+63 MW、+21.4 MW和+51 MW。当然，解列操作往往伴随着恶劣的系统运行环境，若要保证孤岛内的稳定运行，切机切负荷操作不可避免。作为后续研究，切机切负荷策略不在本文讨论范围之内。

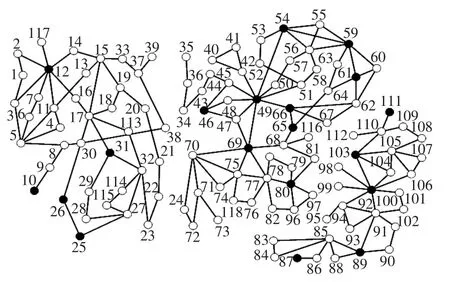
图8 改进K-Medoids分析得到的解列方案Fig.8 Split scheme obtained by improved K-Medoids analysis

3.2 解列策略的实效性分析

本算例实时运算总耗时约为0.076 s，其中Kp计算耗时不足0.01 s，解列面分析耗时约0.01 s，Nb界定耗时约0.062 s。因为要求全程（从故障始发到解列面的装置完成动作）保持发电机功角监视和MIA测算，所以该方法可以根据具体情况灵活校正解列方案，运算速度完全能够达到要求。

值得注意的是，改进的K-Medoids方法中最耗时的步骤是矩阵B的构建和更新，其本质为NP完全问题中的“二元遍历”的转化，长约4 s，所以不可能实时完成。处理方法是：在线定期更新并寄存所有顶点间的路径（边集），在实时分析阶段通过查找的方式把故障信息及距离更新信息接入矩阵B即可。这使得该方法的实时运算速度大幅提升。

若按照文献[11]中提到的方法，在图7的基础上使用蛮力搜索寻找一个可行解列割集，取不同的初值，平均耗时长约10 s。以其中一个方案为例，计算耗时14.74 s。3个分区的静态功率平衡情况为：+65 MW、+1.4 MW和+69 MW，第2个孤岛可容纳网损的空间太小，可能造成严重的频率偏移。可见，传统方法的计算效率和功率分配情况都不如本文提出的搜索策略。

4 关于各种系数阈值设定的讨论

MIA同调群识别法中，阈值ε的设定非常关键，直接关系到Kp取值。传统研究中，由于样本的随机性和复杂性，基本通过人工观察MIA指标曲线来离线获取Kp[19]，所以不存在阈值设定的问题。但在同调机群识别中，样本有一定规律：大型跨区电网中通常有明显的弱连接，扰动导致机间振荡时往往会有明显的同调曲线簇，这保证了MIA值会在某一个K值上显著减小。所以，阈值ε可以设置得相对较大，这也能在一定程度上避免形成孤岛数过多的解列方案。当然，ε的设定需要根据网络规模、慢同调特性和试验仿真结果而定。但其值不必非常精确，因为本文用到的MIA分析基于慢同调结果，本身具有一定的容差能力。

延时tp是一个比较自由的指标。因为实时运算的速度很快，所以可以把tp设置得相对较小，以方案调整频次为代价尽早形成可行解列方案。

由于局部失稳和区间失步的功角曲线差异非常明显，所以出口判定系数λ可以设置得较大。

改进的K-Medoids算法中，调整系数R对结果影响很小。由于顶点间的初始距离以线路数（整数）表示，所以只要R<1.0，就能起到距离调整的效果。

需要额外说明的是，当慢同调分区数M=1时系统不适合实施解列控制，M=2时更多的分析应集中于解列可行性问题。本文提出的MIA同调群识别法适用范围为M≥3。

5 结语

本文提出了一种应用于解列操作的全局协调控制策略。该策略主要运用慢同调分析、MIA同调群识别法和改进的K-Medoids聚类分析得到满足发电机同调性和静态功率平衡要求的解列面，并通过持续的MIA指标监测和解列面同步速动的策略避免了发生区间失步时伴随的连锁解列现象。该方法具有功能结构明确、计算速度快的优点。仿真算例验证了其可行性和实效性。

没有考虑即将形成的孤岛中电气设备的静态载荷能力和无功电压支撑是该方法的不足之处，将在后续研究中力求解决。该方法仅作为一种新的参考思路予以提出。