基于改进最小方差法的风电机组变桨距控制

赵亮，赵大伟，张磊，钱敏慧，陈宁，朱凌志

（中国电力科学研究院，江苏南京 210003）

当风速超过机组额定风速时，由于机组机械强度和发电机、电力电子容量的限制，风力发电机组的风轮必须降低能量捕获，使输出功率保持在额定功率值附近，同时限制叶片载荷和整个风力机受到的冲击，保证风力机安全运行。因此，在额定风速以上，风力发电机组的控制目标是限制能量捕获，保持额定功率输出。变桨距控制是最常用的限制风力机吸收风能的方法，在高风速时通过调整桨叶节距角，从而改变风力发电机组获得的空气动力转矩，使功率输出保持稳定。随着并网型风力发电机组容量的增大，大型风力机叶片己重达数吨，操纵如此巨大的惯性体，并且保证较快的响应速度相当困难，所以变桨距控制技术是大型风电机组控制技术研究的重点之一。

由于风速的随机性和不确定性，塔影、风切变、偏航回转等引起的负载扰动，变桨距开关桨的往复动作，液压或电机驱动大质量叶轮负载的惯性环节，使得变桨距控制系统有参数非线性、参数时变性、大惯性等技术特点[1]，常规的PID等控制方法难以达到良好的控制效果。文献[1-4]采用神经网络等智能控制理论研究液压变桨距控制系统。针对变桨距系统的非线性问题，也有学者将动态前馈补偿、滑模控制、反馈线性化技术、线性二次型最优跟踪控制理论等非线性控制技术用于变桨距控制系统研究，得到了较好的结果[5-9]。文献[10]则采用一步超前自适应预测方法，控制风力机转速和输出功率，这种方法对于具有大惯性特点的被控对象具有较好的控制效果。

最小方差控制方法是根据系统到当前时刻为止所有输入输出观测数据，来预测未来d步的输出（d为纯延迟），并根据预测输出设计当前控制作用。这种方法对于大滞后系统的控制是十分有益的，同时对于参数非线性和时变系统，也有一定的实用价值。本文首先介绍了风电机组变桨距系统的原理，针对变桨距系统特点和传统最小方差控制使用过程中存在的缺陷，提出了一种改进的最小方差控制方法，进而将改进的最小方差控制应用于某风电机组变桨距控制系统，进行仿真验证分析。

1 变桨距控制系统原理

根据风力发电机组运行特性，高风速下变桨距控制是根据风电机组输出功率的变化来控制变桨距机构调节桨距角，保证输出功率恒定，因此桨距角的变化量Δβ与风电机组输出功率的变化量有关，变桨距控制系统根据机组输出功率的偏差ΔP来计算桨距角的变化量，两者之间的关系定义为桨距角控制品质函数，它是桨距角和风速的函数，如（1）式表示[11]：

文献[11]给出了桨距角与控制品质函数之间的关系曲线如图1所示，图中描述了风电机组从额定风速12 m/s到切出风速24 m/s之间，不同风速下随桨距角变化情况。

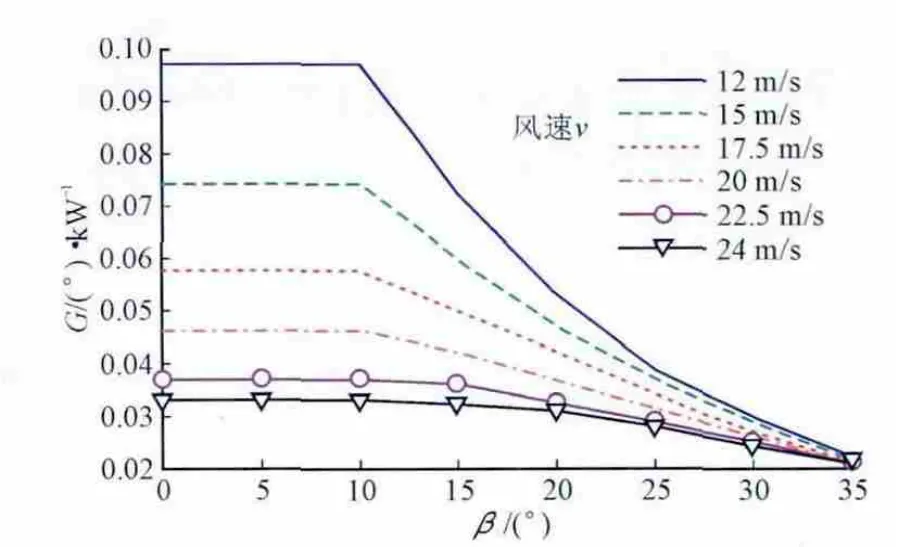
图1 桨距角控制品质函数Fig.1 Control quality function of pitch angle

根据实际测量风速v和桨距角β值按图1的函数关系获得桨距角控制品质函数G（β，v），并与风电机组输出功率偏差经PI控制器的输出量相乘，得到桨距角变化量Δβ。在当前桨距角β值基础上叠加角度变化量Δβ，即得到桨距角的指令值βcmd。

2 改进的最小方差控制

2.1 最小方差控制的数学描述

考虑被控对象采用CARIMA模型描述[12]：

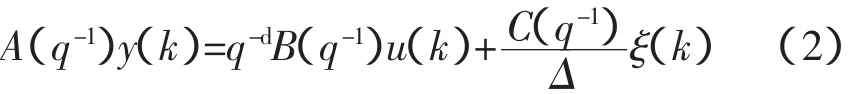
式中，k为当前采样时刻，d为对象的纯延迟时间，q－1为后移算子，Δ=1－q－1表示差分算子，ξ（k）为互不相nb，nc分别为多项式阶次，ai（i=1，…，na），bi（i=0，…，nb），ci（i=1，…，nc）分别为多项式系数，u（k）为当前时刻控制作用，y（k）为当前时刻输出信号。

到k时刻为止的所有输入输出观测数据对k+d时刻输出预测记为y（k+d|k），则使预测误差的方差J=E{y（k+d）－y（k+d|k）}最小的d步最优预测y*（k+d|k）可由下式给定：

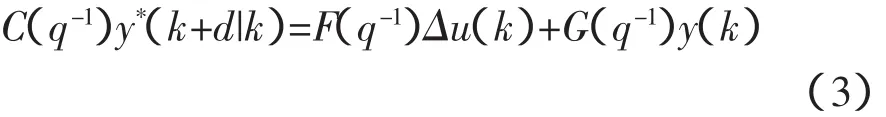
式中，F（q－1），G（q－1）可由Diophantine方程获得：

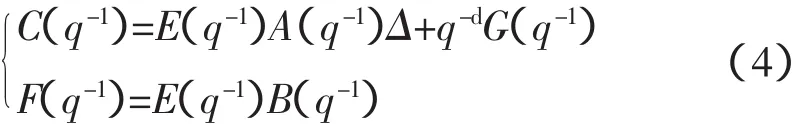
从而使实际输出y（k+d）与希望输出ym（k+d）之间误差的方差最小的控制律，即最小方差控制律可表示为

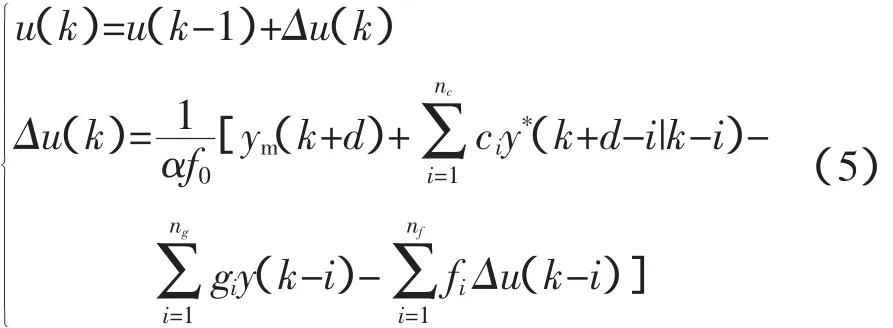
其中，当α=1，即为常用的基型最小方差控制律。可见，采用CARIMA模型描述被控对象，得到的控制律中含有积分作用，能够消除稳态偏差。

2.2 最小方差控制的不足与改进

2.2.1 最小方差控制的不足

最小方差控制算法简单，易于理解和实现，但是也存在着不足。首先，从式（3）、（4）可以看出，f0=b0，若b0过小，控制动作就可能过大，会加速执行机构的磨损或损坏。对于大惯性过程，在通过离散化方法获得CARIMA模型时，若采样时间选择不当，往往会得到较小的b0，控制作用可能过大是最小方差控制的一个基本缺点。

另外，从推导过程可以看出，该方法是根据对象纯延迟时间来确定最优预测，再根据偏差设计当前控制作用，不准确的初始条件、延迟时间的不确定、采样时间的选择等都可能显著影响最优预测，而使控制作用可能过大，控制过程发散。Clark等人提出的广义最小方差控制，在性能指标中引入了对控制作用的加权项，从而限制了控制作用剧烈的变化，只要适当选择性能指标中的加权项，还可以使非最小相位系统稳定[13]。但在使用过程中，加权项需要通过试探选择，选择不当仍达不到改进的效果。可见，最小方差控制存在的主要问题是在使用过程中控制幅度的限制，以兼顾稳定性和快速性。本文针对这个问题，进行适当改进。

2.2.2 延长预测步长

从最小方差控制控制律可以看出，由于对象存在d步延迟，控制作用滞后d个采样周期才能影响输出，因而提前d步对输出做最优预测，再根据预测输出与实际输出偏差最小来设计当前控制作用。实际上，在第d个采样周期时，系统尚未产生输入，当前的输入控制作用要在d的下一采样时刻产生作用。因而对有d步延迟对象作未来d步的最优预测存在较大误差，可能会使控制作用幅度过大。同时，在延迟时间未知，并对其估计不准确时，也很难确定预测步长。针对这种情况，可以考虑适当延长预测步长，对d+N步的输出做最优预测，并根据该预测输出设计当前时刻的控制作用。

2.2.3 时变αf0的设计

2.2.1 节中分析可知，较小的b0是使得控制作用可能过大的一个主要原因，从式（5）也可以看出，在控制收敛过程中，αf0的大小直接影响控制动作的大小，进而影响收敛速度的快慢。大的αf0能降低控制幅度但会延缓收敛过程，小的αf0能加快收敛过程但会增大控制幅度。根据控制幅度和收敛速度要求的侧重不同，αf0可适当偏大或偏小。但这种固定αf0的控制策略仅是一种单纯的折衷方案。通常情况下，最大控制幅度往往出现在突变过程的初期，因此αf0应设计为时变参数，在控制初期限制控制幅度，在控制后期加快收敛。文献[12]提出了限幅－收敛组合控制策略，本文采用其时变αf0的设计方法。

2.2.4 柔化控制作用

若最小方差控制律计算出来的控制作用记为ur（k），其将使系统输出y（k）在滞后d个采样周期的后一步达到其设定值ym（k），从而会引起输入ur（k）的大幅度变化，使得系统稳定性较差，在非最小相位系统中，还会引起输入输出的发散。如果将稳态时的控制作用us（k）直接作用到被控对象上，则输出y（k）跟踪ym（k）的过程变长，在牺牲快速性的情况下提高稳定性。文献[14]基于以上考虑，结合预测控制中的柔化思想，提出了实际控制作用u（k）在ur（k）与us（k）之间取其折衷的改进算法，即采用如下算式：

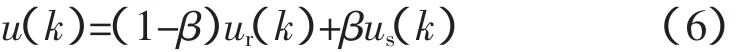
式中，β为输入柔化系数，且0≤β≤1。将折衷值u（k）作为实际的系统输入，可以通过选取不同的β值，保证被控对象的输出y（k）既具有一定的快速性，又具有较强的稳定性；而且在非最小相位系统中，仍能获得令人满意的控制效果。本文采用这种方法，并结合2.2.2节中延长预测步长的思想，将控制作用u（k）在uN1（k）和uN2（k）之间进行折衷的算法：

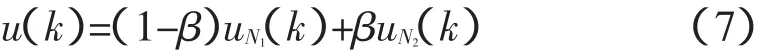
式中，uN1（k）和uN2（k）分别为根据d+N1步和d+N2步最优预测，采用最小方差控制律得到的控制作用。用uN1（k）取代ur（k）已在2.2.2节中进行了论述，uN2（k）取代us（k）可以进一步提高快速性。

2.2.5 自校正设计

以液压变桨系统为例，作为变桨距控制系统被控对象的液压伺服系统，包括比例阀控制器、比例阀、液压油管道、液压缸、活塞机构等，其中比例阀控制器、比例阀可以看作比例环节，液压油管道、液压缸、活塞机构等可视为纯惯性负载，并且活塞的左右面积不同，为非对称结构。可见，变桨距控制系统的被控对象参数很难精确确定，并且在动态过程中具有纯滞后、时变性等特点。因此，可采用在线辨识方法实时估计对象参数，实现自校正设计[11]。本文采用递推最小二乘辨识方法，递推方程如下：

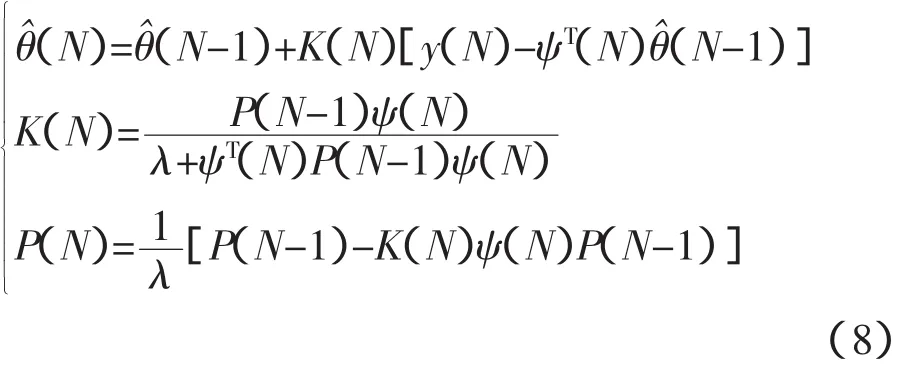
其中，θ和ψT（k）表示为

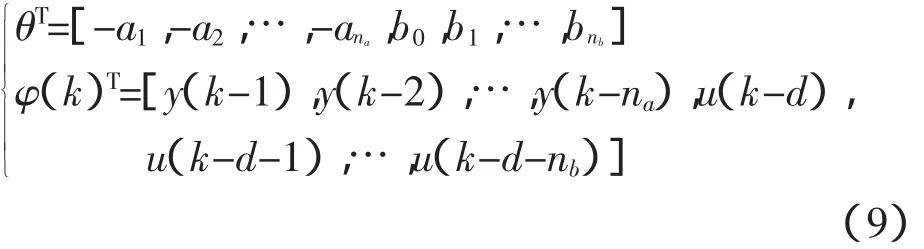
na，nb，nc与2.1节中定义相同，为模型阶次，d为被控对象纯延迟，θ赞是θ的估计值，λ是遗忘因子，0≤λ≤1。

根据变桨距控制系统工作原理和自校正最小方差控制算法实施步骤，得到基于改进自校正最小方差法的风电机组变桨距控制系统框图，如图2所示。

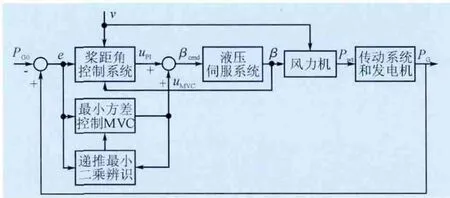
图2 采用最小方差法的变桨距控制系统框图Fig.2 Diagram of pitch angle control system using MVC

3 仿真分析

3.1 仿真对象

为验证改进的自校正最小方差变桨距控制方法的有效性，以某额定功率为300 kW的变速变桨距风电机组为例，仿真参数如下：风力机叶片长度R=15 m，转动惯量J=350 000 kg/m2，空气密度ρ=1.225 kg/m3，齿轮箱传动比1∶28.32，额定风速12 m/s，发电机额定功率Pg0=300 kW。

3.2 改进的最小方差控制器设计

1）时变的αf0根据输出的异常增量来及时准确判断过程的突变，然后经历一个由大变小的过程，以便在控制突发初期限制控制幅度，在后期加快控制速度。变化过程的端值和变化规律可以人为事先选定。本文设计的时变αf0的变化规律如图3所示，假设在5 s时刻，输出发生异常增量。

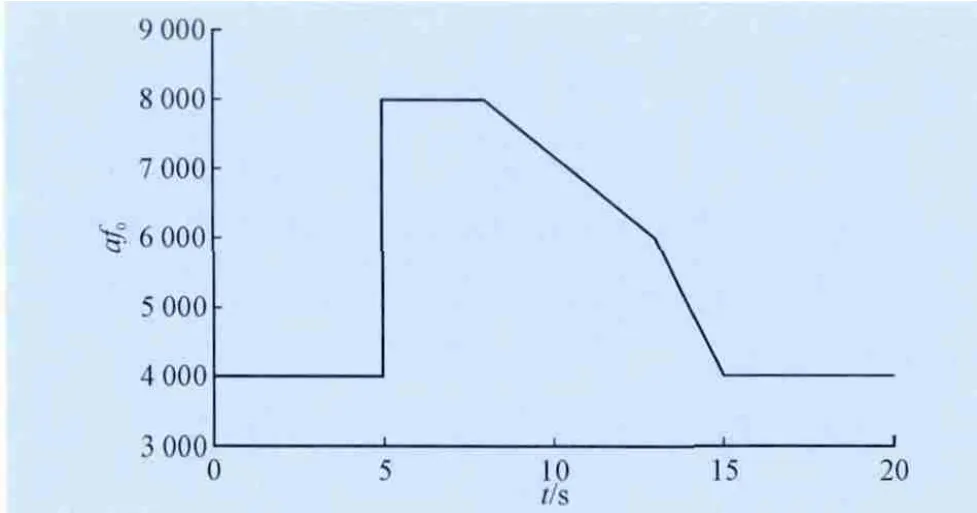
图3 时变αf0的变化规律Fig.3 Variation law of time-variableαf0

2）根据仿真对象的纯延迟步长，存在5倍采样周期的纯延迟，即d=5步，本文取延长预测步长d+N1＝30步和d+N2＝80步。

3）对以上根据d+N1步和d+N2步最优预测得到的控制作用进行加权折衷，作为当前时刻的控制作用输入，柔化系数ε取为0.6。

3.3 仿真结果

仿真模拟风电机组运行在额定风速12 m/s，输出额定功率300 kW。在20 s时，风速增加到18 m/s，风电机组开始执行变桨距控制，保持额定功率输出。图4为风速和风电机组输出功率变化曲线。

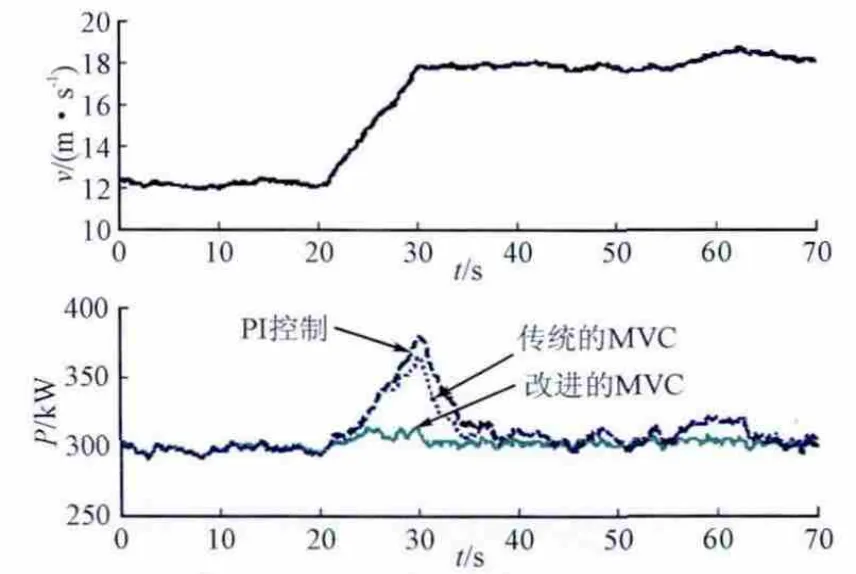
图4 风速与风电机组输出功率曲线Fig.4 Curve of wind speed and output power

从图中可以看出，风速在20 s时发生突变，增加到18 m/s，下图的输出功率变化曲线可以看出，采用改进的最小方差控制方法可以使风电机组输出功率相对于额定功率产生很小的偏差，在额定风速以上风速变化时较好的保持风电机组额定功率输出。另外两种常用的PI控制方法和传统的最小方差控制会在风速突增的开始时刻使得输出功率有较大升高，进而再通过调节偏差使得输出功率回到额定值附近，动态调节过程较慢。

图5为桨距角指令βcmd和实际桨距角β的变化曲线。可以看出，在风速突增的过渡过程中，改进的最小方差控制方法能够根据风速变化，快速计算获得变桨距的桨距角指令βcmd，驱动液压伺服系统调节叶片桨距角β快速响应，执行变桨距动作，从而实现限制风力机气动功率捕获，保证风电机组输出额定功率，使机组在高风速下安全运行。

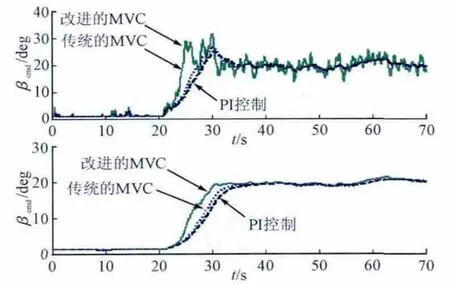
图5 桨距角指令βcmd和桨距角β变化曲线Fig.5 Curve of pitch command βcmd and pitch angleβ

4 结论

本文针对最小方差控制存在的不足，提出了延长预测步长的思想，并结合时变αf0设计和柔化控制作用，得到了一种改进的最小方差控制方法。该方法能够在突变过程初期，限制控制幅度，在控制后期能够加快收敛速度，能够得到很好的控制效果，弥补了传统最小方差控制的不足。

针对风电机组变桨距控制系统具有非线性、时变性及滞后性等特点，本文将改进的最小方差控制方法用于变桨距控制系统，通过仿真研究表明，与传统最小方差控制方法和PI控制及其改进方法相比，本文提出的方法使得系统响应迅速，动态偏差减小。

另外，改进的最小方差控制方法中时变αf0设计需要对实际情况有所了解，能够较为准确的判断输出异常和设计一个合适的αf0变化规律，这方面还需要进一步的研究。

[1] 邢作霞，郑琼林，姚兴佳，等.基于BP神经网络的PID变桨距风电机组控制 [J].沈阳工业大学学报，2006，28（6）：681-686.XING Zuo-xia，ZHENG Qiong-lin，YAO Xing-jia，et al.PID control in adjustable-pitch wind turbine system based on BPneural network[J].Journal of Shenyang University of Technology，2006，28（6）:681-686（in Chinese）.

[2]杨金明，吴捷.风力发电系统中控制技术的最新进展[J].中国电力，2003（8）：65-67.YANGJin-ming，WUJie.The latest development of control technology of wind power generation system[J].Electric Power，2003（8）:65-67（in Chinese）.

[3]王发达.基于神经网络PID液压驱动变桨距控制的研究[D].沈阳：沈阳工业大学，2007年.

[4] SHI K L，LI H.A novel control of a small wind turbine driven generator based on neural networks[C].Proceedings of IEEE Conference on Power Engineering Society General Meeting，2004（2），Piscataway N J，Denver，Colorado:1999-2005.

[5]HANSENAD，SORENSENP，IOVF，et al.Overall control strategy of variable speed doubly-fed induction generator wind turbine[C].Proceedings of Wind Power Nordic Conference，Chalmers tekniska h觟gskola，Goteborg，Sweden，2004:1-7.

[6] 秦斌，周浩，杜康，等.基于RBF网络的风电机组变桨距滑模控制[J].电工技术学报，2013，28（5）：37-41.QINBin，ZHOUHao，DUKang，et al.Sliding mode control of pitch angle based on RBF neural-network[J].Transactions of China Electrotechnical Society，2013，28（5）：37-41（in Chinese）.

[7] 何玉林，黄帅，杜静，等.基于前馈的风力发电机组变桨距控制[J].电力系统保护与控制，2012，40（3）:15-20.HE Yu-lin，HUANG Shuai，DU Jing，et al.Variable pitch control of wind turbine based on feed forward[J].Power System Protection and Control，2012，40（3）:15-20（in Chinese）.

[8]田艳丰，王哲，张纯名.大型风电机组多变量LQG最优独立变桨距控制[J].太阳能学报，2012，33（11）:2010-2015.TIAN Yan-feng，WANG Zhe，ZHANG Chun-ming.Multivariable LQG optimal individual pitch control of largescale wind turbine[J].Acta Energiae Solaris Sinica，2012，33（11）:2010-2015（in Chinese）.

[9] 崔双喜，王维庆，张新燕.基于反馈线性化的风力机变桨距最优跟踪控制[J].中国电力，2013，46（2）:93-97.CUI Shuang-xi， WANG Wei-qing， ZHANG Xin-yan.Variable pitch tracking control for a wind power system based on feedback linearization theory[J].Electric Power，2013，46（2）:93-97（in Chinese）.

[10]DADONE A，DAMBROSIO L，FORTUNATO B.One step ahead adaptive control technique for wind systems[J].Energy Conversion and Management，1998，39（5）:399-413.

[11]SENJYU T，SAKAMOTO R，URASAKI N，et al.Output power control of wind turbine generator by pitch angle control using minimum variance control[J].Electrical Engineering in Japan，2006，154（2）:10-18.

[12]李清泉.自适应调节器的收敛性和控制幅度 [J].清华大学学报，1986，28（6）：29-37.LI Qing-quan.The convergency and control magnitude of the self-tuning regulator[J].Journal of Tsinghua University，1986，28（6）:29-37（in Chinese）.

[13]CLARKE D W，GAWTHROPPJ.Self-tuning controller[J].Proceedings of the Institution of Electrical Engineers，1975，122（9）:929-934.

[14]金元郁，庞中华，崔红.改进的最小方差自校正控制算法[J].青岛科技大学学报，2005，26（2）：165-168.JIN Yuan-yu，PANG Zhong-hua，CUI Hong.Modified minimum variance self-tuning control algorithm[J].Journal of Qingdao University of Science and Technology，2005，26（2）:165-168（in Chinese）.