交通网络最优路径搜索的蚁群算法
2013-10-21周竹萍易富君
周竹萍 易富君
1.南京理工大学,交通工程系,南京 210094
2.招商局重庆交通科研设计院有限公司,重庆 404100
0 引言
动态最优路径搜索算法是智能交通系统(ITS)技术应用的关键问题之一。目前的路径诱导系统不够高效,在路径选择算法方面还不完善,缺乏实时性高、有效性强的路径搜索算法,故交通最优路径选择问题一直是各国交通领域投资研究的重点问题。
最优路径选择是指在给定的城市道路网中寻找一条从起始点到目标点之间的最优路径的问题。解决该问题的经典算法是Dijkstra 算法,是一种静态的局部最优算法[1]。该算法简单、易于实现,但也存在如下的局限性:在网络节点和路径较多的情况下,搜索效率会大大降低,有时甚至找不到最短路径,且对于路径权值随时间动态变化的动态网络,如反映路径堵塞和畅通信息的实时交通系统网络就不适用。
随着群智能技术的出现,基于群体仿生理论的蚁群算法为最短路径选择问题提供了一个新的解决方法。但是,由于蚁群算法本身的局限性,容易陷入局部最优解,且其道路信息素初始值固定,使算法收敛速度较慢[2]。近年来,我国学者提出了一系列的改进思路,如高尚、吴霜华等都考虑在蚁群算法中引入混沌理论[3-4],黄贵玲则在原始算法中加入直线优化启发信息,赵宝江提出了一种基于自适应路径选择和动态信息素更新的蚁群算法[5]。国外的重要研究包括:Guenther Fuellerer,Yuvraj Gajpal等也在信息素局部更新中加入几种其它启发式算法以提高算法效率,Alberto V.Donati 通过改进更新规则完成了两个及多个目标的优化[6-8]等。本文分析了传统蚁群算法的不足,改进了信息素更新方式,使算法更满足求解交通系统的最优路径问题。
1 问题概述与模型
如果把城市道路网中的道路起始点、目标点和交叉路口等表示为节点,把道路表示为连接节点的弧(边),把道路的长度、通行时间和拥塞程度等属性表示为弧的权,那么道路网就可以被抽象成为一个带权的有向图,如图,1 所示。
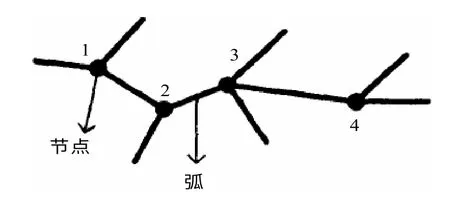
图1 由节点和弧构成的有向道路网络图Fig.1 Traffic network composed of nodes and arcs with direction
在赋权有向图G 上,一条以i 为始点,j 为终点的路径是一个弧的序列,其中前一个弧的终点是后一个弧的起点,且第一个弧的起点是i,最后一个弧的终点是j,可用一个有序的点集来描述一条路。一条路的费用是这条路径上所有弧的费用之和。用赋权有向图来表示路径的费用即为该赋权有向图中这条路径上所有路径权值之和。
给定带权有向图G=(V,{E}),其中V 是包含n个顶点的顶点集,E 是包含m 条弧段的集合,<v,w>是从v 到w 的弧,c(v,w)是弧<v,w>的非负权值,设 vs,vt为V 中的顶点,Pst={vo=vs,v1=,…,vn=vt}为V 中由vs到 vt的一条路径,则路径 Pst的权值总和TW(Pst)可表示为[9]:

最优路径问题就是指在带权有向图中,寻找从指定起点到终点的一条具有最小权值总和的路径问题,即寻找一条路径使得TW(Pst)最小。
在交通路网最优路径选择中进行路径选择并不完全同于在赋权有向图中求最短路径问题的方法。在实际的交通中,路段的流量实时变化,单向行驶、交叉口转向限制等也越来越复杂。伴随着不同的实际应用目的,最优路径规划中也有很多优化标准,如最短行车距离、最少行车时间、最低费用等。同时还要求有较快的速度和较高的效率。这就对最优路径选择算法本身提出了一定的要求。只有选择合适的算法才能找到满足条件的最优路径。
2 蚁群算法原理与模型
2.1 基本原理
蚁群优化算法(简称蚁群算法),1991 年由Marco Dorigo 和他的同事1991 年首先提出[10-11]。作为一种多agent 的方法,较好地解决了一些复杂的组合优化问题,如 TSP(Traveling salesman problem)问题以及指派问题。蚁群算法主要模拟蚂蚁的食物搜索行为,当蚂蚁在食物源和巢穴之间行走时,会在路上存储信息素。蚂蚁可以感知到环境中该物质的存在及其强度,并在选择移动时,倾向于选择信息素浓度高的方向。当某条路径较短时,会有较多的蚂蚁使用这条路径,使得该路径上被存放较多的信息素,从而吸引更多的蚂蚁使用这一路径。最终,信息素浓度最高的路径标志出食物源和巢穴之间的最短路径。
2.2 基本模型
以求解平面n 个城市的问题(用(0,1,…,n-1)表示城市序号)来说明基本蚁群算法。引入如下记号:m 为蚁群中的蚂蚁数;dij为城市和城市之间的距离;τij(t)为t 时刻路径(i,j)上的信息量,n为城市的数量。
初始时刻,各条路径上的信息素相等,设τij(0)=C,(C 为常数),蚂蚁 k(k=1,2,…,m)在运动过程中根据各条路径上的信息素量决定转移方向。基本蚁群算法所使用的状态转移规则被称为随机比例规则,它给出了位于城市i 的蚂蚁转移到城市j 的概率。为在t 时刻蚂蚁k 由城市i 转移到城市j 的状态转移概率:

式中:
α——蚂蚁在行进过程中所积累的信息素浓度对它已选择路径所起的作用大小,当α=0 时,算法就是传统的贪心算法;
β——ηij的重要程度,当β=0 时,算法就成了纯粹的正反馈的启发式算法,可通过试验来确定参数α,β 的最优组合;
ηij——由城市i 转移到城市j 的期望程度,可根据某种启发式算法而定,例如,可以取
Ak——蚂蚁k 下一步允许走过的城市的集合,它随蚂蚁k 的行进过程而动态改变。
蚁群在觅食过程中,一方面通过蚂蚁的行走会在路径上留下新的信息素,另一方面随着时间的推移已有的信息素会逐渐挥发,所以,各条路径上的信息素会根据蚁群的行动和时间变化不断更新。经过n 个时刻,蚂蚁k 可走完所有的城市,完成一次循环。此时,要根据下式对各路径上的信息素浓度作更新:
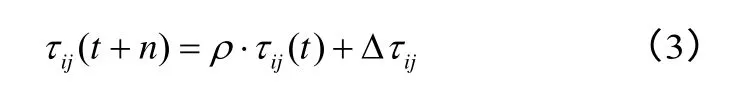
式中:
τij(t)——随时间的推移会逐步衰减;
ρ——信息素挥发参数,其作用是使个体蚂蚁忘掉过去从蚁群搜索过程中获得的一部分经验,避免过早收敛于一个局部最优解[12],用1-ρ 表示它的衰减程度;
Δτij——路径上信息素浓度的变化量,

式中,Δτijk表示蚂蚁k 在本次循环中在城市i 和城市j 之间留下的信息素浓度,其计算方法根据计算模型而定。
Dorigo Macro 曾给出了不同的蚁群算法模型,分别称为 ant-cycle 模型(亦称蚁周系统模型)、ant-quantity 模型(亦称蚁量系统模型)和ant-density模型(亦称蚁密系统模型),它们的差别在于Δτijk(t)的求法不同[13-14]。蚁密系统模型信息素增量为固定值 Q;而在蚁量系统模型中,信息素增量的值为,与路径(i,j)的长度有关;在蚁周系统模型中,信息素增量为,它与具体的 dij无关,只与 Q和搜索路线有关。这3 种模型中,ant-cycle 模型最适用于最短路径问题[8]。在ant-cycle 模型中:

式中:Q 是信息素强度,它影响算法的收敛速度;Lk是第k 只蚂蚁在本次循环中所走路径的长度。
2.3 采用蚁群算法求解最优路径的可行性
蚁群算法本质是一种并行的算法。蚂蚁搜索的过程彼此独立,只通过信息素进行间接的通讯。由于大规模的并行计算,可以显著减少计算时间。它是一种正反馈算法。正反馈的存在,使得搜索收敛速度加快。它很容易与多种启发式算法结合,以改善算法的性能。它具有较强的鲁棒性。对算法模型稍加修改,便可以应用于其他问题。
蚁群算法已被成功地应用于许多可表达在图表上寻找最佳路径的问题。交通系统的最优路径选择与蚂蚁觅食行为类似。将车辆的起始点看作蚁巢,目的地看作是蚂蚁所要寻找的食物源,车辆在从起始点开始经过一些路段、节点,最终到达目的地在路径选择的过程中,个体车辆根据本身的判断选择所需要的路径行驶。在这里整个路网就是一个有向图,车辆就是具有智能行为的人工蚂蚁,并且该人工蚂蚁只是找到从起始点到终止点的路径,并不返回到原来的起始点[15]。通过对交通过程的抽象,将交通中实际的耗费作为启发信息,这样可以建立起一个进行最优路径选择的人工蚁群系统。
3 基于信息素更新方式改进的蚁群算法
为了克服基本蚁群算法的缺陷,通过自适应地改变算法的信息素更新方式,可以在保证收敛速度的前提下提高解的全局性;通过改进路径选择策略和模型,可以使该算法更符合交通网络的运行规律,提高算法的自适应能力。
3.1 信息素限定原则
引入信息素限定规则,将每条边上的信息量限定在[τmin,τmax]之间,即为Max-Min Ant System 的主要思路。设置了信息素强度的下限 τmin,所以选择某些边弧的概率虽然可能性非常小,但永远不会为零,这样就减少了停滞行为出现的机会,从而使蚂蚁能进行更高程度的搜索;因为基本蚁群算法在寻找最优路径时,并不像交通规划一样要考虑路网的承受能力,因此,改进的蚁群算法中也设置了信息素强度的上限 τmax,使得这两者信息素的差别不会趋向于无穷大。
3.2 信息素局部更新算法的改进
道路网络中还存在这样的特性:某条路径的出行时间会随着交通流量的增加而增加。因此,将蚂蚁行走过程中的信息素更新方式设置为局部更新原则。局部信息素更新的作用是使已选的边对后来的蚂蚁具有较小的吸引力,从而使蚂蚁对没有被选中的边有更强的探索能力。实验表明,局部更新规则可以有效避免蚂蚁收敛到同一路径[16]。MMAS为TSP 问题的解决提出了信息素轨迹平滑机制,让轨迹浓度的增加与最大浓度 τmax和当前浓度 τij之间的差值成正比。信息素轨迹平滑机制较好地考虑了交通网络中路径的不同状态特性,但是,计算较为复杂。本文采用了平滑机制的思路,根据不同状态设置不同的模型形式,简化为用分段函数表示。当蚂蚁从城市i 转移到城市j 后,路径(i,j)上的信息素量按下式进行更新:
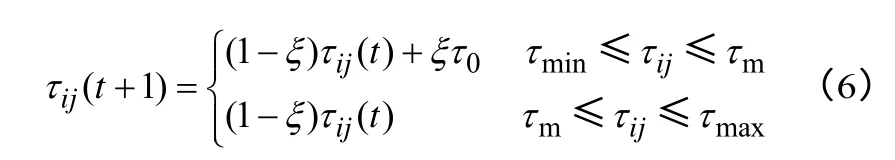
式中:ξ∈[0,1]的一个参数;τ0为一个很小的数,经验观测值为;n 为城市数目;Lbest为该次循环中最短路径长度;τm为临界值,反映系统的状态,根据具体的实验情况而定。
3.3 信息素全局更新模型的改进
蚂蚁根据信息素留下的多少选择路段,而当所有蚂蚁都选择某路段时,可能造成某路段的负荷过大,形成所谓的交通拥堵现象。虽然,在前述的局部信息修改的过程中考虑了路网容量的特性,但当交通拥堵越严重,根据ant-cycle 模型公式(5)可得蚂蚁在路网上留下的信息量仍然是最大的,即其它的蚂蚁根据公式(2)继续选择该路段,最终造成该路段崩溃[17]。现有研究较多的是对公式(4)做必要的调整,引进路段上的阻抗函数。由于本文讨论的是动态最优路径搜索问题,所以要引进能反映实时路况的广义路阻来计算[18]。广义路阻是在各种因素(如路段平均行驶速度、车辆行驶的通畅性、路段拥挤度、路口排队长度和平均延误等)影响下,路段行驶时间和路口延误的综合表征量。路段(i,j)上的广义路阻 T(i,j)计算式为:

式(7)中,t(i,j)为路段(i,j)的行驶时间;r(i,j)为在路段(i,j)上的车辆平均延误。式(8)中,t0(i,j)表示交通流为零时路段(i,j)的行驶时间;V 为路段交通量当量值;C 为路段实用通行能力;k1、k2分别为回归参数,根据道路交通量、车速调查数据用最小二乘法确定。式(9)中,r1为均匀延误,r2为过饱和延误,即随机到达的增量延误所引起的附加延误:其中,k3、k4为常数;T 为周期长度;λ 为进口道绿信比;X 为交叉口饱和度;C 为进口道实用饱和通行能力;S 为路口影响修正系数。
所以,在全局信息素更新规则中公式(5)改进为:

式中,T(i,j)是路段(i,j)上的广义路阻。
式(10)作为信息素更新规则可以使广义路阻较大的路段获得的信息素更新量较小。
在广义路阻的基础上,运用该算法可以完成最优路径规划的多种优化标准要求,如最短行车距离、最少行车时间、平均车速、最低费用等。
4 计算机仿真实验
4.1 实验算法
根据蚁群优化算法的思想,本文的最优路径搜索过程分几步进行:首先,初始化起始节点、终止节点和交通量,确定循环次数,让一定数量的人工蚂蚁的每个蚂蚁代表一定的交通量并分批置于交通出行始点上进行循环,初始循环可以随机地让人工蚂蚁进行路径的选择。每循环一次人工蚂蚁根据上一次循环信息素轨迹分布概率进行路径的选择,逐个在路网上移动,从起点到达终点的蚂蚁成功完成一次循环,并在相应路径上留下成功的信息素轨迹,局部更新轨迹强度,并检查信息素数量是否处于规定的范围之内。然后,当一批蚂蚁完成循环后,寻找最优路径,再对轨迹强度全局更新。至此,完成了一次最优路径搜索。最后寻找全局最优解,即到当前迭代次数为止。在所建立的所有局部最优解中,值最小的解作为当前迭代次数的全局最优解。当有足够的蚂蚁数量和循环次数,交通系统将向平衡分配方向发展,结果亦更加趋近于最优解。
针对本文将要解决的实际的动态交通路径问题,给出蚁群算法进行路径选择的算法步骤如下:
Step 1 信息初始化 初始化将蚂蚁逐个放置于起点;初始化α,β,k,tmax,τij(0),m,Q等系数。其中 tmax为最大迭代次数。
蚁群算法中的参数设定目前尚无理论上的依据,参数Q,C,α,β,ρ 可以用实验确定其最优组合。经验结果为:1≤α≤5;1≤β≤5;0.5≤ρ≤0.99,ρ 取0.7 左右为佳;1≤Q≤10000[19]。
Step 2 选择原则 对每只蚂蚁用转移概率在禁忌表中没有的汇点中选择要移动的下一个汇点,位于第i 个节点的蚂蚁k,按(3)式选择策略选择边(i,j)。将所选汇点放入禁忌表每只蚂蚁环游一圈后,计算这只蚂蚁在此环游路径的综合系数值。
Step 3 局部更新原则 当蚂蚁选中边(i,j)后,就更新边(i,j)上的信息量,即每当蚂蚁选中一条边后,就按(7)式更新减少边上的信息量,从而增加蚂蚁选择其它边的概率。
Step 4 局部搜索 当m 只蚂蚁从起点到终点搜索完后,则求得m 个解。为了尽可能遍历所有解,分别在这些解的邻域中,采用局部搜索算法,求出局部最优解。
Step 5 全局更新原则 当所有的m 只蚂蚁都得到局部最优解后(否则跳入Step2),按照(4)、(5)、(11)式全局更新信息量,即全局更新路段流量,更新路段阻抗。比较所有环游得出的系数值,找出最好的环游路径。
Step 6 求全局最优解 到当前迭代次数为止,在所建立的所有局部最优解中,值最小的解作为当前迭代次数的全局最优解。
Step 7 不断迭代直到满足停止的条件。
4.2 算例仿真
给定一个如图2 所示的路网,为简化计算,路网直接标定了实时的广义路阻值(边上的数字),求该时刻从起点①到终点⑭在该时刻的最优路径。
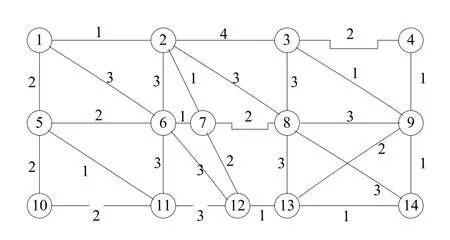
图2 示例的路网Fig.2 Example network
按照4.1 中的算法步骤进行计算,参数取值见表1。在软件Matlab 7.0 环境下实现,迭代5 次即搜索到了最优路径:①→②→⑦→⑫→⑬→⑭。说明本文改进的蚂蚁算法因其本质并行特性用于路径寻优中具有较高搜索效率和一定准确性,能够实现快速的全面寻优。

表1 参数值Tab.1 Parameter values
与基本蚁群算法相比,改进后的算法的探索新路径点则是在局部更新规则的作用下出现的,算法经过一定的循环次数后收敛于一个最优解,为避免此最优解为局部最优解,在局部更新规则的作用下,不断地减少此最优路径上的信息素,从而促使蚂蚁跳出局部最优解,寻找一条新的路径。在算法的准确度和效率方面,本文的算法也有优势。
另外,文中给出的示例网络不算复杂,很快就能搜索到正确的最短路径。当交通网络相对比较复杂时或者是动态变化时,虽然可能在规定的较短时间内搜索不到最短路径,但可通过迭代的方式,在较少迭代次数下搜索到的“次优”路径将也能够避开交通稠密地区,满足路径诱导要求。而且对于动态路径诱导。该算法对目标函数、初始数据和模型复杂程度均无特殊要求,特别是当目标函数为非线性时,其优势更为明显,因此更适用于动态最优路径的搜索。
5 结束语
本文尝试用蚁群算法来求解最优路径选择问题,并根据交通网络的要求对基本模型进行了改进,且通过实验仿真取得了较为满意的效果。同时也证明了该方法具有一定的理论参考价值和实际意义。将蚁群算法应用于交通网络最优路径的选择过程中,能充分发挥算法的协作性、正反馈和分布式并行计算的特点。但由于蚁群算法的发展还在起步和探索阶段,目前仍存在一些待研究的问题,如算法的收敛性、参数的合理设置及如何降低时间复杂度等。而且,对于动态交通网络中如何应用蚁群算法,如何通过迭代的方法求出最短路径,也是值得进一步深入研究的问题。但是,可以肯定的是,随着蚁群算法的深入开展,它必将成为交通规划和交通组织网络化的优化算法,从而促进整个交通网络优化的发展。
[1]殷 超.基于改进Dijkstra 算法的最短路径搜索仿真[J].山东理工大学学报(自然科学版),2010,24(6):33-36.
[2]黄贵玲,高西全,靳松杰,谈飞洋.基于蚁群算法的最短路径问题的研究和应用[J].计算机工程与应用,2007,43(13):233-235.
[3]高 尚.解旅行商问题的混沌蚁群算法[J].系统工程理论与实践,2005,(9):100-104.
[4]吴霜华,付 洋,葛 亮,基于混沌蚁群算法的最短路径选择研究[J].重庆交通大学学报(自然科学版),2007,26:126-128.
[5]赵宝江,李士勇,金 俊.基于自适应路径选择和信息素更新的蚁群算法[J].计算机工程与应用,2007,43(3):12-15.
[6]Fuellerera Guenther,Doernera Karl F.,Hartla Richard F.,Iorib Manuel.Ant colony optimization for the two-dimensional loading vehicle routing problem[J].Computers &Operations Research,2009,36(3):655-673.
[7]Yuvraj Gajpal,PrakashAbad.An ant colony system(ACS)for vehicle routing problem with simultaneous delivery and pickup[J].Computers &Operations Research,2009,36(2):3215-3223.
[8]Donati Alberto V.,Montemanni Roberto,Casagrande Norman et al.Time dependent vehicle routing problem with a multi ant colony system[J].European Journal of Operational Research,2008,185(3):1174-1191.
[9]Sheffi Yosef.Urban transportation networks:equilibrium analysis with mathematical programming methods[M].New Jersey,USA:PRENTICEHALL,INC.,1985.
[10]Dorigo M.Optimization,learning and natural algorithms[D].Milano,Italy:Dipartimento di Elettronica,Politecnico di Milano,1992.
[11]Dorigo M.,Gambardella L.M.Ant colony system:a cooperative learningapproach to the traveling salesman problem[J].IEEE Transactionson Evolutionary Computation,1997,1(1):53-66.
[12]陈小强,杜呈欣,熊伟清.蚁群算法求解函数优化中的参数设置[J].计算机工程与应用,2008,44(17):53-55.
[13]Bonabeau E.,Dorigo M.,Theraulaz G.Inspiration for optimization from social insect behavior[J].Nature,2000,406(6):39-42.
[14]靳凯文,李春葆,秦前清.基于蚁群算法的最短路径搜索方法研究[J].公路交通科技,2006,3(23):128-134.
[15]夏立民.交通系统中最优路径选择算法的研究[D].北京:首都师范大学,2007.
[16]方丽君.基于蚁群算法的交通分配模型研究[D].南京:河海大学土木与交通学院,2006.
[17]王 勇,雷 黎,纪寿文,赵 琳等.基于改进蚁群算法的交通分配研究[J].公路交通技术,2007,6(3):159-161.
[18]陆 骏,王小平,曹立明.一种基于蚁群算法的车辆导航系统模拟模型[J].计算机应用与软件,2005,22(4):17-19.
[19]马 良.全局优化的一种新方法[J].系统工程与电子技术,2000,22(9):62-64.
