基于货物时间价值的物流网络最优配送路径模型研究
2013-10-21陈文强顾玉磊
陈文强 顾玉磊
长安大学,经济管理学院,西安 710064
0 引 言
在物流配送网络中,物流配送商如何按照一定的规则选择最优路径,完成物流需求配送工作,一直是研究者的重要课题,研究成果丰富。例如,H.C.Joksch[1]提出一类带有时间约束的最短配送路径问题,并给出了静态的规划方法;G.Handier[2]提出了边带成本约束的最短配送路径问题,并证明其属于NP 完备问题,并给出了一个对偶算法;J.More等[3]提出了一个双目标最短配送路径问题,并给出了算法。上述模型一般为定常需求模型或为静态路径模型,其对中长期物流配送网络的规划是有效的。但是,在现代物流网络中,由于交通事故、道路拥挤、天气变化等偶发因素常引起物流配送网络的动态变化性(OD 对之间的最优路径是时变的),因此,利用传统静态最优配送路径模型研究实际问题时,容易导致决策错误[4]。基于此,本文充分考虑了动态出发时间和运输过程延迟对配送路径选择的影响,提出了基于时间、费用的双目标决策的动态物流网路配送最优路径模型。
1 问题分析
1.1 问题表述
本文所述物流配送网络是基于城市道路网组成的物流网络,由运输路径,物流配送节点组成。基于物流配送需求特点,将物流运输网络进行抽象。物流配送网络被抽象为矢量图,物流配送节点是图中的节点,运输路径是图中的线,配送方向与物流方向一致。图1 是一个典型的物流配送网络几何抽象图g,由配送网络节点N、运输路径A 和时间T 构成,此图也可以用函数G=f(N,A,T)表示。如何在物流配送网络g 中,符合实际地选取基于动态时间和费用的最优配送路径O-D(从O 点到达D点)是本文的基本问题。
1.2 问题的解决思路
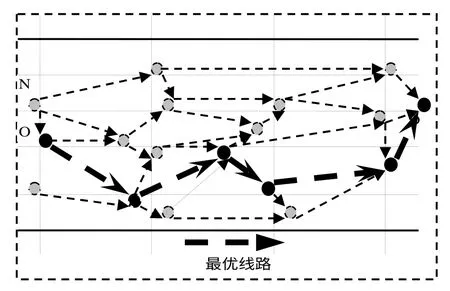
图1 典型物流配送网络抽象Fig.1 A typical distribution network
多目标最优配送路径问题的一般处理方式是把多目标转化为单目标去求解[5],从而使时间、费用相关的最优路径转化为单目标最优路径问题。物流配送需求实现过程由运输过程和装卸过程两部分组成,所以,本文采用两阶段分析法,把最优路径问题分为两个部分,建立各自模型,最后联合分析求解总目标(费用最小路径)。
2 模型构建
配送过程中,最优配送路径选择往往是由多种因素决定的。但时间和费用一般是决定最优配送路径的主要影响因素,并且,影响效果一般通过实际配送费用来计量[6]。由于物流需求的异质性,同一种服务反映的实际费用会有所不同。为清晰反映实际费用构成,本文把实际费用分为客观费用和货物时间价值损失。所谓货物时间价值的损失,是指物流需求没有在规定时间内到达目的地,使货物失去一定时间价值。它可用两个参数乘积(前提假设,时间价值是在途时间和时间价值损失系数的线性函数)来表示,即货物在途时间与货物(出行时间和配送延迟)时间价值损失系数乘积。
物流配送需求实现全程由运输过程和装卸过程两部分组成,实际费用也可以分为运输过程费用和装卸过程费用。
2.1 运输过程费用模型函数
运输过程费用由运输客观费用和运输时间价值损失组成,运输客观费用也可称为运输过程的固定费用(燃料、人工、损耗等),它是由运输技术经济特性决定的;运输时间价值损失是货物对运输时间延迟的价值缺失表现,用运输过程时间*货物运输时间价值损失系数来表示。那么,运输过程费用可用函数(1)表示。

αm(t)——出发时间为t 的m 类物流需求运输时间价值损失系数(运输造成的时间价值损失系数定义如下:在规定的时间内将货物运到目的地,运输时间价值损失系数为零。距离货物失去时间价值的时间越远,由于运输造成的时间价值损失系数越大)。
2.2 装卸过程费用模型函数
如运输过程费用一样,装卸过程费用也分为装卸过程固定费用(客观费用)和装卸过程时间价值损失。装卸过程固定费用由像装卸费、人工等相关固定费用组成;装卸过程时间价值损失是由于装卸时间延迟等而造成货物价值的损失,用装卸过程时间乘以装卸时间价值损失系数表示。装卸过程相关费用函数如(2)所示。
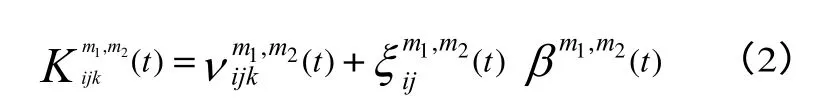
2.3 最小费用路径模型函数
在物流配送网络中要想找出最小费用路径,物流配送需求实现费用模型必须计算经由每一个节点的运输相关费用和装卸相关费用。根据这一原则,整个运输过程费用模型函数设计如式(3)所示。
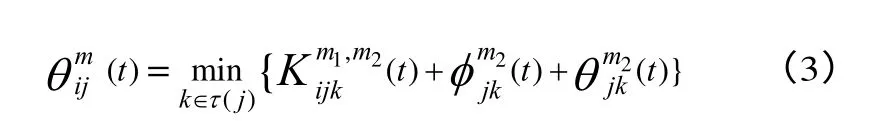
此模型最明显特征就是把整个配送过程的固定配送费用和时间价值损失很直观的联系起来,并且可以清楚的表明整个配送过程实际费用的明细。
3 模型求解
3.1 算 法
最小配送费用路径求解采用倒推法由终节点D向前推进[7],具体步骤如下。
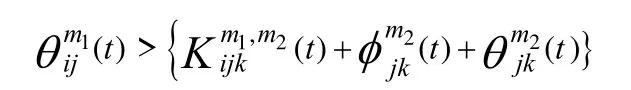
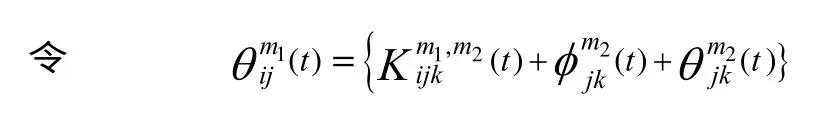
则节点k 为最优路径的一个节点。
(2)重复步骤(1),找出k 节点的上一个最优路径节点τ-1(k);
(3)重复步骤(2),直到找出最优路径的所有的节点;
(4)结束算法。
此算法从终节点向前推进,算法过程其实就是检查一个节点k 前一个节点τ-1(k)是否存在一条路径使节点k 到τ-1(k)的费用最小,如果条件满足,τ-1(k)是条件点之一。依此类推,直到找出所有符合条件的节点,这些点组成的路径就是基于时间相关的物流网络最小配送费用路径。
为保证算法的合理性,必须对参数进行合理设置。
3.2 正确性检验
如果目标函数值为有限数,则目标函数形式为
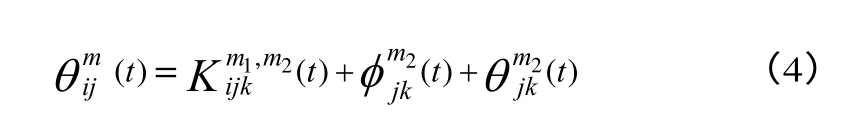
且必满足下几种情形之一。
如果是情形①或②或③发生,则进入算法步骤(2);
如果发生情形④且j≠D,则目标函数为

那么进入算法步骤(1)。
无论模型算法还是正确性检验,均可以在计算机环境下自动实现。
4 实例证明
假设物流配送网络如图2 所示,从O 点出发进行物流配送,D 点集结补养,综合考虑运输相关费用和装卸相关费用,求解最佳配送路径。利用Netlog软件,编写程序,模拟运算,结果如下图(黑粗线)所示。
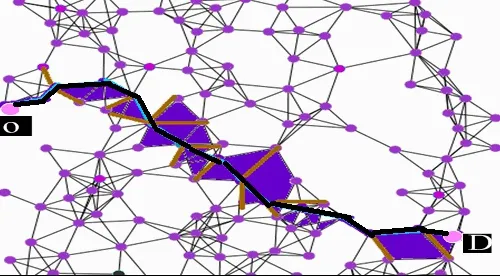
图2 最优物流配送路径Fig.2 The optimal logistics path
图例中黑色区域是备选路径和节点组成的三角网络,黑粗连接线表示算法选择路线,即最优配送路径。
5 结束语
本文根据物流配送网络中影响物流配送的的诸多因素,构建了基于货物时间价值的物流网络最小配送费用路径模型,依据物流配送的决定因素是实际配送费用,从而将多目标最优路径转化为最小配送费用路径问题,给出模型的算法,验证了算法的正确性,论文最后利用Netlog 软件检验了模型的正确性,结果显示,模型及算法是可行的。
[1]Jokson H.C.The shortest riute problem with constraints[J].Journal of Mathematical Analysis and Applicatilon.1996,(14):191-197.
[2]Handier G.A dual algorithm for the constrain shortest path[J].networks.1980,10(20):293-310.
[3]MORE J.,Murthy I.A parametric approach to solve constrain shortest path problem[J].European Journal of Operation Research.1991,53:81-92.
[4]Newall G.F.Flow on transportation network[M].MIT Press.1980.
[5]Ziliaskopoulos A.K.and Wardell W.An intermodal optimum path algorithm formultion modal networkswith dynamic arc travel times and switching delays[J].European Journal of Operational Research.2000,125:486-502.
[6]Jourquine B.and Beuthe M.Transportation policy analysis with a geographic information system[J].The Virtual Network of Freight Transportation in Europe,Transportation Research.1996,4C:359-371.
[7]陈文强,吴群琪.时间相关的运输网络最小费用路径模型及算法[J].铁道运输与经济.2009,5(31):11-14.
