基于路网二次分层模型的出行路径诱导优化方法
2013-10-21潘大为季彦婕
潘大为 邓 卫 季彦婕
1.扬州市公路管理处,扬州 225000
2.东南大学,交通学院,南京 210096
0 引 言
国民经济的快速增长、城市化进程的加快、道路交通条件的改善带来了机动车保有量的显著增加,居民出行方式的机动化趋势日趋显著,由此所产生的城市交通问题也日益突出。路径诱导系统作为智能交通系统的重要组成部分,在解决拥堵问题时将发挥关键性的作用。
目前,出行诱导路径算法比较多,最基本的算法是Dijkstra 算法[1],在此算法改进的基础上,产生了边带标号的最短路算法、A*搜索算法[2,3]、高速路分层算法[4]等。王海梅等[5]采用矩形限制区域搜索算法来提高算法的效率和精确度;吴成中等[6]应用神经网络对交通信息进行实时预测,构造具有时变性的路阻矩阵,并与限制搜索区域的算法结合,解决了算法的实时性差、收敛慢等问题;王亚文等[7]借助图像学知识,利用路网的多比例尺数据对不同等级道路进行分层,用于降低搜索路网的复杂度,提高运算效率。但是,实际的路网规模大,路况复杂,结合已有研究成果,在深入了解路网结构以及道路交通状况的基础上,建立路网二次分层模型,利用路网不同层之间的协同,提出优化的出行路径诱导方法。
1 路网二次分层模型的建立
1.1 基于路网结构的初分层
从宏观角度对路网进行初分层,即从城市路网的功能结构、等级结构以及布局结构方面进行综合考虑。表1 为路网功能、等级以及布局结构比较。

表1 路网功能、等级以及布局结构比较Tab.1 Comparative amony road network’s function,grade and layout
初分层满足以下几个条件:
(1)层数小于等于路网等级分类数,各层的路段数接近。
城市路网快速路较少,而且与主干路功能类似,将这两种道路划为同一层,因此,总层数P≤3层,各层路段数Q 大致相等。
(2)满足道路等级的结构要求,相近等级道路相对集中于同一层。
相邻等级道路可以合并到同一层,例如主干路可以与次干路合并,次干路可以与支路合并,但是主干路不宜与支路合并。
(3)满足道路功能的结构要求,通过性、可达性类似的道路相对集中于同一层。
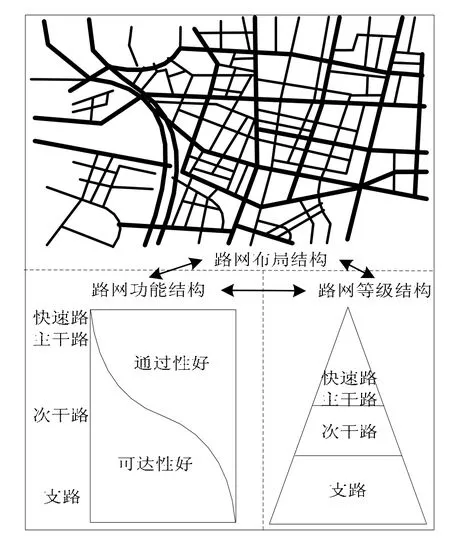
图1 路网功能、等级以及布局结构Fig.1 Structure of road network’s function,grade and layout
假设按照功能结构中通过性与可达性的强弱,将各个路段从1 到10 赋值,其中赋值1 代表路段的通过性最好,可达性最差;赋值10 代表路段的可达性最好,通过性最差。依据各层路段的功能构成赋予a 层b 路段的权值为 rab,其中a 为路网层编号,b 为路段编号,a≤P,b≤Q,满足
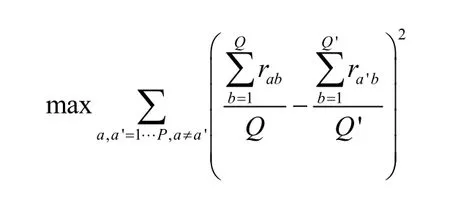
(4)满足道路布局的结构要求,依据不同布局所体现出的交通流分布规律对路网分层。路网布局影响交通流的分布,路网分层要考虑流量分布的影响。
1.2 基于路网交通状态的次分层
路网由路段以及路口组成,通过路段及路口状态描述路网交通状态更加合理。m 个路口和路口间的路段组成的路网,其路口集合表示为N={n1,n2,…nm};路段集合表示为 L={lij≤ni,nj>};其中,i,j=1,2,…,m。路网交通状态次分层引入如下两个变量和四个矩阵:
变量1:路段交通状态系数 sij
路网交通状态系数为路段 lij在某个交通数据采样时段内单位长度上的平均行程时间sij=Tij/dij=1/vij,其中 dij为路段 lij的长度,vij为采样时段路段平均行程速度。路段交通状态系数综合考虑了路段平均行程时间和路段长度,把计算路段行程时间转化为计算路段平均速度。
变量2:路段拥挤程度值λ
路网拥挤程度值λ 为不同拥挤状态对应速度v的倒数,即λ=1/v。在进行交通状态分析时,在拥挤程度值区间制定一个交通拥挤值作为交通拥挤程度截值 λr来评价交通状况。根据中国道路交通管理评价指标的规定:城市主干道机动车平均行程速度不低于30km/h 为畅通,20km/h~30km/h 之间为轻度拥挤,10km/h~20km/h 之间为拥挤,低于10km/h 为严重拥挤。依此标准,可以选取交通拥挤程度截值,例如,可以取 λ1=0.1,λ2=0.2 作为严重拥挤程度截值;λ3=0.066,λ4=0.05 分别作为拥挤程度截值;λ5=0.04,λ6=0.033 作为轻微拥挤程度截值。
矩阵1:路口邻接矩阵 k={kij},此矩阵表示路网之间物理连接关系:
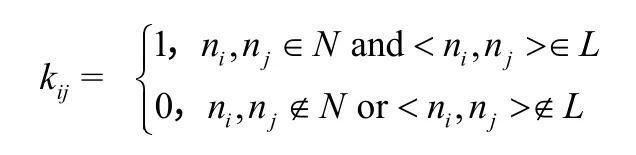
矩阵 2:路网交通状态邻接矩阵M={mij},此矩阵在路口邻接矩阵的基础上,加入时变的路段交通状态信息,包括路网交通参数等信息:
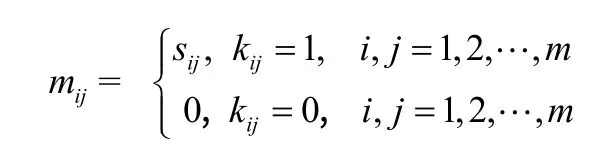
矩阵 3:路网交通状态连通矩阵C={cij(λr)},此矩阵表示在给定路网拥挤截值 λr下路网连通状态,包括路网交通参数信息以及交通状态判定信息:

矩阵4:路网交通状态可达矩阵T={tij(λr)},此矩阵表示在给定路网拥挤截值 λr下路网可达关系:路网交通状态可达矩阵由路网交通状态连通矩阵进行两类布尔运算(逻辑乘,逻辑加)得到:T=Cn+1,n 其元素值为{0,1},n 为运算次数。当路口 ni与 nj之间至少存在一条通路且各路段交通状态系数小于路网拥挤截值时,值为1,否则为0。
路网次分层方法如下:
步骤1:计算在当前路网交通状态可达矩阵中路口 ni能到达的路口集合,记为

能到达路口 ni的集合,记为
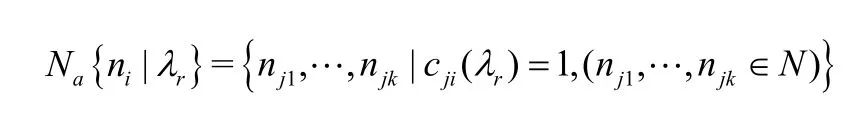
步骤2:考查与路口 ni相连通的路口,判断与路口 ni互通的路口集合与路口能到达的路口集合是否相等,即判断
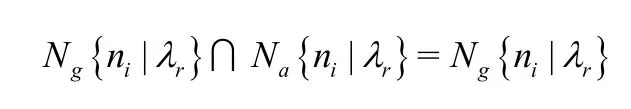
是否成立,若成立,则 Ng{ni|λr}中的路口放入路网次分层的最上层。
步骤3:在路网可达矩阵中划去步骤2 中确定的上层路口,若所有路口均划入所属层次中,计算结束。否则,在新的路网可达矩阵中,回到步骤1继续计算。
次分层产生的各层路口中,处于最上层的路口可达性好,即到达该路口的道路畅通,从该路口到达其他路口拥挤。处于最下层的路口可达性差,即从该路口到达其他路口畅通,其他路口到达路口道路拥挤。处于中间层的路口能够到达其他路口,其他路口也可以到达该路口。
2 基于路网二次分层的出行诱导路径优化方法
Dijkstra 算法是一种典型的单起始点的最短路径算法,通过树形结构来寻找最短路径,算法的时间复杂度为O(n2);A*算法是在Dijkstra 算法基础上的进一步改进,通过从起始点进行前向搜索且从目标点进行后向搜索来计算最优路径,算法的时间复杂度为 O(bc)。与平面算法相比较,分层算法的时间复杂度从O(d4)下降到 O(logad)。其中,n 为路网中节点个数;b 为道路节点长度,一般不超过4;d为路径长度;a 为与道路分层标准有关的常量。
鉴于以上分析,论文在路网二次分层模型基础上,采用限制区域的 A*算法寻找最短路径,进行最优出行路径的“三段寻径”过程,具体计算步骤如下:
步骤1:对路网进行初分层,形成的各层路网分别为子网0,子网1,子网2,…,各层子网内的道路等级高低由子网0 依次递减,子网数量原则上不大于3。
步骤2:判断起点S 与终点D 所在的子网是否为子网0,如果不是,分别寻找与起点及终点最近的子网0 上的节点 S' 以及 D'。
步骤3:以起点S 与终点D 之间的路网为出行路径搜索区域,去除不必要的道路数据。
步骤4:进行出行路径的“三段寻径”,巡径路段共分三段:寻找起点S 到高层次路网较近节点S '之间的最优路径route(S→S'),寻找高层次路网较近节点 D '到终点D 之间的最优路径route(D'→D),寻找 S '到 D '之间的最优路径route(S'→D')。
步骤5:每段寻径过程均采用限制区域的双向A*算法,得到初始优化路径。
步骤6:引入交通状态阈值,分别对S→S',S'→D',D'→D之间的路网进行次分层,判断初始优化路径中各个路段的可达性。
步骤7:将路径中不可达路段的两端节点降入低一级子网,在低一级子网重新进行路径搜索,直至优化路径中所有路段均符合路段可达性标准,算法结束。
图2 为最优出行诱导路径搜索示意。

图2 最优出行诱导路径搜索示意Fig.2 Searching chart of the optimal travel route
3 示例应用及分析
以图3 中的路网布局为例,进行出行路径诱导选择的实例分析:出行者驾车从图中S 点出发,停车地点为D 点。
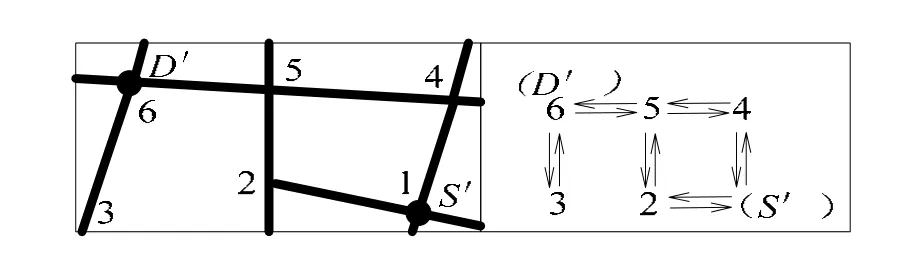
图3 S' 与 D' 之间路网拓扑Fig.3 Topological graph of the road between S' and D'
在路网初分层时将路网分成两个层次:①子网0 层为路网等级较高层,主要包括快速路、主干路以及通过性好的次干路;②子网1 层为路网等级较低层,主要包括可达性好的次干路以及支路。分层结果如图4 所示。
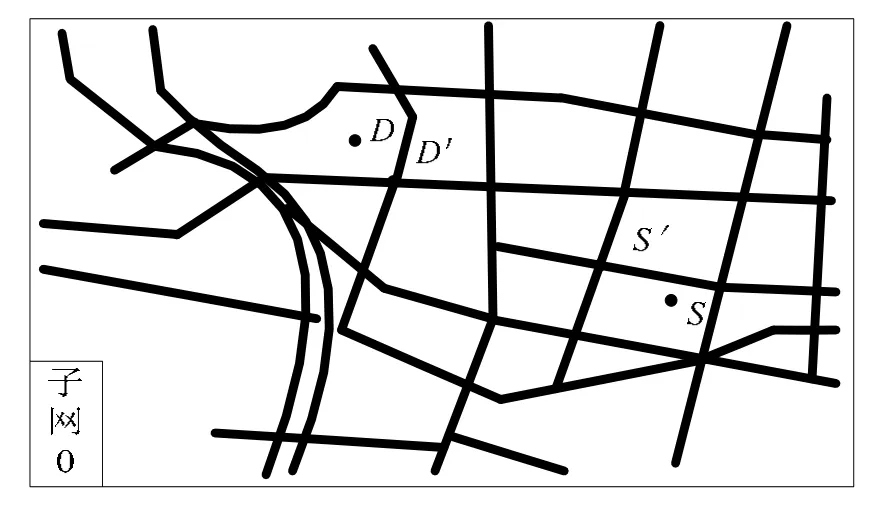
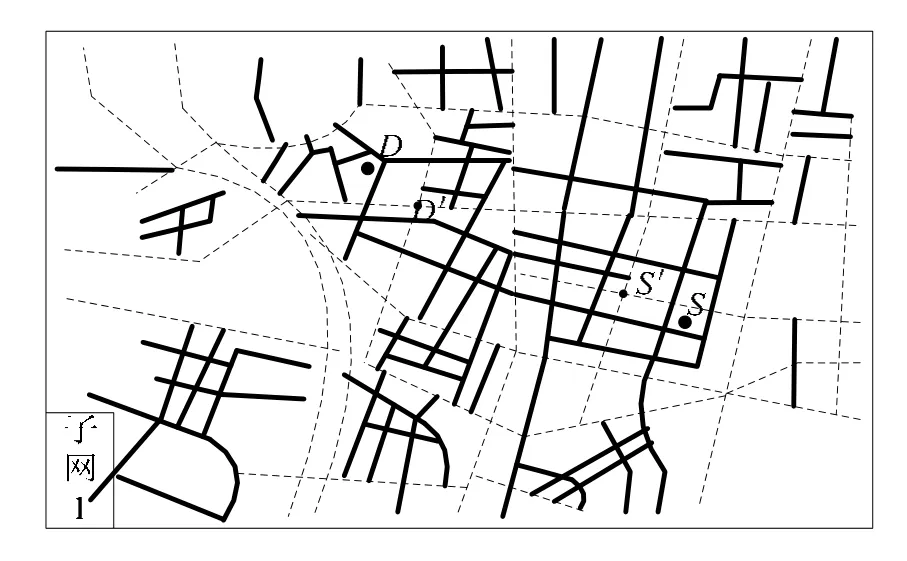
图4 路网初分层Fig.4 Initial Hierarchy of the road network
按照S→D 的路径搜索方向,在子网0 上寻找节点 S' 以及 D',利用限制区域的双向A*算法,在子网1 搜寻路径:
route(S→S'),route(D'→D),在子网0 搜寻路径:route(S'→D');
由于篇幅限制,下面以搜寻route(S'→D')为例,对算法进行具体说明:
利用 S' 与 D' 之间的矩形区域缩小路网的搜索范围,路网拓扑结构图以及各路段参数如图3 与表2 所示。

表2 矩形搜索区域内各路段交通参数Tab.2 Road parameters of the rectangle searching district
在矩形搜索区域内,利用 A*搜索算法很容易计算出route(S'→D')=①-②-⑤-⑥
下面在子网0 层,对 S' 与 D' 之间的路网进行次分层,计算相关矩阵,并判断路网中各节点间的可达性。
计算路口邻接矩阵如下:

计算路网交通状态邻接矩阵如下:

通过表2 可知路段上车辆的平均行程速度介于20km/h~30km/h,属于轻微拥堵。选择路网拥挤截值λr=0.05,计算路网交通状态连通矩阵以及路网交通可达矩阵如下:

表3 为路网次分层迭代计算。
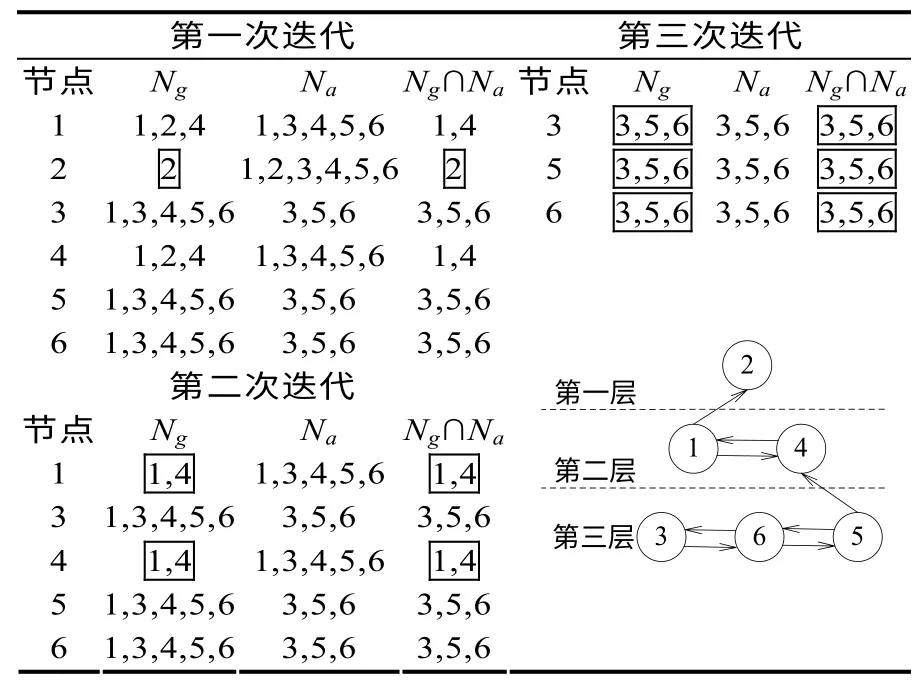
表3 路网次分层迭代计算表Tab.3 Calculating table of the second hierarchy of the road net
S′到D′初始优化路径为①-②-⑤-⑥,表3 中次分层结果显示:节点②处于最上层的路口,可达性好;节点⑤处于最下层的路口,可达性差。因此,由节点②驶往节点⑤的可达性差,需要在低一等级的路网——子网1 中搜索②→⑤的最优路径,同样,用A*算法很容易子网1 中得到②→⑤的优化路径,并用同样的方法进行路网次分层分析②→⑤的优化路径上节点之间的可达性,得到route②→⑤。(表3 中,每次迭代过程中Ng与Ng∩Na数值时,用方框标注以示区别)
以上巡径过程对于route(S→S')以 及route(D'→D)同样也适用。最终S 到D 的最优出行诱导路径为:
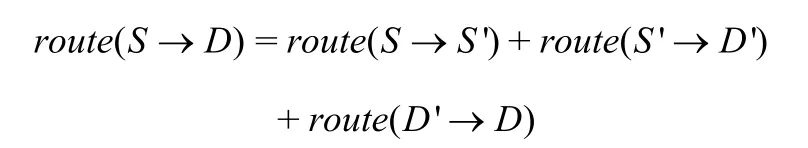
如图5 所示。
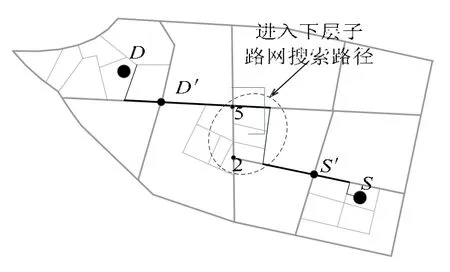
图5 最优路径搜寻结果Fig.5 Result of the optimal travel route
4 结束语
平面算法是求解最短出行路径的传统方法,但是其效率会随着路网规模的扩大、节点数的增加而急剧下降。论文采用基于路网二次分层的出行诱导路径优化算法,通过对道路网进行分层抽象,再选择合适的路网层进行搜索,由于其本质上大幅度缩减路网的规模,解决了大规模路网路径搜索效率低的问题。
算法在宏观方面考虑了路网的结构(等级结构、功能结构、布局结构),在微观方面考虑路网运行的交通参数(平均行程时间、平均行程速度、路段拥挤状况),拥挤状态阈值的选取与交通流状态保持一致,达到在畅通状态下,满足出行者使用高等级道路出行的倾向(此时,大部分路段的交通状态系数都小于拥挤状态阈值,高等级路网不存在不可达节点,不用下降到低等级路网搜寻路径);在拥挤状态下,调节拥挤的高等级路段上交通流的作用(此时,拥挤路段的交通状态系数大于拥挤状态阈值,部分节点间路径下降到低等级路网进行搜寻,优化的出行路径将减轻高等级道路上的交通压力)。因此,该算法搜索效率高、搜索结果优,可以较好的应用于出行诱导、交通控制等系统中。
[1]Zhan F.B.,Noon C.E.Shortestpath algorithms:An evaluation using real road networks[J].Transportation,1998,32(1):65-73.
[2]Huang B.,Wu Q.,Zhan F.B.A Shortest path algorithm with novel heuristics for dynamic transportation net-works[J].International Journal of Geographical Information Science,2007,21(6):625-644.
[3]Goldgerg A.V.,Kaplan H.,Werneck R.F.Reach forA*:Efficient point-to-point shortest path algorithms[A].Proceedings of the 8thWorkshop on Algorithm Engineering and Experiment Vancouver SIAM,2006.
[4]Sanders P,Schulters D.Engineering highway hierarchies[A].Proceedings of the 14thAnnual European Symposium on Algorithms Berlin:Springer,2006:804-816.
[5]王海梅,周献中.一种限制搜索区域的最短路径改进算法[J].南京理工大学学报,2009,33(5):638-642.
[6]吴成东,韩中华,张颖等.基于并行遗传神经网络算法的限制搜索区域最优路径方法[J].公路交通科技,2006,23(8):126-142.
[7]王亚文,汪西莉,曹 菡.一种限制搜索区域的多比例尺最优路径规划算法[J].计算机应用研究,2007,24(12):66-71.
[8]Jagadeesh G.R.,Srikanthan T.,Quek K.H.Heuristic techniques for accelerating hierarchical routing on road networks[J].IEEE Transactions on Intelligent Transportation System,2002,3(4):301-309.
