基于改进克隆算法的WSN 的QoS 路由研究
2013-10-21肖刚,谢红
肖 刚,谢 红
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
无线传感器网络(Wireless Sensor Network,WSN)是一种由大量随机分布的微小传感器节点,以自组织的方式构成的大规模、无人值守、能量受限的分布式网络,其传感节点包含传感器、数据处理单元和通信模块.无线传感网络具有广阔的应用前景,但其自身也存在着环境等约束问题,并且其在通信交互过程中传输、路由等也受到各种约束[1].因此,只有综合考虑平衡各种约束才能客观解决实际问题,才能最优地选择更适合的传感器节点,保证在最优路径选择基础上,节约了通信成本.提高服务质量(QoS)成了WSN 设计中的一个主要问题.在WSN 中,QoS 路由的目的就是在网络中寻找满足系统对路径的带宽、时延、丢包率、费用要求的路由,而基于多个不相关可加度量的QoS 路由问题是NP 完全问题.
本文在克隆选择算法和蚁群算法融合的基础上,提出了一种克隆蚁群算法,克隆选择算法在搜索的初期具有较高向最优解收敛的速度,可以快速对解空间全局搜索,将更优秀的解保存在记忆库,更快地引导蚁群系统找到全局最优解.但伴随着搜索的持续进行,由于针对系统中的反馈信息利用不足会导致大量无用的冗余迭代,使求最优解的效率显著降低[2].而蚁群算法在搜索的初期受限于信息素的缺乏,使得搜索速度相对缓慢,只有当积累信息素到一定的强度后,通过信息素的累积和更新收敛最优路径解,将最优解的收敛的速度显著提高.本文将该算法应用于QoS 路由研究中,仿真结果表明,克隆蚁群算法的求解性能要明显优于常规的蚁群算法.
1 克隆选择算法原理
克隆选择算法是一种由无性繁殖过程中生物获得免疫进化来的优化算法,当免疫细胞持续产生基因突变,细胞的多样性得到了极大丰富.当生物体内免疫细胞的多样性到达了某种程度后,每种抗原入侵机体都能被机体识别,并且机体能可以克隆出相应的免疫细胞并激活,分化和增殖,进行免疫应答,进而最后消灭抗原.克隆算法分别在抗体种群和优秀抗体记忆集中实现克隆选择操作,全面地模拟了生物免疫系统克隆选择的过程,更好地保持了抗体种群的多样性[3].算法描述如下:
1)抗体初始化:首先确定抗原,然后随机产生若干个抗体,Ad为抗体集合,其由临时抗体集Ad{r}和记忆抗体集Ad{m}两个集合组成.
2)抗体亲合力计算:计算Ad 中每个抗体的亲合力.
3)抗体选择:从Ad 中连续选择n个亲和力最高的抗体,生成临时抗体集Ad{r}.
4)抗体克隆:分别对已选择的n个抗体进行克隆复制,按照抗体亲合力高低,成一定比例进行抗体的克隆复制.
5)抗体变异:对克隆后的抗体集进行变异操作.
6)抗体选择:再次计算变异后的新抗体集的亲合力,评估变异后的抗体[4-5],如果抗体亲合力优于Ad{r}中抗体的亲合力,则用新抗体替换原抗体,产生记忆抗体集Ad{m}.
7)抗体记忆:利用m个新产生的抗体替换Ad中亲合力较低的m个抗体,保护了抗体的多样性.
8)判断是否达到进化条件:评估是否达到进化条件,如不达标,转2),执行下一轮进化,否则,转9).
9)抗体解码,输出问题的解.
2 蚁群算法原理
蚁群算法是一种应用于组合优化问题的启发式仿生优化算法,蚂蚁在觅食的活动中,可以在其途径的路径上留下信息素,并且蚂蚁是通过路径上的信息素强度来决定选择该路径的概率.路径上的信息素是根据选择这条路径蚂蚁的多少来按比例增加的,信息素强的路径被后继蚂蚁选择的概率也高,进而该路径的信息素强度持续增强.信息素越强会吸引越多的蚂蚁,这种自发的集体行为产生了一种信息正反馈机制.在此机制下,蚂蚁可以找到巢穴和食物源之间的最短路径.
蚁群算法的优点是良好的分布式计算机制,灵敏的正反馈性,较强的稳健性,易于与其他算法融合等特点.不过蚁群算法因为易早熟,初始搜索比较盲目,运算时间较长等缺点,造成了其使用范围受限.为了更好的解决这些缺点,很多学者针对不同切入点和情况,将蚁群算法和其他算法结合,创造出了性能更优越的复合算法,改进信息素更新策略,制定选择策略,加入其他算法算子等方式,都是目前主要对蚁群算法改进的方向.
3 WSN 网络QoS 组播路由模型
QoS 路由问题是在满足一个或多个QoS 条件基础上,寻找传播路径的问题,可以将其抽象成求最小值的数学模型.Steiner 树是一棵连接所有节点的总代价最小的分布树,它使连接特定图中的特定组成员所需的链路数最少.已知求解Steiner 树是一种P=NP 的NPC 问题,但因为在实际的无线传感器网络中存在各种限制条件,所以高复杂度算法不适用于求解WSN 中的QoS 问题,故采用启发式算法求解Steiner 树.
在无线传感器网络中,一般从以下两方面考虑QoS 组播路由:业务方面和网络能耗.其中业务方面需要满足业务提出的带宽,延迟、时延抖动,丢包率等QoS 要求;而网络能耗方面为了能延长网络节点使用寿命.
网络模型可以表示成赋权图G(V,E),式中V是图中所有网络节点的集合,E 是网络双向路径的集合[6],每一条边代表每2个节点之间的通信路径,假设网络是对称的.T(s,M)表示组播树,其中s∈V为源点,M∈{V-{s}}为终点.
组播树T(s,M)中,存在下列关系:
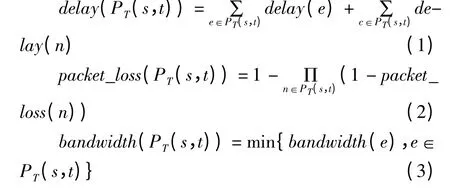
其中:PT(s,t)是组播树T(s,M)上源点s和终点t 间的路由[7].


其中:DL、BW、PL 分别为业务对网络时延、带宽、和包丢失率的约束限制.在多数现实情况中,时延和包丢失率是最需要优先考虑的,故本文只综合考虑时延和包丢失率,带宽等约束.
4 克隆蚁群算法设计
4.1 克隆选择算法关键部分
4.1.1 初始抗体的生成和新群体的产生
对网络拓扑结构进行精简处理,本文中通过删除不满足指定带宽约束的链路,将网络精简成新的,高效的网络,若源点s和终点t 处于同一连通分量,即把此连通分量作为算法研究的基图[8].以下的研究将忽略带宽约束,只考虑延迟、丢包率和费用度量.
4.1.2 抗体的评价
抗体与抗原间的亲和度作为抗体的优劣是判断依据,其亲和度定义为:

其中:A,B,C 分别为fpl,fbw,fdl的加权系数,分别表示包丢失率、带宽和延时在目标函数中所占的比重.其值根据系统情况具体设置,在本系统中,由于更侧重信息的安全性,分别设置A=1,B=0.8,C=0.8,Θpl,Θbw,Θdl是包丢失率,带宽,时延的惩罚函数,当满足各自约束条件时值为1,否则为0.5.
4.1.3 克隆,交叉,变异
依据式(8)计算出全部个体的亲和度,从中选择n个亲和度最高的个体;克隆规模根据亲和度高低按正比比例复制选出的个体,形成一个临时种群C.对于临时种群C,首先执行概率的交叉操作,为了避免产生不合理路径,本文采用单点交叉方法.从群体中随机选择两条路径,从中随机选择两个节点a、b,交换a,b 之间的部分,然后删除路径中重复部分.然后对其进行高频变异,随机选取一个路径,在该路径中随机找一个节点k,然后以k为起点,以原目的节点为终点,随机搜索一条不含k 之前所有节点的节点取代k.获得一个变异后的抗体群C .记忆单元M 由改进的克隆个体组成,并添加到候选解集中,作为新一代候选解集P.依据更新概率,最后随机产生了一些新的抗体替换d个亲合度低的旧抗体,保证了抗体的多样性.
4.1.4 结束条件
判断是否达到循环终止条件.将亲和度的最大阈值或最大允许的迭代次数设为循环终止条件[9].如果满足,将当前的记忆集保存,结束循环.否则,转第3 步.
4.2 蚁群算法关键部分
4.2.1 路径的选择
假设蚂蚁k 由当前城市i 选择下一个要走的节点j,则所依据的概率转换规则为:
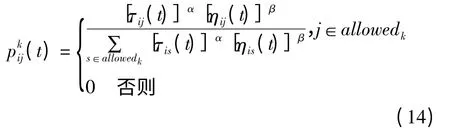
其中:α 表示第k 只蚂蚁在运动过程中积累的信息素浓度,β 表示启发因子在蚂蚁选择路径中的重要程度,allowedk包含着蚂蚁k 下一步允许转移的节点子集,ηij(t)代表搜索路径中的启发信息,τij(t)表示在t 时刻链路(i,j)上的信息素量.
4.2.2 局部信息素的更新规则
为避免信息素残留导致启发信息被淹没,当蚂蚁成功完成路径选择后,要对路径上的信息素按如下公式进行局部更新:
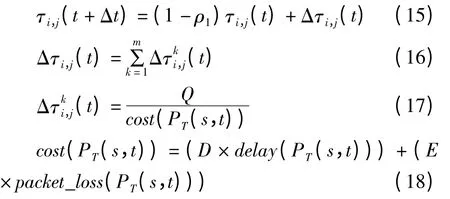
其中:0 <p1<1,表示信息素挥发系数,cost(PT(s,t))为第k 只蚂蚁在一次循环中所花费的总费用,由于在程序中对带宽进行了约束处理,所以cost(PT(s,t))并不包含fbw.D,E 是时延和丢包率的加权系数,考虑到丢包率在实际系统中的值比较小,通过控制加权系数使时延和丢包率维持相对平衡,在本系统中,D=0.5,E=100.Q 是常量,用于调整信息素强度.当没有局部更新时,蚂蚁将在上一次选择的最佳路径的相邻区域内搜索.
5 仿真实验及结果
实验仿真如图1所示.仿真过程中,网络拓扑模型是建立在20 km×20 km 的正方形区域内,由基于C-均值聚类的随机网络拓扑生成器随机在该区域内随机生成50个节点,其链路带宽在[1,20]之间、节点能量在[1,20]之间随机产生,其中时延的取值为两节点间的距离除以2/3 光速,单位为ms,带宽单位为MB/s.通过多次试验,选出拓扑图最好的作为研究环境[10-11],见图1,各个边的特性用三元组(b,d,r)描述,其中b、d、r 分别表示带宽、延时和丢包率.同时,选出源节点S=1和目的节点集Des=[6 9 10 15 20 24 31 36 42 48].
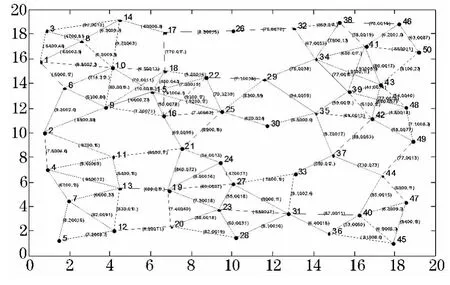
图1 仿真使用的网络拓扑模型
通过把CSACO(克隆蚁群算法)与ACO(蚁群算法)仿真结果进行对比,评价费用和端到端时延这两个性能指标参数.如图2所示,可见总费用随着迭代次数增加,CSACO 与ACO 的费用都有所下降,但CSACO 要稍好,这是因为CSACO 在数据传输时,在保证丢包率和时延基础上,可以极大程度选择更好的路径进行传输,提高了成功率.
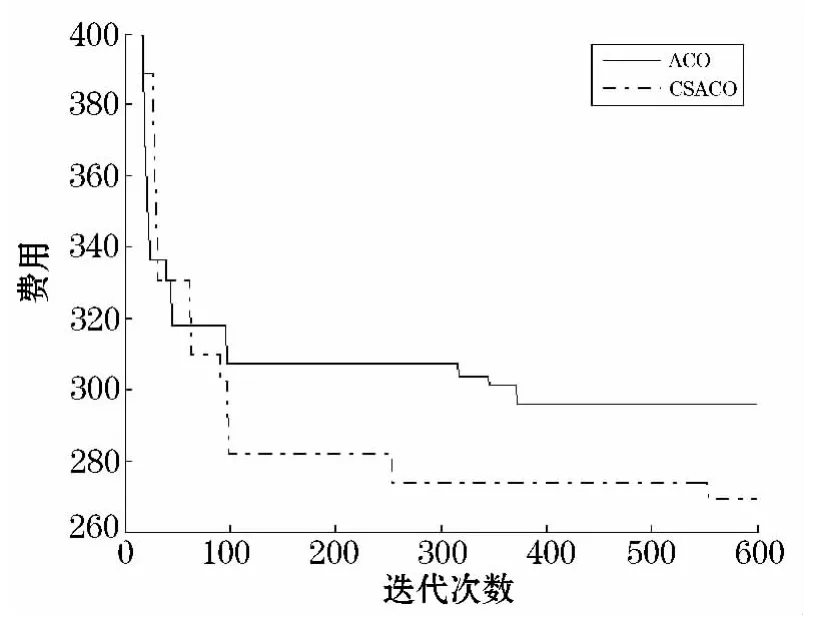
图2 CSACO 与ACO 总费用比较图
如图3所示,时延随着迭代次数的变化情况逐步下降.其中CSACO 算法比ACO 算法在时延方面表现出更好的性能.这是因为CSACO 将时延作为QoS 约束条件之一,所以会在选择路由过程中挑选时延参数更合理的路径.

图3 端对端时延比较图
由图2、3 可以看出,随着迭代次数的增加,时延和费用的变化不是递减的,而费用值是逐渐减小的,直到收敛于恒定值,符合QoS 多约束的规律.
表1 中,Max 代表运行50 次实验最小费用Cost 的最大值,Min 代表最小值,Average 代表平均值,Var 代表方差,Diedai 代表找到最小费用Cost的平均迭代次数,Time 代表运行50 次的总时间.从表1 中的数据可以看出,CSACO 算法得到最小费用Cost 的平均值、平均迭代次数和方差都比较小,故性能稳定.
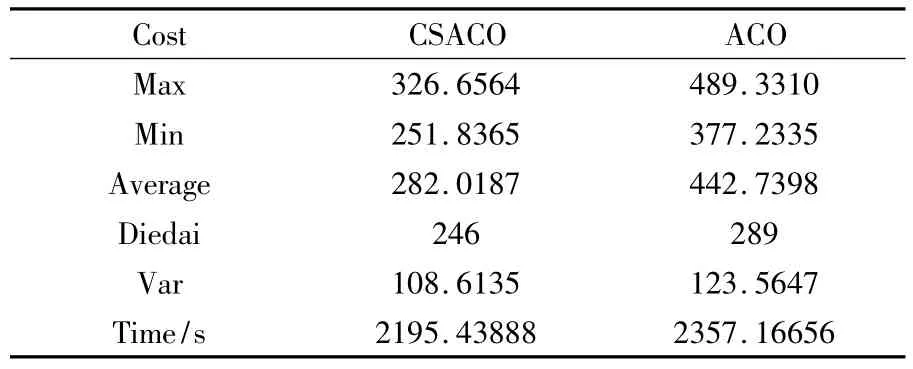
表1 50 次实验,算法平均指标比较
6 结语
针对WSN 网络QoS 组播路由问题,提出了一种基于改进克隆算法的QoS 组播路由算法.本算法在蚁群算法基础上融合了克隆选择算法的快速随机的全局搜索能力,解决了常规蚁群算法的收敛速度慢、易过早局部最优等缺点.仿真结果表明,CSACO 算法提高了路由搜索速度,在保证最优路径选择基础上,节约了通信成本.
[1]于海斌,曾 鹏,梁 韦.智能无线传感器网络系统[M].北京:科学出版社,2006:30-40.
[2]肖 伟,全惠云,刘 枫.基于蚁群算法的多路径多约束QoS路由的研究[J].计算机工程与应用,2008,30(7):89-94.
[3]焦李成.多目标优化免疫算法、理论和应用[M].北京:科学出版社,2010:150-184.
[4]毕晓君.信息智能处理技术[M].北京:电子工业出版社,2010:310-314.
[5][南非]ENGELBRECHT A P,著.计算群体智能基础[M].谭营,译.北京:清华大学出版社,2009:344-356.
[6]胡 细.移动自组织网络中若干问题的建模与分析[D].上海:上海大学,2007.
[7]孙利民,李建中,陈 渝,等.无线传感器网络[M].北京:清华大学出版社,2005:248-254.
[8]SALAMA H F.Multicast routing for real-time communication of high-speed networks[D].Raleigh:North Carolina State University,2006:28-37.
[9][美]STALLINGS W.无线通信与网络[M].何 军,译.北京:电子工业出版社,2006:267-278.
[10]蔡 慧,刘洪波.基于K 均值聚类的随机网络拓扑模型[J].计算机工程与设计,2009,30(5):1089-1901.
[11]那成亮,周廷显,芦东昕.基于博弈的无线传感网络功控算法收敛性分析[J].哈尔滨商业大学学报:自然科学版,2007,23(1):92-95.
