基于MATLAB的大型储罐完整性评价系统的开发

郭菲菲，王北福，聂立宏，王东杰

(浙江海洋学院石化与能源工程学院，浙江舟山 316004)

随着我国国家石油储备战略基地的建设，大型储罐所潜藏的环境污染以及所引发的着火爆炸事件更加严重，使安全、环保和长周期运行的风险随之大幅度增加，对大型储罐的运行和安全管理工作也提出了更高的要求。采取有效措施，避免和减少大型储罐的安全事故，变预防性的周期检修模式为以风险管理为核心的完整性管理模式，是管理者面临的重大问题[1]。目前，国外已经开发了多种风险评价通用性评价软件，如SAFETI，SAVE II，SIGEM，WHAZAN等，但是这些软件都不是针对大型储罐而开发的[2]。由于国外通用性软件针对性不强、操作复杂、价格昂贵，因此开发专门针对大型储罐的完整性评价系统具有很大的社会经济价值。

1 软件开发的理论模型

储罐底板的损坏形式有很多种，如底板腐蚀、底板凹陷、罐底表面由于受到外力后留下的硬伤等等。储罐在储存过程中，底板上表面直接接触含杂质的污水或沉淀水，使之工作状况不理想，从而加速了底板表面的腐蚀。

对于储罐来说，其腐蚀深度是在逐步增加的，那么它的可靠性也是逐步变化的。而储罐腐蚀底板的可靠性计算可以以两种方式存在：一种是根据实测数据进行可靠性计算，即静态可靠性计算；另外一种是根据实测数据进行可靠性预测计算，即动态可靠性计算。在实际应用中，还有一种情况就是：需要知道在给定可靠度的前提下知道剩余使用寿命，即计算可靠寿命[3]。下面将对这三种方式进行建模。

1.1 静态可靠性模型

根据大量的实验数据和理论模型，大型储罐局部最大腐蚀坑深度服从Gumbel第一类渐近分布函数（即极值Ⅰ型最大值分布）[4]，累积分布函数和概率密度函数分别如下：

其中，x/mm为最深腐蚀孔深度的随机变量；r/mm为数据分布的位置参数；a/mm为数据分布的尺度参数。

极值Ⅰ型最大值分布中随机变量的数学期望和方差为：

大型储罐使用t年之后，从底板上选择n块腐蚀较为严重的区域，测得一组最大腐蚀深度数据为x1，x2，…，xn，则在t年内的腐蚀深度均值及标准差分别为：

那么大型储罐底板的可靠性，可用下式计算：

式中，xmax为最大许可腐蚀深度。

1.2 动态可靠性模型

对于大型储罐动态可靠性的计算，就必须引用腐蚀速率v，假设腐蚀速率和腐蚀深度成线性关系[5]，即：

根据统计学原理，再引入腐蚀深度的变异系数，即：

由（8）、（9）两式可知，使用t0年后继续使用t1年的腐蚀深度均值和标准差分别为：

引入腐蚀速率v和腐蚀深度的变异系数Bx，把大型储罐腐蚀动态问题转化为静态问题，则可按照静态模型进行计算。

1.3 可靠寿命模型

当已知大型储罐腐蚀底板的可靠度R(tr)=p(t＞tr)=R0，便可求解当可靠度为R0时的可靠寿命：tr:tr=R-1(t)

对于腐蚀寿命来说，它服从的分布是极值Ⅰ型最小值分布[6]。其累积分布函数和概率密度函数分别如下：

其中，t/a为腐蚀寿命；rt/mm为数据分布的位置参数；at/mm为数据分布的尺度参数。

极值Ⅰ型最小值分布中随机变量的数学期望和方差为：

储罐底板的腐蚀寿命均值和标准差分别为：

那么得到实测数据之后，储罐腐蚀底板的可靠度为：

则储罐腐蚀底板的可靠寿命tr为：

则剩余寿命为

2 大型储罐可靠性模型求解

可靠性模型的求解关键在于对分布函数的参数进行估计。参数估计方法主要有图解法、矩法、最小二乘法、最大似然法和区间估计。本模型使用的是矩法，则根据矩法公式：

然后分别代入极值Ⅰ型最大值和最小值分布中随机变量的数学期望和方差，可以分别得出极值Ⅰ型最大值和极值Ⅰ型最小值分布函数的参数如下：

通过求得分布参数r，a，rt，at，可对大型储罐腐蚀底板的静态可靠度、动态可靠度以及可靠性寿命进行评估。

3 基于MATLAB的软件的开发

某油库的储罐已经工作47 a，储罐底板原始厚度为4 mm，xmax取2 mm[7]。根据油库储罐底板腐蚀分布区域性强的特点，选取正对采光孔1，采光孔2，呼吸阀，量油孔，U型压力计的底板区域，选取的面积均为100 cm×100 cm。测得这5个区域腐蚀深度的最大值数据，见表1。

表1 实测腐蚀深度数据（mm）Tab.1 Measured corrosion depth data(mm)

将实测腐蚀深度数据保存到access数据库中，再根据上述几种对储罐可靠性数学模型，运用MATLAB编程分别对静态可靠性模型、动态可靠性模型和可靠寿命模型进行计算，运行结果如图1、2所示。

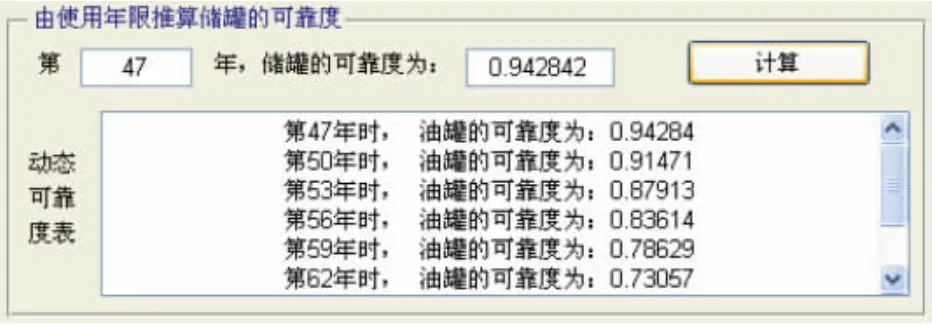
图1 储罐的动态可靠度运行结果Fig.1 Running results of dynamic reliability of tank

图2 储罐的动态可靠寿命运行结果Fig.2 Running results of dynamic reliable life of tank

4 结论

本文建立了大型储罐可靠寿命预测模型，利用对分布函数的参数进行估计来对模型进行求解，通过对某油库一个47 a储罐评估，表明该方法预测数据与实际运行状况较接近，适合于工程应用，能够解决大型储罐管理中遇到的实际问题。

[1]王 光,李光海,贾国栋.常压储罐群的完整性评价技术[J].压力容器,2009,26(7):29-32.

[2]American Petroleum Institute.API PUBL 35322006 Managing Systems Integrity of Terminal and Tank Facilities/Managing the Risk of Liquid Petroleum Releases[S].Washington:API Publishing Services,2006.

[3]肖 杰,刘丽川,欧益宏.油罐底板腐蚀的可靠性计算研究[J].腐蚀与保护,2005,26(5):205-207.

[4]曹楚南.腐蚀试验数据的统计分析[M].北京:化学工业出版社,1988.

[5]喻天翔,张祖明.印刷机滚筒的耐腐蚀可靠性设计[J].北京印刷学院学报,2002,10(4):12-14.

[6]戴树和.可靠性工程及其在化工设备中的应用[M].北京:化学工业出版社,1986.

[7]杨定中,刘恩林.一种白色防水隔热弹性涂料[P].CN1250073A,1999.