基于误差修正的BP神经网络含沙量预报模型

2013-10-20黄清烜梁忠民曹炎煦霍世青许珂艳

水力发电 2013年1期

黄清烜，梁忠民，曹炎煦，霍世青，许珂艳

（1.河海大学水文水资源学院，江苏南京 210098；2.黄河水利委员会水文局，河南郑州 450004）

0 引言

黄河是世界上输沙量最大、含沙量最高的河流之一。开展含沙量过程预报，不仅是黄河中下游干流水库调度和洪水资源化的需要，也是下游变动河床水位预报的需要[1]。目前，含沙量预报的方法中，水文-水动力学方法主要包括输沙单位线模型、响应函数模型、1-D～3D水沙数学模型等[2-7]。该类方法往往需要输入大量的水文、气象、河道特性、工程布局等资料且计算时间较长，因而限制了其应用范围；基于宏观因果关系的系统分析方法[8-11]，如神经网络模型、支持向量机模型等对资料要求相对较低，在含沙量预报的实际应用中发挥着一定作用。

BP网络模型在水文预报领域应用广泛[12-14]。本文在借鉴已有BP网络模型研究成果基础上，建立了考虑上游来沙及区间降水的含沙量BP网络预报模型，并将其应用于潼关站含沙量过程的预报；同时，结合误差自回归模型对BP网络的预报结果进行校正，并对比分析了校正前后预报结果的精度，为实际应用提供参考。

1 BP网络模型

BP（Back Propagation）网络是一种按误差逆传播算法训练的多层前馈网络。标准的BP神经网络收敛速度慢，易陷入局部最小点，对神经元个数比较敏感[12]。为此，众多学者提出了各种改进方法[12-13]。动量-学习率自适应调整算法就是其中一种典型的改进方法。该方法可以有效地降低网络对于误差曲面局部细节的敏感性，提高收敛速度，并抑制网络陷于局部极小值。其改进算法如下

其中α为动量因子，0≤α＜1。学习率自适应调整法使学习率随网络训练发生变化，在训练开始阶段学习率要取大些，有利于提高网络的训练速度；在训练后期，学习率取小些，以保证网络收敛在误差最小点。该方法的实质就是在每个权重调整量上加上一项正比于前一项权重的值。

2 误差自回归实时校正模型

实时校正就是利用在作业预报过程中不断得到的预报误差信息，运用现代系统理论及时地校正、改善预报估计值或水文预报模型中的参数，尽可能地减小以后阶段的预报误差，使预报结果更接近实测值。根据与预报模型的结合方式，实时校正方法可分为预报与校正模型耦合及预报加校正模型两类。其中，误差自回归实时校正模型简单、实用。

误差自回归实时校正模型的工作原理:首先，采用确定性预报模型进行预报；之后，利用预报值与实测值之间随时间变化的误差序列建立误差自回归模型，预报未来误差；最后，再将预报值与预报误差值相加得出校正后的预报值。误差自回归估计的表达式可写为

令k=0，1，2，…，n－1；并考虑 ρk=ρ－k和ρ0=1，可得到 n阶线性方程组。即Yule-Walker方程

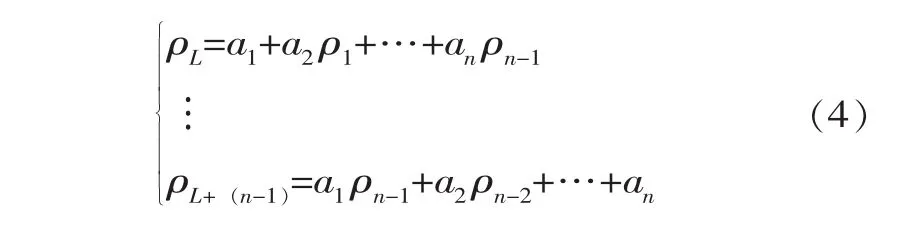
在实际应用中，通常采用样本自相关函数r代替总体ρ来估计参数a，则式（3）可写为[15]

其中，rk可以通过实际水文过程的离散点数据资料由

求得模型参数；a可用递推公式求解，即由自回归模型中已知的低阶参数递推求得高阶参数。设a（i，j）表示i阶自回归模型中第j个参数，则递推公式可写为

通过式（7）可求出自回归系数 a1，a2，…，an，进而求得 a0=u（1－（a1+a2+…+an））。其中， u为误差序列的期望，可以用样本均值代替。

3 实例

3.1 流域基本资料

黄河中游龙门—潼关的河段干流河道长132.6 km，因其游荡性的河道特性有别于晋陕峡谷河道（大北干流）而称为小北干流，区间汇入的支流有汾河、涑水河、北洛河、渭河、泾河（在高陵县汇入渭河），其中渭河、汾河是黄河最大的两条支流[16]。该河段为堆积性河段，河段比降上陡下缓，河床宽浅，水流散乱多边，河心洲浅滩密布。该河段洪水多出现在汛期7月～10月，具有上涨快、历时短、流量变幅大、含沙量高等特点。 “揭河底”是该段河流特殊的水文现象。

3.2 BP网络预报模型的建立

潼关站的含沙量由其上游各支流的来沙及流域内降雨冲刷泥沙共同组成。按文献[5]所提供的方法，选择上游各控制站的含沙量Qsi（t－τi）和流域48 h的累积面平均雨量（t－υ）作为模型的输入因子。其中，i为控制站的数目；τ为控制站到潼关的沙峰传播时间；υ为累积面平均雨量对潼关站含沙量的影响滞时。在资料的收集过程中，发现北洛河和涑水河径流量很小并经常出现断流，直接导致状头站和张留庄站缺少含沙量的实测资料。为此，最终采用龙门、河津、华县作为上游来沙的控制站。统计分析1980年～2005年的历史洪水资料（时段为1 h），确定龙门、河津、华县到潼关的沙峰传播时间τ分别为25、22、20 h，48 h累积面平均降雨量对潼关含沙量的影响滞时υ为20 h。分析最终确定， Qs龙（t－25）、Qs河（t－22）、Qs华（t－20）、（t－20）作为模型的输入变量，Qs潼（t）作为模型的输出变量。通过试算选取隐含层节点数为6，建立网络拓扑为4-6-1，传递函数为Sigmoid函数的三层BP神经网络模型。

在实际的网络训练过程中，考虑到以Sigmoid函数为传递函数的BP神经网络的输出值域均在[0，1]之间，并为消除因含沙量和降雨量量纲的不同对网络识别精度的影响，需对输入变量进行归一化处理。本文用最大最小法进行数据的归一化处理，计算公式如下:

式中，xi、x′i分别为输入变量归一化前、后的输入变量； xmin、xmax分别为输入变量中的最小值和最大值；N表示训练样本的总个数。

3.3 实时校正模型的建立

通过样本的训练，确定BP网络模型的权重及阈值，并基于该权重及阈值获得潼关站的泥沙模拟结果。分析比较实测值与模拟值系列，求得误差序列，并通过该误差系列，建立误差自回归模型。设潼关站实测含沙量序列为｝，预报含沙量序列为｝，则误差序列可表示为 e（i）=。根据 AIC 准则法确定模型阶数为5，建立预见期为6 h的误差自回归模型，表达式可写为

模型参数可以根据式（4）～式（7）进行求解。在校正的过程中，利用已有的误差来预报未来6 h误差，并对原来的预报结果进行修正；则，经过校正后的潼关站含沙量预报值为

3.4 含沙量过程预报误差评定指标

由于含沙量变化的影响因素更为复杂，加之含沙量过程预报还处于探索阶段，目前尚缺乏评价含沙量预报模型的合理标准[1]。为此，本文借鉴洪水过程预报中常用的精度评价指标，对含沙量过程预报精度进行评定[5]:①量值评定，包括沙峰、沙峰滞时、沙峰相对误差；②过程评定，即比较含沙量预报过程线和实测含沙量过程线的拟合程度。本文采用确定性系数评定，计算公式为

式中，Sc为预报误差值的均方差；σy为预报要素值的均方差；yi、y分别为实测含沙量、预报含沙量；为实测含沙量的均值。

3.5 模型检验

模型选取了潼关1980年～2005年间的12场泥沙过程作为训练样本。选取训练次数为10000，学习速率为0.01，动量因子为0.9作为训练参数对训练样本进行训练。利用训练样本率定出的神经网络各节点的权值与阈值对率定场次进行模拟。通过模拟的含沙量序列与实测含沙量序得出误差序列，并采用递推公式对误差自回归实时校正模型的参数进行估计。误差自回归实时校正模型参数的率定结果见表1；确定性系数、沙峰预报值和沙峰滞时如表2所示；同时选用训练样本以外的5场（19860629、19870824、 19890811、 19900710、 20030825）实测泥沙过程进行验证，对比校正前与校正后的预报结果。验证结果如图1～5所示。

表1 误差自回归模型参数

表2的分析结果表明:①校正后的沙峰相对误差均比校正前有所降低（除了19870824），其中19860629、19900710两场尤为明显，并且相对误差均控制在20%以内；②校正后的沙峰滞时总体较大，甚至比校正前的沙峰滞时还大，预报沙峰出现时间相比于实测沙峰出现时间均有较大偏离；③校正后的确定性系数大幅度提高，除2003025这场的确定性系数为0.687外，其余场次的确定性系数均在0.7以上。另外，图1～5也表明，校正后的预报含沙量过程与实测含沙量过程线拟合程度比校正前拟合程度更好。通过以上分析可知，校正后的泥沙预报精度，较之校正前的预报精度有较大提高。

表2 验证期模型预报校正前、后结果

图1 潼关站 “19860629”场次各序列含沙量过程

图2 潼关站 “19870824”场次各序列含沙量过程

图3 潼关站“19890811”场次各序列含沙量过程

图4 潼关站“19900710”场次各序列含沙量过程

图5 潼关站“20030825”场次各序列含沙量过程

4 结语

（1）在分析黄河流域龙门—潼关区域河流产沙规律的基础上，建立以龙门站、河津站、华县站的含沙量和区间降水为输入，拓扑结构为4-6-1的BP网络模型。同时，为了改善BP模型的预报精度，根据误差序列建立了误差自回归模型，对BP网络的预报结果进行校正，并将该模型应用于潼关站沙量过程的模拟预报。

（2）应用结果表明，校正后的泥沙预报精度，较校正前的预报精度有了较大提高。校正后的沙峰相对误差均控制在20%以内，其中，19860629和19900710号泥沙过程的沙峰相对误差分别由校正前的-40.1%和31.4%降低到校正后的-10.3%和12%；同时，校正后的确定性系数均在0.68以上，5场验证洪水的平均确定性系数由校正前的0.35提高到校正后的0.76，预报精度整体上有显著提高；另外，单场次泥沙预报精度也大幅提高，如19860629和19870824号泥沙过程，确定性系数由校正前的0.171和0.318提高到校正后的0.771和0.873。

（3）校正前后，5场泥沙模拟预报的沙峰滞时均偏大（除20030825外）。这可能与模型构建时，取各场次泥沙过程中各控制站沙峰传播时间和区间降雨的影响滞时的均值作为模型总体的沙峰传播时间和降雨影响滞时有关。针对这一不足，在未来泥沙过程预报中尚需进一步研究改进。

［1］金双彦.黄河中下游泥沙预报模型研究［D］.南京:河海大学，2007，12.

［2］李怀恩，樊尔兰，沈晋，等.逆高斯分布瞬时输沙单位线模型［J］.水土保持学报， 1994， 8（2）:48-55.

［3］石宝，秦毅，凌燕.响应函数模型在含沙量预报中的应用［J］.水土保持通报， 2008， 28（2）:104-105.

［4］包为民.概念性汇沙模型初探［J］.河海大学学报， 1990， 18（6）:24-29.

［5］毛倩倩，梁忠民，霍世青，等.黄河中游龙门含沙量过程统计预报模型研究［J］.水电能源科学， 2012， 30（4）:83-86.

［6］窦国仁.潮汐水流中悬沙运动及冲淤计算［J］.水利学报，1963（4）:13-24.

［7］梁国亭，钱意颖.黄河泥沙数学模型的研究及应用［J］.水文，2000， 22（9）:7-9.

［8］陈集中.应用人工神经网络BP模型预测乌江流域年平均含沙量［J］.水文， 2005， 25（4）:6-9.

［9］张小峰.流域产流产沙BP网络预报模型的初步研究［J］.水科学进展， 2001， 12（1）:17-22.

［10］田景环，王文君，徐建华.基于BP算法的龙门站含沙量预报模型［J］.人民黄河， 2008， 30（3）:26-27.

［11］李正最，谢悦波.基于支持向量机的洞庭湖区域水沙模拟［J］.水文， 2010， 30（2）:44-49.