切线泵全三维湍流数值模拟

2013-10-19王庆方

河南科技 2013年8期

王庆方张宁蒋兵

(1.国家泵类产品质量监督检验中心，山东淄博 255200;2.淄博市博山区产品质量监督检验所，山东淄博 255200)

切线泵，又称为部分流泵，是一种用于输送小流量高扬程介质的离心泵，其流量—扬程特性曲线平坦，即能达到变流恒压效果，解决了一般离心泵小流量超压问题。在小流量、高扬程的低比转速泵领域，切线泵日益取代离心泵。特别是其可靠性高等独特性能，现已被广泛应用于航空、航天、石油、化工、消防等领域[1-2]。

本文通用定常方法对切线泵进行了全三维湍流数值模拟，得到其内部流动的主要特征，可以对泵内部流场进行分析进而对设计进行改进，为改进该类型泵提供了依据。

1 数学模型

1.1 控制方程

叶轮相对于进水部分、蜗壳、出流管道是旋转的，采用多重参考系模型，考虑粘性假定，连续方程和动量方程可以写成笛卡儿张量形式。

连续方程为

动量方程为

式中，ρ是流体密度;xj分别代表各坐标分量x，y，z;uj，ui代表平均相对速度分量u，v，w;p* 是包括紊动能κ和离心力的压力;ωj是角速度;εijk是张量;μe是有效粘性系数，它等于分子粘性系数μ加上紊动涡粘性系数μt，即

1.2 湍流模型

为了确定有效粘性系数μt，使用标准κ-ε紊流模型，它以紊动能κ和耗散率ε的输运方程为基础。

上式中，pk是紊动能的生成项，被定义为

在上述紊动模型方程中，附加的经验常数取:

Cμ=0.09，C1=1.44，C2=1.92，σK=1.0，σε=1.3。

本文选用标准κ-ε湍流模型，运用有限体积法离散控制方程，采用分离隐式计算器对切线泵进行数值模拟。

1.3 边界条件及计算方法

进口条件采用压力进口，即在进口处给定一个进口压力。出口条件采用质量流量出口的边界条件。固壁条件采用无滑移固壁边界条件，并使用标准壁面函数法确定固壁附近的流动。旋转叶轮与静止进水管之间、旋转叶轮与静止蜗壳之间的耦合均采用多重坐标系隐式方法分布的分析。

本文利用多重坐标系，采用三维定常湍流计算方法进行模拟。压力项采用标准格式，速度项、紊动能项和紊粘系数项采用二阶迎风差分格式，速度和压力耦合采用SIMPLE算法[3]，实现速度与压力的耦合。

2 几何模型及网格划分

本文研究对象为QXB2×110-7的切线泵，主要由进水段、叶轮、蜗壳、出水段组成，主要的设计参数为:H=220m，Q=7m/h，n=2900r/min。该泵采用开式径向直叶片叶轮，蜗壳采用环形蜗壳。

本文中切线泵的流道模型在三维造型软件Pro/E中进行造型。导入ANSYS12.0软件中，利用CFX模块对模型进行设置，利用其中的MESH功能对模型进行网格划分整个计算区域的网格数为233746。网格划分如图1。

图1 计算网格系统Fig.1 Calculational grid system

3 数值模拟结果及分析

3.1 压力分布

图2(a)，(b)分别为首级、次级叶轮流道和蜗壳流道中心截面的静压分布图。图中显示叶轮各相邻叶片之间流道静压分布不同，叶轮进口前静压分布已不均匀，每个叶道中随半径的增大，压力逐渐上升。叶道内静压分布随半径的增加且成明显的层状分布[4]。在蜗壳内静压随半径的增加不断增大，且靠近蜗壳扩散管出口的流道进口前静压较小。切线泵涡壳内的旋转液体与叶轮之间基本没有相对流动。

图2 (a)(b)首级、次级叶轮流道和蜗壳流道中心截面的静压分布Fig.2 (a)(b)Static pressure distribution on middle section of the first and second stage impeller and spiral

图2(c)，(d)分别为首级、次级叶轮叶片压力图，图中，叶片表面的压力分布从进口到出口沿半径方向逐渐增加，与前两图保持一致。次级叶轮叶片的表面压力明显大于首级叶轮叶片的表面压力。

这符合切线泵的工作原理。每当单个叶道与扩散管接通的瞬间，就将最外层的流体的流体以接近周速的速度抛出，由于液体是连续的，则必将从进口处补充液体，层层推进[4]。

图2 (c)(d)首级、次级叶轮叶片的静压分布Fig.2 (c)(d)Static pressure distribution of the first and second stage impeller

3.2 叶轮内速度分布

图3(a)，(b)分别为首级、次级叶轮流道内速度矢量图。图3(a)、(b)中叶轮各叶道均存在明显的涡，这是由于叶轮流道内流体的相对运动引起的二次流。由于蜗壳内充满了循环流体，叶道内的流体排卸受阻，其内部流动就开始趋于复杂，出口出现明显回流，产生明显的涡[5]。靠近蜗壳扩散管出口的流道进口速度明显比其他流道进口速度大。每当单个流道与扩散管接通的瞬间就将最外层液体沿切向抛出，同时有液体从叶轮进口处补充进来。观察首级、次级叶轮流道进口速度矢量，可以看到图3(a)、(b)中叶轮各叶道进口处存在涡区，且各进口处有明显回流，使得叶轮流道内的水力损失大大增加。流动非常复杂，叶轮各叶片进口处流动速度变化很大，流动产生很大的冲击损失。叶轮各个流道的流动情况差异也很大，叶轮内流出的流体与蜗壳内的流体混合时也产生了较大的混合损失。

图3 首级、次级叶轮流道内速度矢量图Fig.3 Velocity vector in the first and second flow channel

3.3 蜗壳内速度分布

图4(a)、(b)分别为首级、次级叶轮外蜗壳中间截面喉部的流动矢量图。蜗壳喉部排出的流体由蜗壳内的循环流体和叶道直接排出的流体两部分组成，前一部分流体在蜗壳内经过充分的能量交换，所具有的能量较均匀，后一部分流体没有经过充分的混合，两者能量的差别较大。两股流体在蜗壳出口区域的混合引起了蜗壳喉部的不稳定流动。图中，蜗壳喉部的流动非常复杂，靠近隔舌附近速度大小、方向均发生了剧烈的变化，隔舌附近的速度远小于其它部位，说明隔舌处冲击损失很大，在蜗壳的隔舌附近区域是引起震动和噪声的主要区域。

图4 首级、次级叶轮外蜗壳中间截面喉部的流动矢量图Fig.4 Velocity vector of spiral laryngeal on the middle section of spiral

3.4 性能数据

在CFX中，可以利用流场内的进口总压和出口总压，可以求得水头，求两点水头差可计算出扬程。因此，部分流泵的扬程为Vz为进、出口在垂直方向的距离。

在CFX中，还可以求解叶轮的近似效率，即

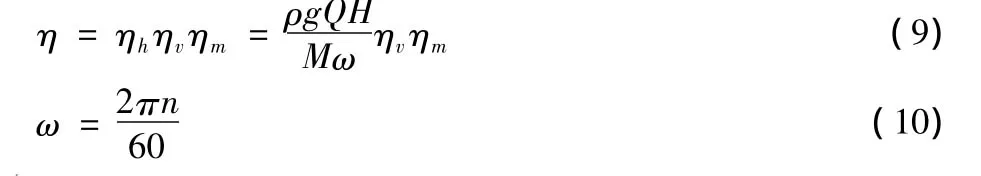
式中，n为轴转速;ω为旋转角速度;M为叶轮叶片绕轴转动的力矩;ηv为预估容积率;ηm为预估的机械效率。整个流道的模拟结果如图由上述公式，在CFX中，模拟结果可得到图5所示的性能曲线，性能曲线稳定，从关死点到设计工况点间，运行平坦，工况佳。在设计工况点，设计效率η=17.13%，数值模拟效率值为η=18%，误差为4.8%，在允许误差范围之内，设计合理。