兼顾阻尼抑制和电压支撑的动态无功补偿装置控制方法

袁志昌，柳勇军，黎小林，许树楷

（1.清华大学 电机工程与应用电子技术系，北京 100084；2.南方电网科学研究院，广东 广州 510080）

0 引言

动态无功补偿装置[1-3]是现代电力电子技术在电力系统中的典型应用，包括以晶闸管为开关器件的静止无功补偿器（SVC）和以可关断器件（IGBT、IGCT）为开关器件的静止同步无功发生器（STATCOM）[4-6]，这些设备可以帮助电网实现动态无功连续调节、提高电网电压稳定水平、抑制线路低频功率振荡，是电网实现可控化和智能化的主要手段之一。

从国内外应用情况看，动态无功补偿装置主要应用于提高受端负荷中心的无功支撑和电压稳定控制，在这种场合通常采用恒电压控制。随着研究的深入和应用的推广，利用动态无功补偿装置抑制低频功率振荡的研究受到关注[7-16]。低频功率振荡的发生会到危及电力系统的稳定运行[8]，随着大区电网的互联和电力系统规模的扩大，低频振荡日趋严重，且出现了频率更低、危害更大的区间低频振荡现象，对动态无功补偿装置进行二次附加阻尼控制[9-16]是解决低频功率振荡问题的一种有效手段。

当动态无功补偿装置需要同时解决输电线路低频功率振荡和电压稳定问题时，面临一个难题，因为阻尼低频功率振荡和保持母线电压稳定这2个控制目标对动态无功补偿装置的无功输出要求往往不完全一致，而采用母线频率或线路功率作为反馈进行阻尼控制时，在一个振荡周期内有2个1／4周期时间里阻尼控制和电压控制对无功方向的需求相反。现有的控制方法未能有效解决两者的协调问题，往往因为过于追求阻尼控制的效果而造成电压大范围波动、超出许可范围甚至引起电压失稳问题。现有的一些动态无功补偿装置的阻尼控制方法由于没能解决与电压稳定控制的协调配合问题，控制效果都不理想。

1 动态无功补偿装置控制方法

典型的动态无功补偿装置控制方法可以用图1表示，其中根据电网的电压Upcc、频率fpcc、功率Pline等信息计算无功电流参考值iqref的环节通常被称为系统级控制，而图中的其他部分通常被称为装置级控制。装置级控制由2条支路构成：一条是无功电流反馈环节，无功电流参考值iqref和测量值iq的差值经过PI调节器（Kp1、Ki1分别为比例系数和积分系数），再累加上有功电流测量值id与连接电抗ωL的乘积，得到STATCOM需要输出的q轴电压eq；另一条是有功电流反馈环节，有功电流参考值idref和测量值id的差值经过PI调节器（Kp2、Ki2分别为比例系数和积分系数），再累加上无功电流测量值iq与连接电抗ωL的乘积，得到STATCOM需要输出的d轴电压ed。有功电流支路通常用来控制STATCOM的直流电容电压值保持恒定，因此idref来自于直流电压Udc的PI控制结果，Udcref为直流电压参考值，Kp3、Ki3分别为直流电压PI控制器的比例系数和积分系数。

图1 STATCOM典型控制方法原理框图Fig.1 Schematic diagram of typical STATCOM control

根据不同的应用场景，动态无功装置需要向电网提供有差异的控制功能。动态无功装置应用于受端负荷中心时，主要向电网提供动态无功支撑和暂态电压稳定控制，其系统及控制通常采用图2所示的恒电压控制。计算接入电网点的电压Upcc与参考电压Uref的差值ΔU，该差值ΔU经过超前滞后校正和PI调节计算出所需的无功电流指令值iqref。

图2 恒电压控制原理图Fig.2 Principle of constant voltage control

随着研究的深入和应用的推广，利用动态无功补偿装置抑制低频功率振荡的研究受到关注。图3所示是最简单的利用动态无功补偿装置抑制低频功率振荡的控制方法，这种方法中，首先测量电网点的频率 fpcc，计算fpcc与参考频率 fref的差值 Δf；Δf经过一阶惯性函数、超前滞后校正、带限幅的增益环节计算出所需的无功电流指令值iqref。有时也用受控线路的功率值Pline替代频率进行反馈阻尼控制。其基本原理是根据受控线路的功率或频率的变化，按照简单的PI反馈控制器调节无功补偿装置的输出，通过实时改变接入点的电压来调节线路的传输功率，当线路传输功率降低时，使无功补偿装置发出容性无功、支撑母线电压以提高传输功率，相反当线路传输功率增大时，使无功补偿装置吸收感性无功、降低母线电压以降低传输功率。

图3 阻尼控制原理图Fig.3 Principle of damping control

这种控制方法存在一个问题，抑制线路低频功率振荡的同时可能造成接入点母线电压的振荡。这是因为线路传输有功功率降低时，消耗无功功率相应降低，接入点母线电压会升高，此时为了抑制功率振荡需要提高线路传输功率，这是通过注入容性无功实现的，然而容性无功的注入会进一步提高接入点电压；类似地，当线路传输功率增加时，接入点电压会随着线路消耗的无功功率增加而降低，图3所示的控制方法要求无功补偿装置吸收感性无功，这将进一步降低系统电压。可见，图3所示方法在抑制线路功率振荡的同时，可能加剧接入点母线电压的振荡，这对保持电网的电压稳定是非常不利的。

图4为另外一种常见的抑制低频功率振荡的方法。这种方法中，计算受控线路频率测量值与参考频率的差值Δf，Δf依次通过一阶惯性、超前滞后校正和带限幅的增益得到阻尼控制所需的电压附加分量Udamp，将该附加分量Udamp引入如图2所示的恒电压控制中，其后的控制流程与图2所示方法相同。在这种方法中，阻尼控制是通过附加频率的反馈量来实现的，因此也被称为附加阻尼控制。当线路发生低频功率振荡时，电压分量相对较小，功率振荡分量占据主导，其控制效果类似于图3所示的方法，同样无法避免阻尼控制对电压稳定控制的负面影响。

图4 附加阻尼控制原理图Fig.4 Principle of supplementary damping control

2 阻尼控制与电压控制的关系

本文通过图5所示的简单系统分析动态无功补偿装置应用于抑制低频功率振荡和电压稳定控制时面临的问题。图5系统由单机无穷大系统加装STATCOM构成，发电机采用经典二阶模型，暂态电抗后的电动势E′恒定，相位为δ，暂态电抗和变压器的电抗之和为XG，发电机输出有功和无功分别为Pe、Qe。无穷大系统的电压为U∠α。不失一般性，假设STATCOM接入传输线路中间，距离发电机母线的阻抗为XL，距离电网母线的阻抗为XS。记STATCOM 并网点电压为US∠0°，流入STATCOM的电流为IS∠-90°，IS＜0表示STATCOM向电网注入容性无功，IS＞0表示STATCOM吸收感性无功。

图5 有动态无功补偿的单机无穷大系统Fig.5 Single-machine infinite system with STATCOM

首先假设STATCOM未投入运行，此时系统就是一个单机无穷大系统，其状态方程为：

其中，M为发电机转动惯量，ω为发电机角频率，Pm为发电机机械功率，Pe为发电机输出功率，D为发电机阻尼系数，X∑=XG+XL+XS。

假设稳态运行时发电机的功角为δ0，在小扰动的激励下，发电机的功角、频率、电压都会出现低频振荡，可以通过计算功角、频率和电压的摄动量来考察三者之间的相位关系。由式（1）推导可得：

其中，E1=XSE′／X∑，E2=（XG+XL）U／X∑。

可见，发生低频振荡时，线路上电压幅值的振荡相位与功角的振荡相位相反，而角频率的振荡相位是功角振荡相位的微分，即滞后功角振荡相位90°。其相位关系如图6所示（电压为标幺值）。

图6 低频振荡时的电压和频率相位关系Fig.6 Curve of voltage vs.frequency during low-frequency oscillation

STATCOM投入运行后，线路传输功率Pe由式（3）决定：

其中，等号右边第1项为无STATCOM时的线路传输功率，第2项为STATCOM向系统注入无功电流IS后对传输功率的改变量。可见，改变STATCOM无功电流的方向，可以改变线路传输功率的幅值，进而实现对发电机的阻尼控制。根据式（3），当振荡过程中频率高于额定频率时，需要增加线路传输功率以维持发电机能量平衡，此时STATCOM应该发无功；当频率低于额定频率时，需要减小线路传输功率，此时STATCOM应该吸无功。这一关系如图6中的频率曲线所示，t1至t3时段内，STATCOM应该吸无功，t3至t5时段，STATCOM应该发无功。

而对于电压稳定控制，当电压低于稳态值时，STATCOM应该发无功以提高并网点电压；当电压高于稳态值时，STATCOM应该吸收无功以降低并网点电压。这一关系如图6中的电压曲线所示，t1至t2和t4至t5这2个时段应该发无功，t2至t4时段内应该吸无功。

可见，由于振荡时角频率的相位与电压幅值的相位之间相差90°，造成阻尼低频功率振荡和保持母线电压稳定这2个控制目标对动态无功补偿装置的无功输出要求不完全一致，在一个振荡周期内有2个1／4周期时间里阻尼控制和电压控制对无功方向的需求相反，如图6中t1至t2时段、t3至t4时段。

3 协调阻尼和电压的优化控制方法

本文提出一种动态无功补偿设备的电压和阻尼协调控制方法，可以兼顾电力系统对动态稳定和电压稳定的控制要求。该方法将受控母线电压和频率作为动态无功补偿设备的控制输入信号，在电压控制和阻尼控制两者出现矛盾的时候，通过协调优化算法，选取最优的无功控制指令，防止阻尼控制引起电网电压超标，实现电压和阻尼协调控制。

图7所示为协调控制方法的原理图，输入信息为受控母线的电压和频率值，经由电压稳定控制、阻尼控制和协调控制3个模块计算出动态无功装置所需的无功电流参考值。

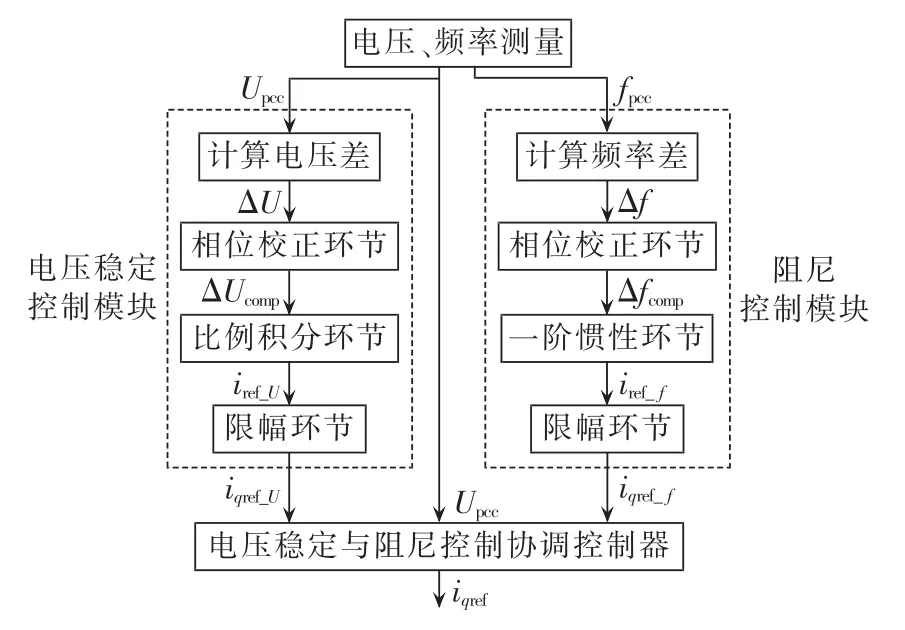
图7 电压和阻尼协调控制方法Fig.7 Coordinated damping control and voltage control

图7中电压稳定控制、阻尼控制2个模块内部的控制结构与图2、图3所示结构相同。对控制性能有关键影响的协调控制模块的控制算法如下。

（1）将接入点电压Upcc、电压控制所需的无功量iqref_U，阻尼控制所需的无功量iqref_f输入到电压控制和阻尼控制协调控制模块。

（2）条件1：动态无功补偿装置接入点母线电压Upcc低于0.9 p.u.或高于1.1 p.u.时，可判定系统偏离稳定状态较大，此时电压控制是首要目标，选取电压控制模块的输出作为动态无功补偿装置的无功参考值，即 iqref=iqref_U。

（3）条件2：Upcc高于 0.9 p.u.而低于 1.1 p.u.时，按以下逻辑依次判断阻尼控制与电压控制之间是否存在矛盾。

a.如果母线电压与参考电压的差值ΔU小于-0.05 p.u.（即偏离稳态电压的最大许可值，该值可根据现场需要调整），且阻尼控制模块的输出iqref_f大于0，这意味着电压已跌落至稳态允许值之下，而此时阻尼控制仍要求动态无功补偿装置吸收感性无功，可以判断2种控制模式对无功的需求存在矛盾，此时以电压控制为优先，选取电压控制模块的输出作为动态无功补偿装置的无功参考值，即iqref=iqref_U。

b.如果母线电压与参考电压的差值ΔU大于0.05 p.u.，同时阻尼控制模块的输出iqref_f小于0，这意味着电压已升高至稳态允许值之上而同时阻尼控制却要求动态无功补偿装置发出容性无功，同样地，可以判断2种控制模式对无功的需求存在矛盾，此时优先保证电压控制，选取iqref=iqref_U。

c.若a、b 2种条件均不成立，则可判断该时刻电压控制和阻尼控制对无功的需求不存在矛盾，为了保证阻尼控制的效果，优先选取阻尼控制模块的输出作为动态无功补偿装置的无功参考值，即iqref=iqref_f。

（4）动态无功补偿装置无功参考值iqref发送至下一级（装置级）控制器，控制装置无功输出。

4 仿真分析

在如图5所示的单机无穷大系统中对本文所提的电压和阻尼协调控制策略开展仿真研究。STATCOM接入输电线路中间位置。仿真系统中发电机参数（以发电机额定容量和额定电压为基值）为：Xd=1.8，Xq=1.7，X1=0.2，Ra=0.002，X′d=0.3，X′q=0.55，T′d0=8 s，T′q0=0.4 s，X″d=0.25，X″q=0.25，T″d0=0.03 s，T″q0=0.05 s，容量为 600 MV·A，H=6.5 MW·s／（MV·A）。线路参数（以发电机额定容量和额定电压为基值）为：XG=0.3，XL=0.5，XS=0.2。STATCOM 参数（以自身额定容量和额定电压为基值）为：容量为100 Mvar，无功响应时间为20 ms，连接电抗为0.15。发电机未考虑励磁和调速系统，且阻尼力矩系数相对较小，发生线路故障时引起低频功率振荡。

为了便于比较，仿真研究了无STATCOM控制器、有STATCOM并按频率反馈进行阻尼控制、有STATCOM并按照电压阻尼协调控制3种情况。图8给出了接入点母线电压情况，图9给出了母线频率情况，两图纵轴均为标幺值。从图8可以看出采用按频率反馈的阻尼控制后，电压波动的阻尼大幅改善，但是在振荡的前2个周期内，电压的振荡幅度明显大于无功STATCOM控制器的情况，这体现了恒电压控制与阻尼控制对STATCOM无功需求不完全一致的矛盾。采用了电压和阻尼协调控制后，当电压超出稳态允许范围以外且恒电压控制与阻尼控制不一致时，优先保证恒电压为目标，因此在振荡的前2个周期内，电压振荡的波峰被有效地“削”平了，避免出现欠压或过压。从图9的频率振荡情况看，采用电压和阻尼协调控制策略后，其对阻尼的改善效果略差于按频率反馈控制，但是两者均较无功STATCOM时有明显改善。从总体效果看，电压和阻尼协调控制策略牺牲了部分阻尼控制效果，换取了电压不出现过压和欠压，这种折中是值得的。

图8 STATCOM接入点电压曲线Fig.8 Voltage curve of PCC

图9 STATCOM接入点频率曲线Fig.9 Frequency curve of PCC

5 结论

电网发生低频功率振荡时，角频率的相位与电压幅值的相位之间相差约90°，造成阻尼低频功率振荡和保持母线电压稳定这2个控制目标对动态无功补偿装置的无功输出要求不完全一致，在一个振荡周期内有2个1／4周期时间里阻尼控制和电压控制对无功方向的需求相反。为了兼顾阻尼控制和电压控制这2种目标，可以根据动态无功补偿装置接入点的电压和频率值实时判断2种控制目标是否出现矛盾。当2种控制所需无功方向相反时，应该优先选取稳定电压作为控制目标，这样做的结果会牺牲部分阻尼控制的效果，但是可以确保电压控制的稳定。