Boost PFC变换器快时标分岔的控制方法
2013-10-19郑连清鲁思男
郑连清,鲁思男
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.重庆市电力公司,重庆 400039)
0 引言
由于开关器件自身的特性和反馈控制环节的引入,Boost功率因数校正(PFC)变换器成为一种强非线性系统[1]。近年来,国内外学者采用非线性动力学对Boost PFC变换器进行了研究并取得了一些成果[1-6]。已有的研究发现随着PFC变换器中某些参数的变化,系统会产生快时标(fast-scale)下的不稳定现象,即在开关频率附近发生分岔,这些分岔现象的存在会严重影响PFC变换器的工作性能。斜坡补偿法是最常用的方法,但其应用存在经验设计行为,若补偿强度设计不当,便会导致过度补偿现象的发生,使变换器的功率因数值急剧下降。利用参数微扰法设计的斜坡补偿强度[7-9],由变换器中的主要参数(输出电压、开关周期和电感值)决定,不仅避免了过度补偿,而且在控制快时标分岔的同时维持了较高的功率因数值,不过此方法仍然存在一些不足之处。
随着功率变换器控制技术的快速发展,利用智能控制技术来完成变换器的分岔控制成为可能,本文借鉴近几年来国内外滑模控制的研究成果[10-13],采用双积分滑模对其分岔现象进行控制。仿真结果表明,双积分滑模法很好地弥补了参数微扰法在快时标分岔控制中的不足,得到了更好的控制效果。此外,双积分滑模控制通过增加控制器的阶数改善了系统的稳态误差,并降低了滑模控制中的抖振现象,同时获得了更高的功率因数值。
1 频闪映射建模及分岔现象

图1 峰值电流型Boost PFC变换器电路图Fig.1 Circuit of Boost PFC converter in peak-current control mode
图1为峰值电流型Boost PFC变换器的电路。图中,uin为输入的工频电压,us为整流后的电压,iL为电感电流,uC为电容两端的电压,uo为输出电压,Uref为参考电压,iref为参考电流,k1、k2为控制增益参数。
该变换器工作在连续模式,在第n个开关周期内,输入电压 usn为:。其中,Um为输入电压的峰值,ω=100π,T为开关周期。由于开关频率远远大于电源频率,可以近似认为一个开关周期内输入电压不变,记,p∈[0,1] 。
定义状态向量 x=[iLuC]T=[x1x2]T,则有:

开关条件所对应的切换平面为:

频闪映射的示意图如图2所示,设xn为初始状态,在 tdn时刻到达切换面 h(x,t)=0,此时占空比为 dn。

图2 频闪映射示意图Fig.2 Schematic diagram of stroboscopic mapping
当 nT<t≤tdn时,有:
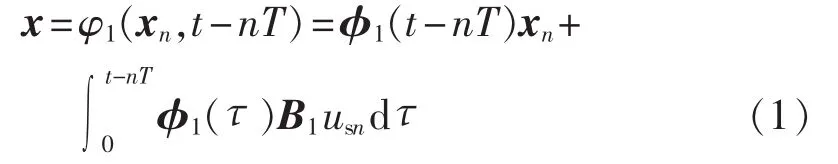
当 tdn<t≤(n+1)T 时,有:

其中,φi(τ)=exp(Aiτ);i=1,2。
联立式(1)和式(2)可解出xn和xn+1的数学关系:

再加上切换面满足的条件:
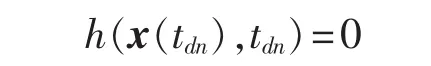
就得到了Boost PFC变换器的离散迭代映射模型。
图3(a)为电感电流在 t∈[0.05,0.06] s内的频闪采样波形,图3(b)为输入电压和电感电流的相轨迹。对比观察两图可以看到,随着输入电压的增大,电感电流从混沌态变为二周期态,在0.0528 s处进入单周期态,然后在0.0578 s处再次进入二周期态,最后发生边界碰撞分岔以非光滑的方式直接变为混沌态。

图3 电感电流的分岔现象Fig.3 Bifurcation of inductor current
降低输入电压,给出此时的电感电流频闪采样图,如图4所示。在整个1/2个工频周期内电感电流都处于快时标不稳定状态,THD值明显增大。

图4 降低输入电压后电感电流的分岔现象Fig.4 Bifurcation of inductor current when uindecreases
2 参数微扰控制
选取变换器的参考电流iref为补偿信号,其斜坡补偿的原理如图5所示。

图5 斜坡补偿原理图Fig.5 Principle of ramp compensation
在一个开关周期内,即从t=nT到t=(n+1)T,开关导通,电感电流上升,直到等于i*ref,开关断开,电感电流下降,令in和in+1分别为t=nT和t=(n+1)T时刻的电感电流,可以得到in和in+1的表达式:


将上式分解、整理合并,并保留其中一阶微扰量得:

其中,θ=ω′t,θ′∈[0,π] 。由式(4)可以得到微扰量Δin+1与Δin之间的迭代关系:

很明显地可以看到特征根为:

由非线性动力学理论可知,当λ位于复平面的单位圆时,变换器处于稳态,当λ沿着负实轴方向穿越单位圆时,便会发生倍周期分岔,所以λ=-1是倍周期分岔的临界值,此外,输入、输出电压满足关系式,把这2个关系式同时代入式(5)中可以得到:


为了让变换器在这个工频周期内都保持稳态运行,令临界状态下的相角等于0,式(7)可以化简为:
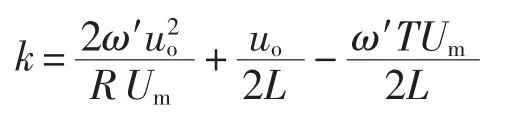
斜坡补偿信号的幅值为:
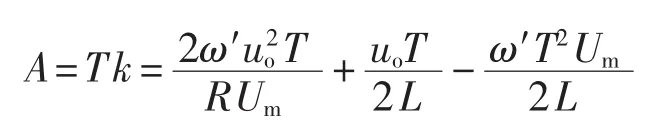
经计算得出补偿信号的幅值A=1.124。
3 双积分滑模控制
3.1 控制器的设计
双积分滑模控制的Boost PFC变换器原理如图6所示。
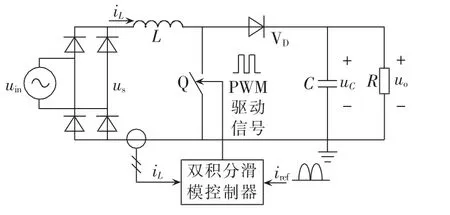
图6 双积分滑模控制的Boost PFC变换器电路图Fig.6 Circuit of Boost PFC converter with double integral sliding mode control
此控制器采用电流误差x1、电流误差的积分x2和其双重积分x3作为变量。状态变量定义如下:
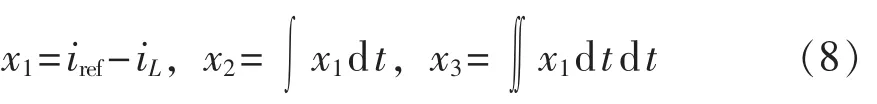
令控制信号u为1或0,u=1表示开关导通,u=0表示开关断开。滑模面定义为:
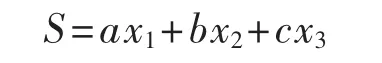
其中,a、b、c是滑模系数。S的一阶导数为:


等效控制[14]中,用一个连续信号来代替离散信号,其中。
把式(8)代入式(9)中可得:
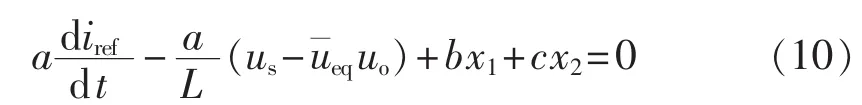
解式(10)可得:

由李雅普诺夫稳定性分析确定滑动模态存在条件。定义李雅普诺夫函数为,要使系统运行在滑动模态,必须满足:。


合并式(12)和式(13),可以得到:

上式即为系统滑动模态存在的条件。
3.2 滑模系数的选择
把式(11)变形为:

再把式(14)转化为频域表示:

图7给出了式(13)的传递函数框图。
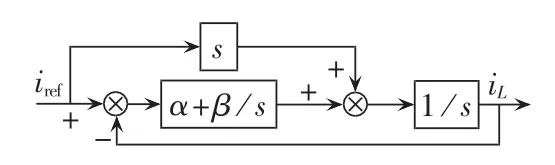
图7 双积分滑模控制的电流环框图Fig.7 Block diagram of current loop under double integral sliding mode control
选取52°的相角裕度设计补偿环节,利用MATLAB绘出其伯德图(图8所示),同时考虑滑动模态的存在条件,最后确定 α=2×105,β=4×108。

图8 双积分滑模控制的电流环伯德图Fig.8 Bode diagram of current loop under double integral sliding mode control
4 仿真结果比较
采用参数微扰控制时,Boost PFC变换器的电感电流波形、输入电压和电感电流的相轨迹见图9。
观察图9(a)可以看到,在整个1/2个工频周期内电感电流都没有出现分岔现象,但在0.05 s和0.06 s附近出现了过零死区。从图9(b)中明显地观察到电感电流的中心偏移现象,即一个电感电流值对应了2个输入电压值。若补偿后的电感电流为标准的正弦形,会以0.055 s为中心线左右完全对称,即出现一个电感电流值对应一个输入电压值的线性关系。过零死区和中心偏移现象都影响了补偿效果,此时的THD值为15%。
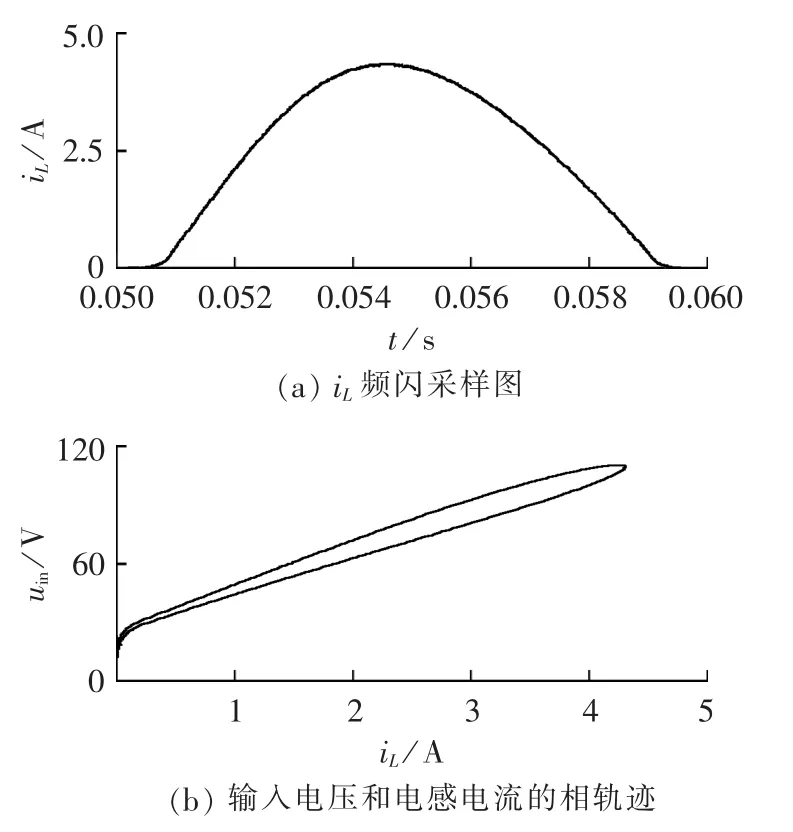
图9 参数微扰控制的效果Fig.9 Performance of small parametric perturbation control
降低输入电压后,补偿效果如图10所示。过零死区和中心偏移现象仍然存在,而且电感电流也随着输入电压的降低而降低。
采用双积分滑模控制时,控制效果如图11所示。此时的电感电流在整个1/2个工频周期内没有分岔现象,也没有出现过零死区和中心偏移现象。经过FFT分析,THD值为0.6%。
降低输入电压,图12中给出了仿真结果。从图12中看到,即使降低输入电压,电感电流仍然没有降低,控制性能较好。
表1对参数微扰法和双积分滑模法的性能进行了对比。表中,功率因数值为位移因数。

图11 双积分滑模控制的效果Fig.11 Performance of double integralsliding mode control

图12 降低输入电压后双积分滑模控制的效果Fig.12 Performance of double integral sliding mode control when uindecreases

表1 2种控制方法的性能对比Tab.1 Peformance comparison of two control methods
5 结论
本文基于频闪映射法建立了峰值电流型Boost PFC变换器离散迭代映射,利用频闪采样和相轨迹图分析了随着输入电压的减小,系统发生倍周期分岔,最后进入混沌态。然后采用参数微扰法和双积分滑模法对Boost PFC变换器进行了分岔控制。仿真结果表明,参数微扰法虽然有效地避免了变换器快时标分岔现象并提供了一般性的斜坡补偿强度计算公式,但存在过零死区和中心偏移;双积分滑模法在不同参数条件下有效避免分岔现象的同时,弥补了参数微扰法在分岔控制中的不足之处,并使Boost PFC变换器获得了0.99的高功率因数值。双积分滑模控制法在分岔控制中具有以下特点:
a.不需要改变系统参数或施加外部扰动;
b.使Boost PFC变换器获得较高的功率因数值;
c.具有很强的鲁棒性。
该方法的诸多特点,保证了Boost PFC变换器在不同参数条件下运行的稳定性和可靠性。
