基于双端时域信号的过渡电阻在线计算方法
2013-10-19马彦飞程学启邱升孝栾国军张琳琳
丛 伟,马彦飞,程学启,邱升孝,王 葵,栾国军,张琳琳
(1.山东大学 电网智能化调度与控制教育部重点实验室,山东 济南 250061;2.国网山东省电力公司潍坊供电公司,山东 潍坊 261021;3.国网山东省电力公司泰安供电公司,山东 泰安 271000)
0 引言
电力系统中的短路一般都不是金属性的,而是在短路点存在过渡电阻。短路点的过渡电阻是指当发生相间或接地短路时,短路电流从一相流到另一相或从相导线流入大地的途径中所经过物质的电阻,包括电弧、中间物质电阻、相导线与地之间的接触电阻、金属杆塔的接地电阻等。过渡电阻给电力系统故障分析、保护定值整定计算、保护装置的可靠动作带来诸多不利影响[1-5],很多保护装置的误动或拒动都与过渡电阻有关。过渡电阻具有较强的随机性和不可预见性,尤其是经电弧短路的故障,过渡电阻将会间歇出现数值在较大范围内变化的现象[6]。对过渡电阻特性进行在线、实时计算,对于运行人员进行准确的系统分析、掌握过渡电阻变化特性、提高保护装置应对过渡电阻的性能具有重要意义。
国内外学者在过渡电阻计算方法方面做了大量的研究工作。文献[7-8] 提出基于单端电压、电流计算过渡电阻的方法,文献[9] 利用零序电压、电流补偿系数近似值计算过渡电阻,文献[10] 提出基于测量到的有功功率计算过渡电阻的方法,文献[11] 提出利用双端电气量瞬时采样值在故障点位置已知的情况下计算过渡电阻的新方法。其中,文献[7-10] 均采用对称分量法进行计算,受算法特点的限制,计算实时性会受影响。此外,目前多数计算方法都要求已知故障测距结果,计算结果难免存在较大误差。
本文提出一种基于双端时域信号的过渡电阻在线计算方法,在已知故障类型的前提下,采用线路两端从故障发生后到断路器跳闸前的电压、电流时域信号,对过渡电阻值进行在线实时计算。由于工程实际中输电线路长度大多不超过300 km,本文采用输电线路的π型集中参数模型以简化计算,且满足实际工程要求。该方法具有不受故障位置影响、计算响应速度快等优点,仿真结果表明该方法的计算结果具有较高的准确度。
1 单相系统过渡电阻计算方法
图1为一双端电源单相输电系统,线路采用π型集中参数模型。设线路均匀,单位长度的电阻、电感、对地分布电容分别为r、l、c,线路全长为L。假设在距离M侧母线x处的点F发生接地短路,过渡电阻为Rg。从母线M、N处测量得到的两侧电压、电流时域信号分别为 uM、iM和 uN、iN,记故障点处的电压时域信号为uF,流经过渡电阻的电流时域信号为iF。
对故障点F列KCL方程有:

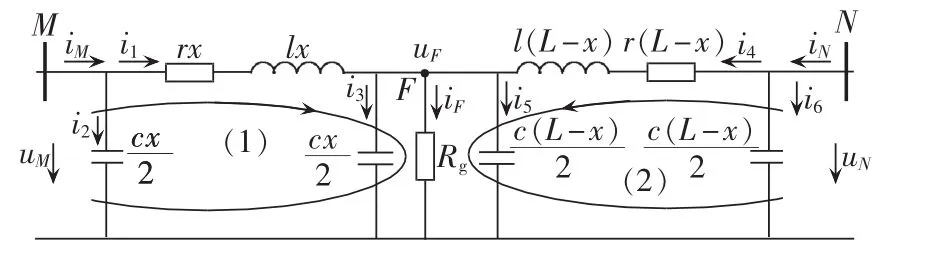
图1 双端单相输电系统Fig.1 Two-terminal single-phase transmission system
对图 1中回路(1)、(2)分别列 KVL方程有:
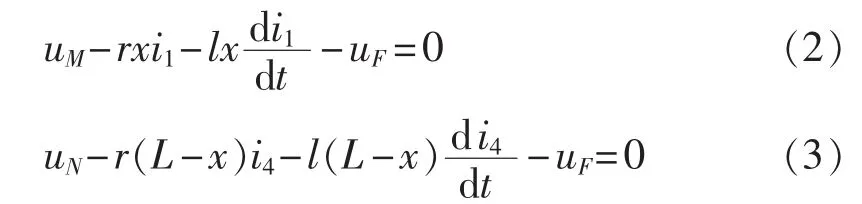
由式(1)可写出故障距离x的表达式:

将式(4)代入式(2)、(3)可得:
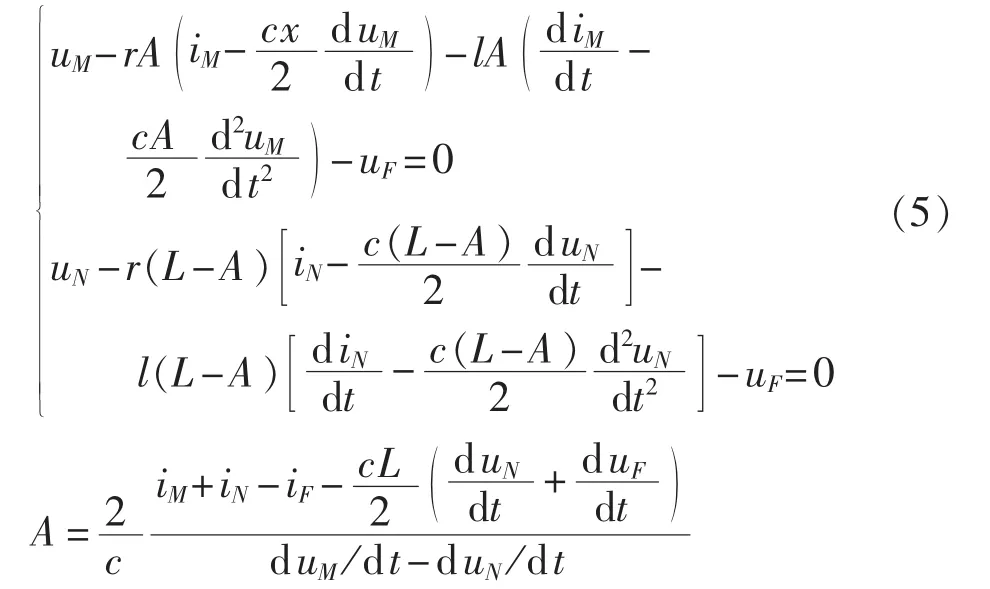
式(5)包含 2 个方程,对应 2 个未知数 uF、iF,由于未知数x已被消去,因此求解过程不受故障测距结果x的影响。将线路两侧的电压、电流时域信号代入式(5),就可求出未知数 uF、iF,则过渡电阻为:

2 三相系统过渡电阻计算方法
在实际的三相电力系统中,除理想的三相短路外,其余故障条件下系统均处于不对称运行状态,为了便于分析,可对三相不对称系统进行解耦,分解为对称的系统后采用与单相系统类似的处理方法求解过渡电阻。
2.1 三相系统的相模变换
本文采用故障发生后至断路器跳闸前故障持续时间内的时域信号来计算过渡电阻值,在该时段内故障点两侧线路参数可视为平衡,则相模变换矩阵可取为常数矩阵[12]。本文采用卡伦鲍厄(Karrenbauer)变换进行解耦,变换矩阵Tm及其逆阵为:
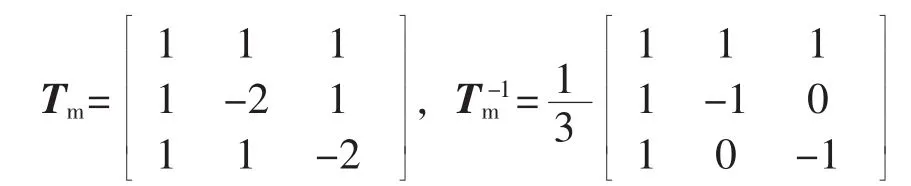
变换后的量分别为0模、1模、2模。取相电压、相电流列向量分别为Up、Ip,模电压、模电流列向量分别为Um、Im,则三相电压与模电压间满足 Um=Tm-1Up,三相电流与模电流之间同样满足Im=Tm-1Ip。
设系统中各个元件的相域阻抗矩阵为Zp,模域阻抗矩阵为Zm,则二者满足如下关系:Zm=Tm-1ZpTm。取相域阻抗矩阵Zp的对角元素为zd,非对角元素为znd。则变换后的模域阻抗矩阵为:

可见,变换后的模阻抗参数与序阻抗参数相等[13]。
采用卡伦鲍厄变换可以将不对称的系统转换为对称系统,得到0模、1模和2模3个相对独立的模网络,每个模网络都可等效为图1所示的结构,只不过对应的参数为模网络参数。针对不同的模网络均可以写出与式(5)类似的表达式,如式(8)所示。

其中,k=0、1、2分别对应0模、1模、2模。
对双端时域电压、电流信号进行相模变换,代入式(8)可以求出故障点的电压模量uFk和流经过渡电阻的故障电流模量iFk,进而求得过渡电阻Rg。
2.2 利用复合模网络求解过渡电阻
由故障分析知识可知,不同故障类型对应着不同的故障边界条件,从而决定了复合模网络的不同连接方式。而复合模网络不同的连接方式,又决定了求解过渡电阻的不同表达式。以单相接地故障为例,根据故障边界条件得到的复合模网络如图2所示。

图2 单相经过渡电阻接地短路的复合模网络Fig.2 Composite modal network with single-phase grounded via transition resistor
由图2得到过渡电阻Rg的表达式为:

同理,发生两相经过渡电阻接地短路故障时,复合模网络如图3所示。过渡电阻的求解表达式为:

图3 两相经过渡电阻接地短路的复合模网络Fig.3 Composite modal network with two phases grounded via transition resistor
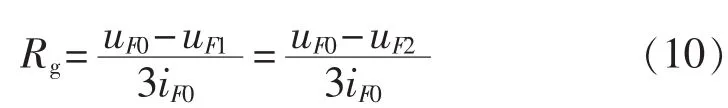
发生两相经过渡电阻短路故障时,复合模网络如图4所示。过渡电阻求解表达式为:
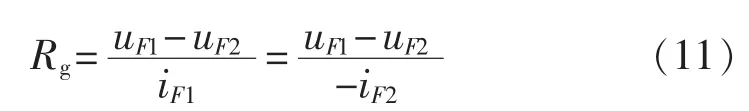
当发生三相短路或三相接地短路时,由于是对称性故障,可直接用图1所示的单相电路进行分析,过渡电阻求解表达式为:

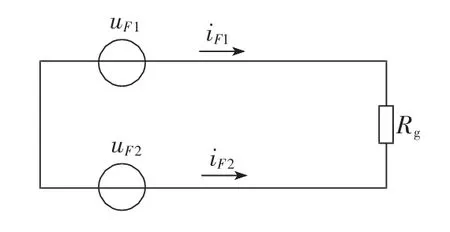
图4 两相经过渡电阻短路的复合模网络Fig.4 Composite modal network with inter-phase short circuit via transition resistor
3 算例仿真
为了验证本文所提算法的正确性和有效性,采用PSCAD/EMTDC仿真软件,搭建如图5所示的500 kV双端电源系统。线路采用π型等效模型,长度为 300 km,参数[14]为:R1=0.019 79ω /km,R0=0.228 46ω /km;ZL+=0.275 14ω /km,ZL0=0.870 97ω /km;ZC+=239.150 9×103Ω·km,ZC0=370.990 5×103Ω·km。

图5 双端输电系统模型Fig.5 Model of two-terminal transmission system
设故障发生时刻为0.5 s,从故障发生到断路器跳开的时间为100 ms,本文就采用这100 ms的时域信号计算过渡电阻,采样频率为2 000 Hz。在计算过程中涉及的一阶及高阶导数计算,均采用3点法前推公式及理查森外推法。本文计算过程最高涉及二阶导数,因此每个计算步长内需要用到连续5个采样点数据。
3.1 算例1
设置故障类型为A相经100ω过渡电阻接地,故障点距离M侧母线50 km。
计算得到的过渡电阻曲线如图6所示。可见故障发生后经过2.5 ms的延时,过渡电阻计算结果为94.26ω,可基本准确追踪到过渡电阻的实际值,且采样频率越高,该延时越小。过渡电阻计算结果的最大值为108.55ω,相对误差为8.55%;最小值为93.05ω,相对误差为6.95%。计算误差主要受导数计算方法和系统采样频率的影响。

图6 50 km处A相经100ω过渡电阻接地时的计算结果Fig.6 Calculated results when phase-A grounded at 50 km via 100ω transition resistance
对计算结果进行正态分布校验如图7所示,图中虚直线表示正态分布的概率分布,+号点线表示过渡电阻计算结果的概率分布,每个+号点的横坐标对应一个过渡电阻计算值,纵坐标为对应的概率分布。由图中可以看出,绝大多数+号点与图中虚直线基本拟合,因此可以得出图6计算结果基本符合正态分布,具体参数估计为:期望值100.76ω,方差3.44ω,期望 0.95置信区间[100.27,101.24]ω,方差 0.95置信区间[3.13,3.82]ω。

图7 图6计算结果的正态分布校验Fig.7 Normal distribution verification for calculated results of fig.6
3.2 算例2
为了分析不同故障位置对本文所提方法的影响,设置故障类型为A相经500ω过渡电阻接地,故障点距离M侧母线分别为50 km、150 km。
计算得到的过渡电阻曲线如图8所示,表1给出了多个故障位置下的仿真计算结果。由图8和表1可见,故障位置对计算结果的影响较小,表明算法的性能基本不受故障位置的影响。

图8 50 km、150 km处A相接地过渡电阻计算结果Fig.8 Calculated transition resistances for phase-A grounded at 50 km and 150 km

表1 50 km、100 km、150 km、200 km处A相接地过渡电阻计算结果Tab.1 Calculated transition resistances for phase-A grounded at 50 km,100 km,150 km and 200 km
3.3 算例3
设置故障类型为A相经时变过渡电阻接地,故障距离M侧母线50 km。
实际系统发生经过渡电阻接地故障时,过渡电阻往往不固定,其值随时间变化,表现出较强的随机性和不可预见性[15]。设过渡电阻的表达式如下:

设故障点距离M侧母线50 km,计算结果如图9所示。
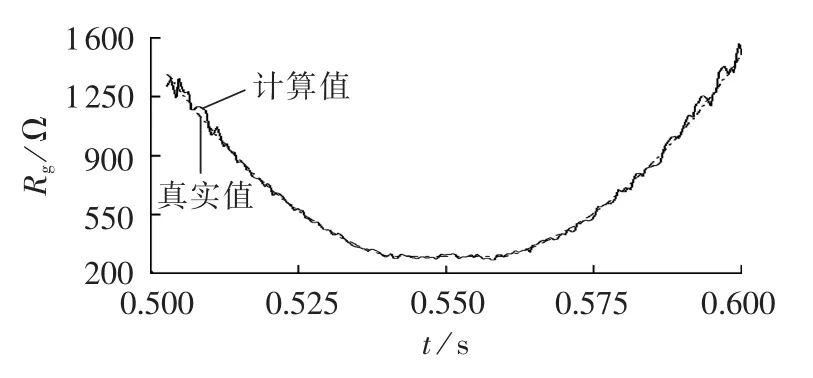
图9 时变过渡电阻计算结果Fig.9 Calculated time-varying transition resistance

其中,Rgc和Rga分别为过渡电阻的计算值和实际值。
定义过渡电阻计算结果相对误差e为:
对过渡电阻计算结果误差进行分析的情况如图10所示,相对误差最大值为5.98%,出现在曲线的拐点处,最小值为0.12%。如果过渡电阻曲线足够平滑,计算误差会进一步减小。可见,本文所提方法具有较好的响应速度和较高的计算准确度。
3.4 算例4
为了验证本文所提方法对不同故障类型的适用性以及对高过渡电阻计算的准确性,设置故障类型分别为单相接地、两相短路、两相短路接地和三相短路,故障距离M侧母线50 km,过渡电阻为2 kΩ。
采用式(9)—(12)进行计算得到的统计结果如表2所示。可以得出,在不同故障类型下计算得到的过渡电阻差别不大,与真实值的误差较小,表现出较好的适用性。
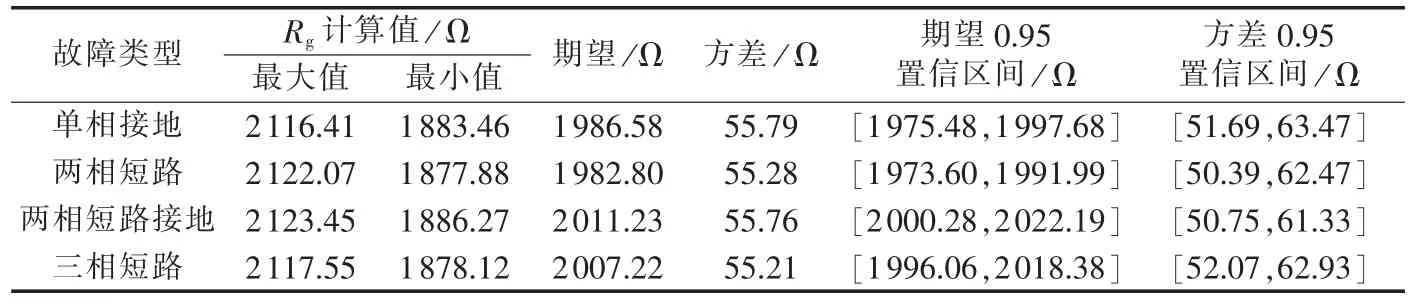
表2 不同故障类型下的过渡电阻计算结果Tab.2 Calculated transition resistance for different fault types
4 结语
本文提出了一种基于双端时域信号的过渡电阻在线计算方法,采用从故障发生到断路器跳开这一时间段内线路两侧的同步时域信号,通过求解微分方程组,对过渡电阻值进行快速、准确的计算,该方法具有如下特点:
a.基于线路两端电压电流的同步时域信号计算过渡电阻,具有所需数据窗小、响应速度快等优点;
b.算法不受系统振荡、非周期分量和谐波的影响,计算结果具有较高的准确性;
c.计算结果不受故障点位置的影响,因此无需获得故障测距的结果,避免了故障测距误差对过渡电阻计算结果准确性的影响;
d.该方法必须与故障选相元件配合工作,适用于各种短路故障类型的过渡电阻计算。
