基于多目标遗传算法的水平井裂缝参数优化

陶 珍，田昌炳，熊春明，刘保磊，彭缓缓

(中油勘探开发研究院，北京 100083)

1 多目标优化遗传算法简介

多目标优化问题与单目标优化问题不同，单目标优化是研究单个函数极值问题，多目标优化则可能要同时优化多个相互冲突的目标函数。多目标优化存在非劣解集(又称 Pareto最优解集)[1－4]。一般情况下，不可能使多个目标同时达到最优，只能在Pareto最优解集中进行协调，得到协调解。

1个大型的多目标优化问题一般如下[5]:

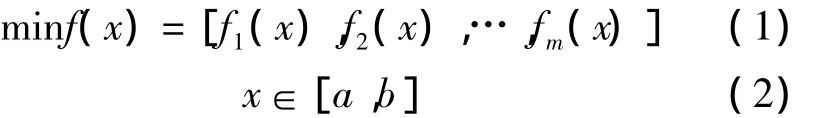
式中:目标函数f(x)∈Rm;决策向量x∈Rn，即x=(x1，x2，…，xn)。

这里给出的是极小化问题，对于极大化问题与上述形式类似。为了比较多目标优化问题的解，下面给出Pareto最优解的定义。

如果不存在 y∈[a，b]使 fi(y)≤fi(x)(i=1，2，…，m)，且至少有1 个不等式成立，则 x∈[a，b]是多目标优化问题的Pareto最优解。由该定义可知，Pareto最优解集中的解彼此是不可比较的，解集分布越广泛，解的数量越多，越能合理求解实际的多目标问题。

多目标优化遗传算法很多，本文主要采用Deb于2000年提出的多目标优化遗传算法NSGA－Ⅱ[6－7]。

2 压裂水平井裂缝参数优化设计多目标遗传算法

2.1 采出程度－含水率二维多目标优化模型建立

在低渗透油藏压裂水平井注水开发中，裂缝条数、裂缝半长、裂缝间距、裂缝与水平井筒间夹角、裂缝导流能力等参数对压裂水平井的采出程度和含水率都会产生显著的影响。为了研究各个裂缝参数的最佳取值范围，需要选取待优化的目标函数。油田生产中为了效益最大化，往往是采出程度越大越好，在采出程度相同的情况下，含水率越低越好。但是这2个目标函数又是相互冲突的，往往采出程度高时含水率也很高，为了能在获取较高采收程度的同时控制含水率的快速上升，需要对压裂水平井裂缝参数进行优化。

待优化的2个目标函数为采出程度η和含水率fw，为了统一研究目标函数的最大化问题，取fo=1－fw，待优化的目标函数变为:

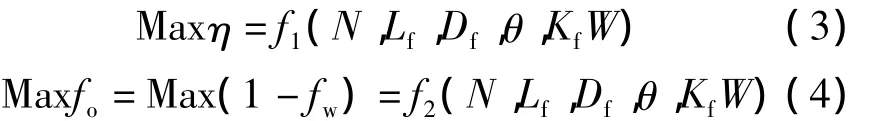
式中:N为裂缝条数;Lf为裂缝半长，m;Df为裂缝间距，m;θ为裂缝与水平井筒间夹角，(°);KfW为裂缝导流能力，μm2·cm;fo为含油率。

2.2 适应度计算

个体适应度由Pareto等级和拥挤距离共同决定，每个个体所对应的是优先级，不是确定的适应度值。

(1)Pareto等级。先通过编制的软件求出种群中每个个体的目标函数值。再通过非支配分类法确定个体的非支配等级即Pareto等级。对于1个解i，其Pareto等级ri等于1加上优于其解的个数ni，即ri=ni+1。所有非支配最优解构成了第1个非支配最优解层，该层个体的Pareto等级为1，然后以相同的方法对种群中剩下的个体进行排序，直至种群中的个体都被归类完毕(level=2，3，…)。

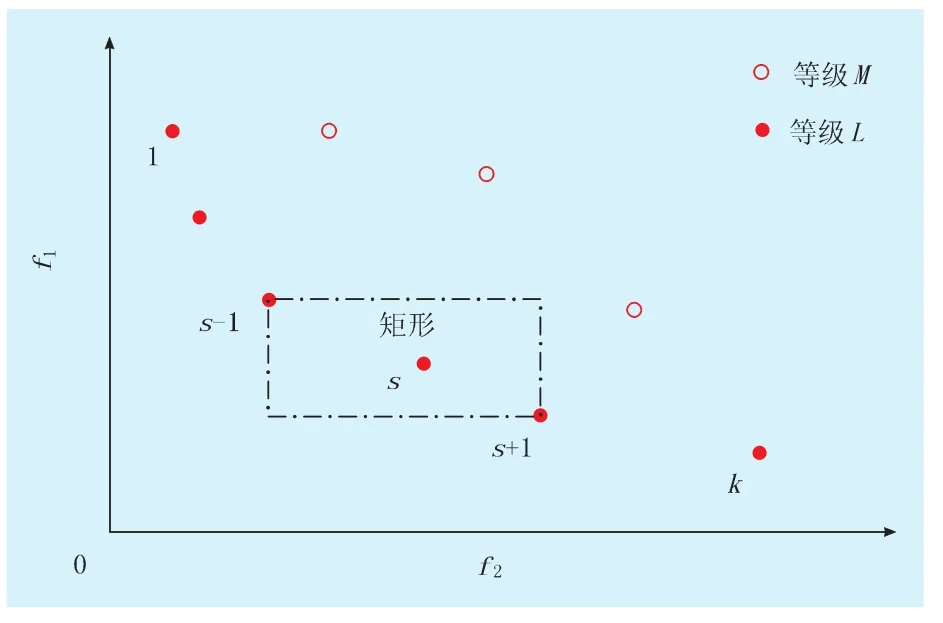
图1 二维多目标优化中个体拥挤距离示意图

(2)拥挤距离。拥挤距离用来表征非劣解中解的多样性，拥挤距离指目标空间上某一点与其同等级相邻的2点在各目标函数上相对距离之和(图1)。如图中实心圆点代表等级L，空心圆点代表等级M。以等级L为例，各点拥挤距离的算法如下:①等级L中个体的拥挤距离初始化为L[s]dis(s=1，2，…，k，其中，s代表第 s个个体，k 代表等级 L中个体数目);②同等级的个体，根据第p目标函数值的大小升序排列，令L=sort(L，p);③对边缘上的个体1和k都赋予1个极大值;④对于中间的个体(s=2，…，k－1)，拥挤距离计算式为:

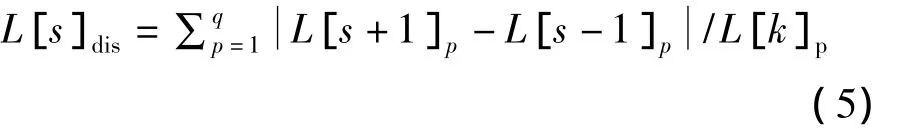
式中:L[s+1]p为第s+1个个体的第p个目标函数值;L[s－1]p为第s－1个个体的第p个目标函数值;q表示目标函数值的个数。

2.3 个体选择

在进行压裂水平井裂缝参数优化设计过程中，需要按目标函数(即适应度)的大小对父代中的个体进行排序，从小到大编排序号(1，2，3，…i，…N)，则个体 i的概率区间为，其中:，这样既能体现优胜劣汰法则，同时又兼顾了个体的多样性。

2.4 交叉系数和变异系数的优选

交叉和变异操作是多目标遗传算法的核心，决定着新个体的产生。交叉系数和变异系数的取值有一定的范围，一般情况交叉系数变化范围为0.40～0.99，变异系数变化范围为0.0001 ～0.1000[8]。利用该算法对研究区块某注水开发压裂水平井裂缝参数进行优化设计，直井注水，水平井采油。从表1中可以看出，循环代数越多，算法优化效果越好，而采用适中的交叉系数0.65和变异系数0.0050有利于优化设计[9－12]。

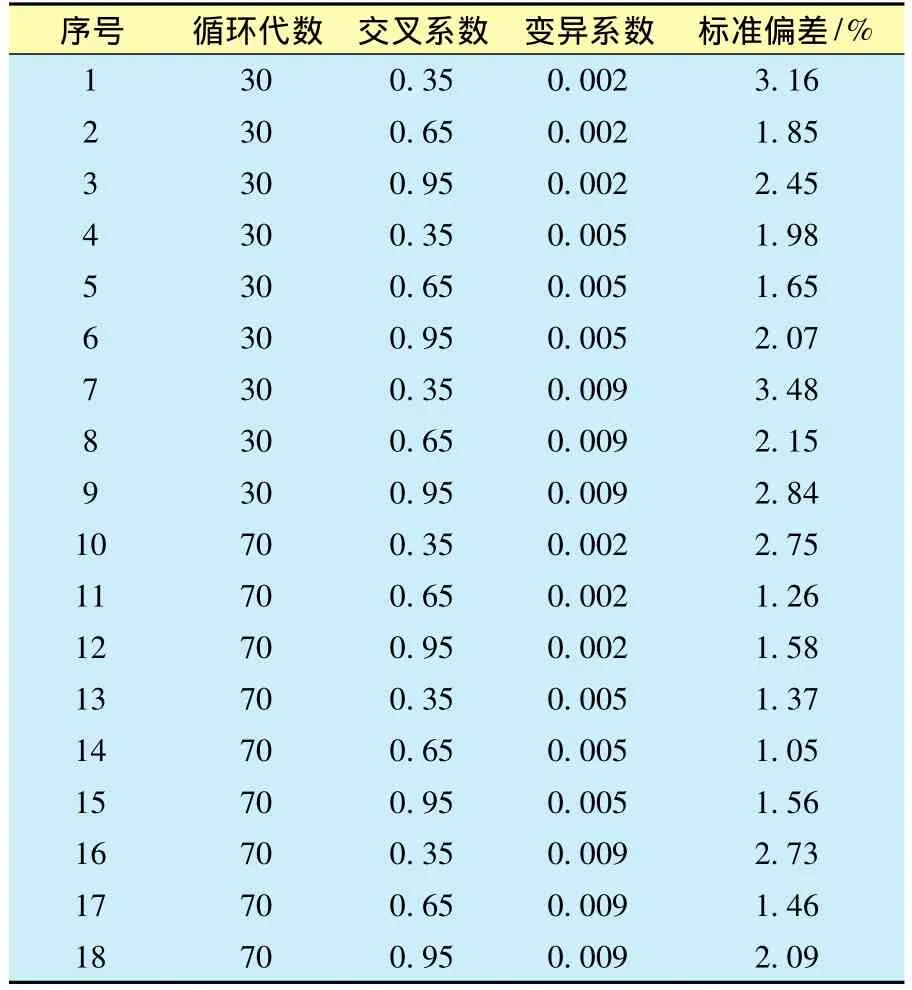
表1 不同遗传组合的标准偏差

2.5 多目标遗传算法优化步骤

根据多目标优化遗传算法的规则，按照图2所示优化步骤对低渗透油藏压裂水平井裂缝参数进行优化设计。当达到最大进化代数且所得Pareto最优解集具有良好的收敛性和多样性时，所得的参数组合就是最佳裂缝参数组合。应用Visual Basic软件编制的多目标优化遗传算法计算程序，可实现数模软件自动运算和数据图表自动显示功能，降低人工工作量，且该算法受优化对象数目的影响小。

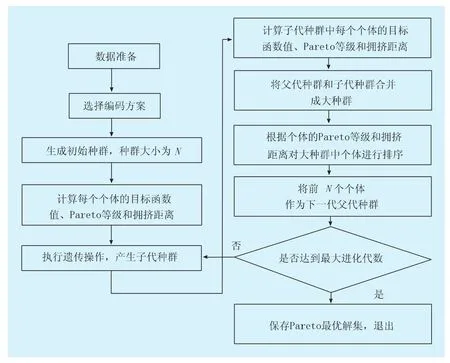
图2 多目标遗传算法优化流程示意图

3 实例计算

根据研究区块实际地质资料以七点法直井－水平井组合井网压裂水平井为研究对象。基本假设:①人工裂缝垂直于水平井井筒且延伸方向不存在偏转;②不考虑裂缝时效性对产能造成的影响。

该油藏相关数据如下:油层顶深为2250 m，地层平均绝对渗透率为0.306×10－3μm2，渗透率各向异性取值:Kx=2Ky，Ky=3Kz，平均孔隙度为12%，属于典型的低孔、特低渗储层。原始油藏压力为18.5 MPa，地层平均有效厚度为10 m，原始含油饱和度为80%，地层原油黏度为1.415 mPa·s，原油密度为0.852 g/cm3，原油体积系数为1.15，原油压缩系数为12.56×10－4MPa－1。直井注水，压裂水平井采油，井距为650 m，排距为300 m，水平井段长度为1000 m(图3)。以生产25 a之后的采出程度和含水率为目标函数进行优化设计，各裂缝参数优化情况如表2所示。

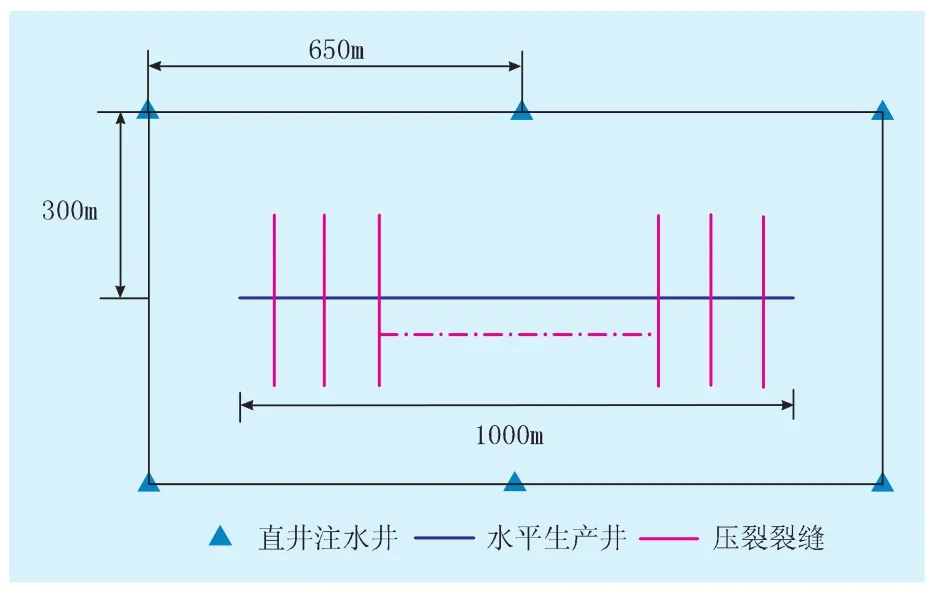
图3 七点法直井－水平井混合压裂井网示意图

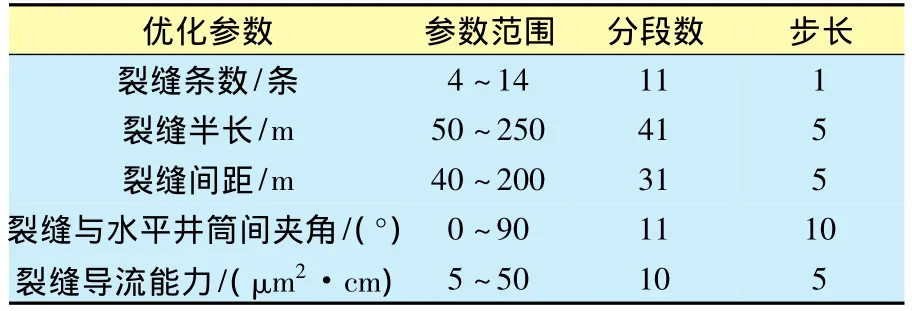
表2 裂缝优化参数

以定井底流压方式生产，保持注采压差为20 MPa。理论上待优化的个体有1537910(11×41×31×11×10)个，如果采用枚举法，软件运行时间将会非常长，在实际中是很难实现。利用多目标遗传算法NSGA－Ⅱ进行优化时，种群规模取40，当交叉概率为0.65，变异概率为0.0050，循环代数为55代时，能得出Pareto最优解集。对实例随机运行15次，这15次运行得到的Pareto最优解集的分布区域是相同的。图4为实例第1次运行的结果，散点为软件运行结果。由图4可知，所得最优解集在Pareto前沿分布均匀，具有良好的多样性和收敛性。利用多目标遗传算法优化出的结果为:裂缝条数为8～10条、裂缝半长为120～150 m、裂缝间距为100～150 m、裂缝与水平井筒间夹角为90°、裂缝导流能力为25～35 μm2·cm的参数组合时，能达到最佳生产效果。

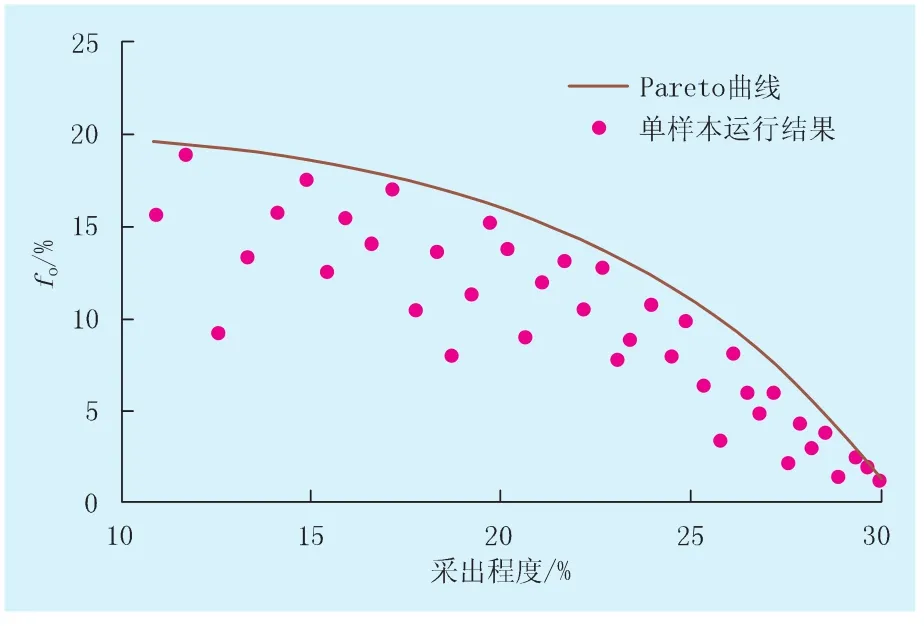
图4 实例分析Pareto曲线与软件优化

采用多目标遗传算法优化设计的结果和常规优化方法基本一致，但是比专家系统法和模糊数学法扩展了搜索空间，相比枚举法提高了优化速度，适用优势明显。

4 结论

(1)提出了应用多目标优化遗传算法对低渗透油藏注水开发压裂水平井裂缝条数、裂缝半长、裂缝间距、裂缝与水平井筒间夹角和裂缝导流能力进行优化设计的新方案。

(2)引入Pareto最优解集概念，将采出程度和含水率作为2个目标函数，利用开发软件结合多目标遗传算法NSGA－Ⅱ对裂缝参数进行优化设计。该方法新颖可靠，所需资料较少，运算快捷。

(3)多目标优化遗传算法在搜索过程从种群参数成员(一般由多个个体构成)开始，搜索效率更高，当所求解的问题为非连续、多峰等情况，能以较大概率收敛到最优解，具有较好寻优能力。

[1]杨正明，黄延章，朱维耀.水平井开发低渗透油藏渗流特征[J].特种油气藏，1999，6(2):16－20.

[2]柳毓松，廉培庆，同登科.利用遗传算法进行水平井水平段长度优化设计[J].石油学报，2008，29(2):296－299.

[3]胡文瑞.水平井油藏工程设计[M].北京:石油工业出版社，2008:150－159.

[4]李敏强，寇纪淞，林丹，等.遗传算法的基本原理与应用[M].北京:科学出版社，2003:126－132.

[5]祁荣宾，钱锋，杜文莉，等.基于精英选择和个体迁移的多目标遗传算法[J].控制与决策，2007，22(2):164－168.

[6]王健，刘尔烈，骆刚.工程项目管理中工期－成本－质量综合均衡优化[J].系统工程学报，2004，19(2):148－153.

[7]Deb K，Pratap A，Agarwal S，et al.A fast and elitist multiobjective genetic algorithm:NSGA － Ⅱ[J].IEEE Transactions on Evolutionary Computation，2002，6(2):182－197.

[8]宋万道，张凤喜，安永生，等.压裂水平井井网参数自动优化研究[J].特种油气藏，2009，16(4):101－103.

[9]黄辉，吴晓东，孙天礼.基于遗传算法的低渗透气藏水平井压裂参数优化[J].天然气工业，2008，28(5):91－93.

[10]Daniel P Fichter，Merak Projects inc.Application of genetic algorithms in portfolio optimization for the oil and gas industry[C].SPE62970，2000:265 －276.

[11]郑黎明，蒲春生.压裂水平井增产因素分析与裂缝参数优化[J].大庆石油地质与开发，2012，31(6):109－113.

[12]曲占庆，赵英杰，温庆志，等.水平井整体压裂裂缝参数优化设计[J].油气地质与采收率，2012，19(4):106－110.