基于双谱和希尔伯特-黄变换的断路器故障诊断方法

李建鹏，赵书涛，夏燕青

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

断路器的正常运行对电网的稳定、安全运行至关重要。目前实行的计划性预防检修盲目性大，而且频繁的操作及过度的拆卸检修会降低断路器的可靠性。断路器在开、闭操作过程中会发出巨大的声响和振动，这种声波和振动信号是断路器运行状态信息的重要载体。声波可由非接触测量方法获得，适合应用在高电压和强电磁环境中［1］。声波中包含了断路器运行隐患和故障信息，声波分析虽然具有易于测量的优点，但测试环境中的各种干扰同时会影响声波分析结果。处理线性、高斯性和平稳性信号时，可采用二阶统计量或基于二阶统计量的功率谱理论分析信号的时频域特征。但是断路器的声波信号易受环境因素影响，且包含非线性、非平稳成分，此时再采用常规的处理方法会大幅降低准确性，甚至产生错误的结论。

双谱从更高阶概率结构表征随机信号，理论上能够完全抑制高斯噪声，适用于分析非线性、非平稳信号［2］。希尔伯特-黄变换 HHT（Hilbert-Huang Transform）经过经验模态分解EMD（Empirical Mode Decomposition）把信号分解成若干个固有模态函数IMF（Intrinsic Mode Function），然后对 IMF 进行 Hilbert变换，得到每个IMF的随时间变化的瞬时频率和瞬时幅值，由此可构建信号的时间-频率-能量分布。将双谱分析和基于EMD的能量熵用于非线性、非平稳的声波信号分析，对于诊断断路器运行状态是一种有益的探索。

1 断路器操动过程中的声波信号

由于机械的撞击和摩擦，断路器在分、合闸过程中发出的声波中蕴含了丰富的机械状态信息。声波传感器的安装相对灵活简便，不需改变设备结构，所以与其他检测法相比，声学检测具有简单灵活、易于在线检测的优点［3］，但获得的声波信号中常含有大量噪声，严重影响了信号处理结果。采用电容型传声器采集断路器合闸的声波信号，采样频率为10 000 Hz，采样点为30000个，如图1所示（声波信号已转换为电压信号，后同）。从图1可以看出，断路器合闸声波信号在1.0 s左右振幅最大，进一步分析信号的功率谱，如图2所示。由图2可以发现合闸声波信号能量主要分布在0～3000 Hz，3000 Hz以上信号能量很小。基于傅里叶变换的功率谱分析是对信号的全局积分，不能反映信号的局部频域特征。而声波信号频率分布的时间特性和断路器机械状态密切相关，通过功率谱不能反映声波信号频率的时间特征，也就不能直接诊断断路器故障。

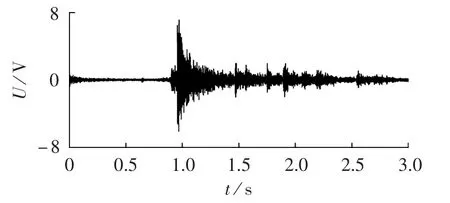
图1 断路器合闸声波信号Fig.1 Acoustic signal of circuit breaker closing

图2 合闸声波信号功率谱Fig.2 Power spectrum of closing acoustic signal

为考虑环境噪声影响，采集断路器周围环境噪声信号（断路器未动作时），通过比较来确定噪声的影响。图3为环境噪声信号时域波形图，信号幅值很低。图3的功率谱分析如图4所示，噪声能量集中在 500 Hz以下，500 Hz以上信号能量极小。可见，500 Hz以下噪声会对断路器状态特征的提取产生影响。

图3 环境噪声信号Fig.3 Environmental noise

图4 环境噪声功率谱图Fig.4 Power spectrum of environmental noise

当断路器操动中存在故障隐患时，声波信号会有显著变化，然而直接通过人的听觉尚不能区分故障及其类型，找到合适的诊断断路器运行状态的声波处理方法具有重要的实用价值。

2 双谱分析

作为信号处理的重要方法之一，双谱分析从更高阶概率结构表征随机信号，可以弥补功率谱不含相位信息、无法提供更多有用信息的缺点。同时，双谱分析理论上能够完全抑制高斯噪声，具有很强的消噪能力。因此，双谱分析在非平稳、非高斯信号的时延估计、去噪处理和特征提取方面应用非常广泛。双谱的定义如下。

假设｛x（n）｝为零均值的k阶平稳随机过程，并且其k阶累积量Ck，x（τ1，τ2，…，τk-1）是绝对可和的，即：

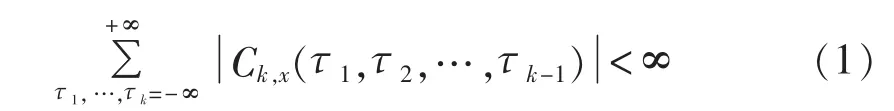
则｛x（n）｝的k阶谱定义为：

其中，k=3时为双谱，即：

基于双谱分析的优良特性，将双谱分析应用到断路器声波信号的分析和处理中，以获得更多的有用信息。断路器在灭弧室动触头、机械连接机构等动作时，其动作过程往往表现为非平稳、非线性［4］。对于非线性系统而言，在某些频率处会出现较强的相关性，表现为在双频率坐标下的双谱分析三维图上出现较高的谱峰。

图5为正常状态合闸声波信号双谱分析三维图，图6为缓冲器有多余无效撞击时合闸声波信号双谱分析三维图，图7为合闸弹簧储能不足时合闸声波信号双谱分析三维图。对比图5、6、7可以发现，双谱幅值存在，不为0，说明合闸声波信号存在非线性、非高斯特性。正常状态时，合闸声波信号三维谱图分布比较规律，表现为1个能量较大的主谱峰周围围绕6个能量较小的谱峰；出现故障后，主谱峰幅值减小，小谱峰个数增多，分布变得杂乱，能量趋于发散。观察双谱分析平面图8—10（f1、f2已作归一化处理，基准频率为10000 Hz），同样可以发现，出现故障后，能量分布变得复杂、分散，6个小谱峰周围也出现很多谱峰，谱图发生很大变化。可见，声波信号中非线性、非高斯成分能量分布的变化在一定程度上表征了断路器机械状态的变化。

图5 正常状态合闸声波信号双谱分析三维图Fig.5 Three dimensional figure of bispectrum analysis for normal closing acoustic signal

图6 缓冲器有多余无效撞击时合闸声波双谱分析三维图Fig.6 Three dimensional figure of bispectrum analysis for closing acoustic signal when buffer has extra invalid hit

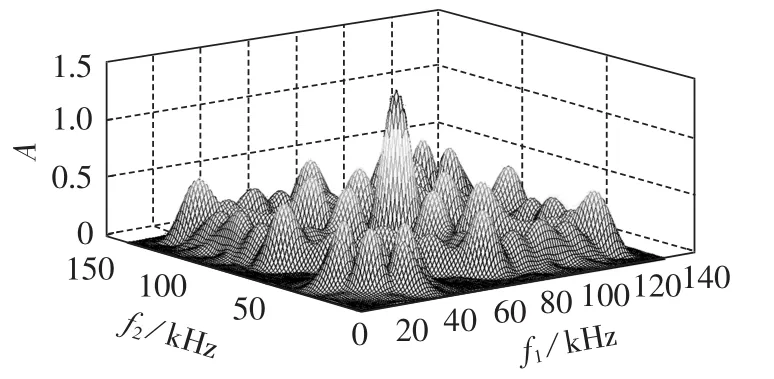
图7 合闸弹簧储能不足时合闸声波双谱分析三维图Fig.7 Three dimensional figure of bispectrum analysis for closing acoustic signal when closing spring has less energy storage

目前断路器机械状态识别的研究表明，断路器的机械状态与特征向量之间存在复杂的非线性映射关系。对于相同或相似的机械状态，声波信号双谱的非线性特征相似；对于不同的机械状态，其双谱中体现的非线性特征也不相同，具有较强的可分性［5-7］。断路器存在隐患或发生故障时，其声波信号各个频率成分的能量中包含着丰富的故障信息，某种或几种频率成分能量的改变即代表了某种故障。因此，双谱分析在断路器状态识别中有着良好的应用前景。

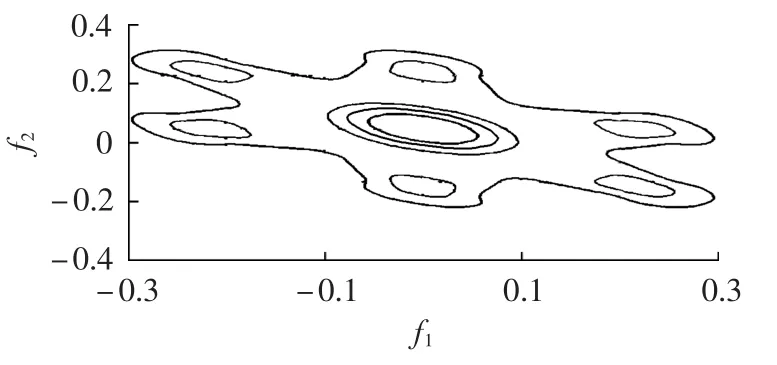
图8 正常状态合闸声波信号双谱分析平面图Fig.8 Plan of bispectrum analysis for normal closing acoustic signal

图9 缓冲器有多余无效撞击时合闸声波双谱分析平面图Fig.9 Plan of bispectrum analysis for closing acoustic signal when buffer has extra invalid hit

图10 合闸弹簧储能不足时合闸声波双谱分析平面图Fig.10 Plan of bispectrum analysis for closing acoustic signal when closing spring has less energy storage

3 HHT分析

HHT主要包括EMD和Hilbert变换两部分。

EMD方法的本质是通过数据的特征时间尺度来分离固有波动模式，即IMF的过程。基于任何复杂的信号都是由一些不同的IMF组成的假设，对复杂信号进行“筛分”，使复杂信号经Hilbert变换后的瞬时频率具有物理意义［8］。

EMD具体步骤如下。

a.找到信号x（t）所有的局部极大值点和局部极小值点，然后利用三次样条差值函数拟合形成原始数据的上、下包络线 s1、s2。

b.将上、下包络线的均值记作m1，求出：

判断h1是否满足IMF成立的2个条件，即：极值点个数和过零点个数相等或最多相差1个；在任意时刻，由局部极大值点和局部极小值点形成的上、下包络线平均值为0。如果满足，那么h1就是x（t）的第1个IMF分量。

c.如果h1不满足IMF的条件，把h1作为原始数据，转步骤a。

d.得到h1上、下包络线的平均值m11，再求出：

判断h11是否满足IMF成立的条件，如不满足，则重循环k次，得到：

最终使得h1k满足IMF的条件。从滤波的角度看，h1k为h1（k-1）中的局部高频分量，m1k代表了局部低频分量；记 c1=h1k，则 c1为信号 x（t）第 1 个满足 IMF 条件的分量。

e.将 c1从 x（t）分离出来，得到：

其中，r1为原始数据减去第1个IMF分量的剩余序列。将r1看作原始数据重复步骤a—c得到第2个IMF分量，重复循环n次，得到x（t）的n个满足IMF条件的分量。这样就有：

当rn成为一个单调函数不能再从中提取满足IMF条件的分量时，循环结束。这样由式（7）和式（8）得到：

其中，rn为残余函数，代表信号的平均趋势；n为筛选出的IMF分量个数。

f.对每个IMF分量作Hilbert变换：

其中，p为联合概率密度函数。

定义瞬时频率为：

以上EMD和与之相应的Hilbert变换分析方法统称为HHT。

图11和图12分别为某断路器合闸声波信号和环境噪声的HHT分析，频率已作归一化处理。对比两图可以看出，低频（500 Hz以下）分量在整个合闸过程存在，500～3000 Hz信号主要集中在1.0 s左右，持续时间约为400 ms，携带了丰富的断路器状态信息，高频（3000 Hz以上）分量能量极小。此时，提取500～3000 Hz频段内声波信号作为特征信号进行后续分析，可以在最大限度地保留有用信号的情况下去除低频环境噪声干扰。

图11 合闸声波信号希尔伯特-黄谱Fig.11 Hilbert-Huang spectrum of closing acoustic signal

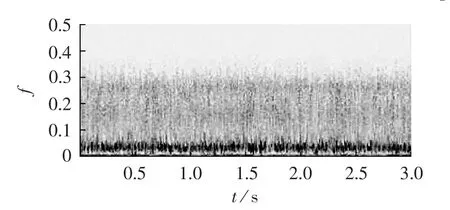
图12 环境噪声信号希尔伯特-黄谱Fig.12 Hilbert-Huang spectrum of environmental noise

4 提取故障特征

EMD 的分解结果，即c1（t）、c2（t）、c3（t）、…，分别反映信号中内嵌的简单函数振荡模式，它们依次包含从高频到低频的信号频率成分，是信号频带的一种自动划分，随信号本身的变化而变化［9-10］。所以，笔者将提取合闸声波信号特征频段（500～3000 Hz）内信号的IMF能量熵作为故障诊断特征向量，基于IMF能量熵的特征提取步骤如下。

a.对合闸声波信号特征频段内信号进行EMD，选取包含断路器主要故障信息的前n个IMF分量。

b.求各IMF分量的能量Ei：

c.以各IMF能量为元素构造总能量E：

d.IMF能量熵定义为：

其中，pi=Ei/E，为第i个IMF分量的能量占整个信号能量的百分比。断路器状态变化引起声波信号能量分布发生变化，熵值随之变化。根据熵理论，按照步骤a—d得到的能量熵能够反映各个IMF分量能量的分布情况。

5 实验分析

在实验室中采集LW3-12型SF6断路器正常、合闸弹簧储能不足、缓冲器有多余无效撞击3种状态下各10组合闸声波数据。根据第4节所述的故障特征提取方法，计算得到的各种状态下的IMF能量熵如表1所示。其中，1为正常状态，2为合闸弹簧储能不足状态，3为缓冲器有多余无效撞击状态。

表1 IMF能量熵Tab.1 Energy entropy of intrinsic mode function

断路器运行环境复杂，声波信号采集过程中常受到背景噪声干扰，会对信号分析结果产生影响。因此，先对各状态IMF能量熵进行聚类分析，再诊断断路器运行状态。图13为在最短距离规则下正常状态能量熵的聚类过程，1～10分别代表由低到高10个固有模态能量熵。剔除2个相异性最大的数据，计算剩余8个相似性较好数据的平均值，以此作为能量熵中心值。合闸弹簧储能不足、缓冲器有多余无效撞击等状态下同样进行聚类处理，剔除2个最坏的数据，保证了处理结果的冗余度。例如在正常状态下能量熵1.2153单独一类，相异性最大，已经被剔除，此外还剔除了能量熵1.2086。合闸弹簧储能不足状态下剔除1.291 7和1.337 4这2个能量熵。缓冲器有多余无效撞击状态下剔除1.2301和1.0524这2个能量熵。

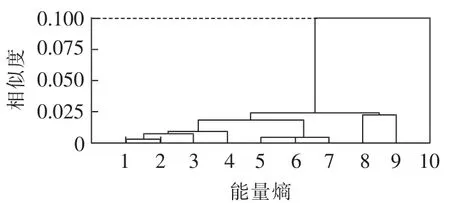
图13 正常状态能量熵聚类分析Fig.13 Clustering analysis of energy entropy for normal state

计算得到各状态能量熵中心值如表1所示。以能量熵中心值为标准，计算每次测试数据能量熵到各状态中心值的距离，根据距离接近程度诊断断路器故障类型。在实验室中对LW3-12型SF6断路器的上述3种状态进行了多次测试，均能准确区分。断路器其他类型故障也可采用本文提出的方法计算能量熵中心值，将此中心值作为标准放入知识库，通过专家系统有效地诊断断路器故障。

6 结论

断路器操动中的声波信号能体现断路器的运行状况。利用双谱分析了断路器合闸声波的能量分布特性，表明机械故障可由500～3000 Hz范围内声波信号区分。利用HHT分析了合闸声波的时频分布特性，将IMF能量熵经聚类分析，求取中心值诊断断路器故障类型，是一种实用的新方法。断路器故障诊断十分复杂，声波分析法在工程实际中还需要更多的现场数据充实知识库中的评价标准，并结合神经网络、模糊理论和专家系统等进一步展开研究工作。