高压大功率E型变压器漏感有限元仿真计算

王亚超，刘 军，何湘宁

（浙江大学 电力电子技术国家专业实验室，浙江 杭州 310027）

0 引言

高压大功率变压器是谐振式高压静电除尘电源的关键部件，其漏感作为谐振电感参与电路工作，直接决定电路的拓扑和控制方式，因此要求变压器设计时，能够对漏感进行较为准确的计算［1］。

变压器的漏感主要受磁芯和绕组结构、制作工艺及工作频率的影响，其中工作频率的影响主要表现为高频下的涡流效应，在低频时可忽略［2］。绕组同心柱绕制的E型磁芯变压器（以下简称E型变压器），其漏感可利用与变压器结构参数有关的一维解析式计算［3］，或利用改造后的二维有限元轴对称模型仿真［4］。原副边绕组非同心柱结构的E型变压器，其漏感的一维解析式较复杂，特殊情况下，如绕组紧密围绕磁芯绕制时，可选择双二维有限元模型仿真［5-6］。三维有限元模型在正确建模和剖分的基础上，可得到精确性较高的仿真结果，与二维有限元模型相比，其有限元网格剖分复杂，仿真时间长，对计算机内存和存储器的要求也更高。尤其对于尺寸大、匝数多和绕组结构较为复杂的高压高频大功率变压器，综合考虑建模过程、仿真精度和仿真时间等因素，目前采用二维有限元仿真模型可达到缩短仿真时间、降低仿真难度的目的［4-7］。

本文以一个输出72 kV/1 A的高频电除尘电源为例，计算应用于该变换器的E型变压器的漏感。该变压器无气隙，原副边绕组同心柱绕制，不考虑涡流效应时，其漏感可用一维解析式计算［3］，但该方法对漏磁分布作了较多的简化和等效，计算精度不高。考虑涡流效应后，虽然可使用数值法对漏感进行理论计算，但应用复杂，且只在某些特殊结构下具有较好的计算精度［8-11］。有限元仿真可准确方便地模拟真实磁场分布，但E型变压器为非轴对称结构，不能直接应用二维轴对称模型，且该变压器副边绕制在与磁芯距离较大的圆形骨架上，也不适用双二维模型。鉴于变压器的结构复杂、尺寸较大，选择适当的二维有限元模型，在满足较高的仿真精度前提下，缩短仿真时间，是较好的选择。

对于无气隙E型变压器，文献［4］基于阻抗相等的概念，通过对磁芯磁导率和导体电阻率进行改造，使仿真模型阻抗与实际变压器阻抗相等，提出了适用于E型变压器仿真的二维轴对称模型，但由于只考虑了一个截面，在等效三维磁场分布上还存在一定缺陷。文献［7］继承文献［4］磁阻相等的理念，由2个不同截面轴对称模型的组合，形成了更接近E型变压器磁场分布的二维轴对称模型，称之为二维ERXP模型。

本文分析的变压器原副边绕组均绕制在磁芯中柱上，且中柱截面为矩形，但文献［7］仅对中柱截面为圆形的E型变压器进行了研究。因此，结合实际变压器的结构和文献［4］对矩形截面的等效，文中对二维ERXP模型进行了合理的改造，得到了适用于该类型变压器的漏感仿真模型。

1 应用背景及漏感计算方法概述

1.1 LCC高压静电除尘电源简介

本文分析的变压器应用在高压大功率LCC谐振变换器上，其电路拓扑如图1所示，输入为直流500 V电压，额定输出为72 kV/1 A。虚线框所示为变压器的简化模型，其漏感Lr和绕组电容Cp作为谐振元件，与外加的串联谐振电容Cr一起组成了LCC谐振。

图1 LCC谐振变换器电路拓扑Fig.1 Topology of LCC resonant converter

谐振电流ir简化波形如图2所示，其中，第1、2幅图分别为VT1、VT4和 VT2、VT3的开通及关断脉冲。通过对电路的分析可知，漏感Lr直接影响电路的调频调压特性和谐振电流峰值，因此，在设计变压器时，进行准确的漏感计算，对谐振变换器功率器件的选取以及电路的优化设计具有指导意义。

图2 谐振电流典型波形Fig.2 Typical waveform of resonant current

1.2 漏感一维解析算法

变压器漏感一维解析算法，不考虑高频涡流效应，认为磁力线在磁芯窗口一维分布，直接利用变压器结构参数计算［3］。本文分析的变压器初、次级绕组均安放在中柱上，低压绕组为6匝300 mm×0.2 mm铜箔，高压绕组采用1.12 mm漆包线，分别缠绕在12个槽内，每个槽分9层。变压器结构和线圈窗口磁场分布如图3所示，由于应用在高压场合，原副边留有足够大的绝缘距离以保证线圈不被击穿，绕组间的漏磁场能量较大。

图3 变压器绕组结构及窗口磁场分布（正视图）Fig.3 Transformer winding structure and magnetic field distribution in core window（front view）

变压器的漏感是一个寄生参数，用来表征漏磁通所产生的磁场能量，假定磁场强度H在磁芯窗口线性变化，如图3所示，则总磁场能量Wm可通过对磁场强度H的线性积分求得，等效到初级侧的变压器漏感Lr计算公式为：

其中，I1为变压器原边电流；N1为变压器原边绕组匝数；μ0为空气磁导率；le为磁芯窗口高度；b为原边绕组宽度；d为副边绕组宽度；lav1、lav2为原边、副边绕组平均匝长；S为原副边间隔带的上视面截面积。

一维解析算法忽略了磁芯中的漏磁通，认为磁芯中的磁场强度为零，磁芯窗口的磁场能量即等于总的漏磁能量；不考虑涡流效应，认为磁场在磁芯窗口一维分布，磁场强度在原副边绕组间保持不变。但实际变压器的磁芯相对磁导率不是无穷大，磁芯中的漏磁通会产生少量的漏磁能量，且原边和副边绕组高度均小于磁芯窗口高度，在绕组端部的磁场分布会发生畸变，原副边绕组间磁场强度也非定值，因此，一维解析算法并不适用于漏感的精确计算。

1.3 E型变压器二维有限元仿真模型比较

已有文献提出了几种适用于E型变压器的二维仿真模型，在电磁场仿真方面达到了较小的计算误差［8-11］。鉴于本文分析的变压器三维结构复杂，导致三维有限元剖分难度较高且仿真时间较长，因此，在综合考虑仿真时间和仿真精度的前提下，通过对几种现有的二维模型进行比较，选择了二维ERXP轴对称模型。

二维轴对称模型适用于轴对称结构的变压器，基本思想是建立一个变压器的1/2模型截面，通过绕对称轴旋转形成实体，以等效实际的三维结构。文献［4］基于阻抗相等的概念，在平行于磁芯最长边的截面（以下简称P截面，如图4所示）建立了改造的1/2轴对称模型，但由图4可见，该模型也存在缺陷，未考虑垂直于磁芯最长边的截面（以下简称T截面），而T截面磁场分布显然不同于P截面。

图4 E型变压器P截面和T截面Fig.4 P and T sections of E-core transformer

文献［5-6］提出的双二维模型在P截面和T截面分别建立平面模型，忽略绕组拐角处的能量，仿真结果分别乘以绕组在该平面的延伸长度，相加后等效实际E型变压器的三维磁场分布。该模型适用于绕组紧密围绕磁芯柱的E型变压器，本文分析的E型变压器应用在高压场合，原副边有很大的绝缘距离，副边绕组绕制在距离磁芯较远的圆形骨架上，所以该方法并不适合。

文献［7］提出了一种称为ERXP的二维轴对称模型，该模型结合了文献［4-6］的优势，基于磁阻相等的建模思想，分别在P截面和T截面建立轴对称模型，P截面建立ER模型，T截面建立XP模型。对模型的结构参数进行了改造，使2个模型的等效磁阻与实际变压器磁阻保持一致，并在XP模型中增加了一个额外的磁芯柱，构成低磁阻磁通流通路径，以更好地模拟E型变压器的三维电磁场分布。

通过以上比较可见，二维ERXP模型理论上比其他二维模型更适用于E型变压器的仿真。文献［7］仅讨论了磁芯中柱为圆形截面的情况，本文分析的变压器磁芯中柱为矩形截面，下文结合实际变压器的结构和文献［7］对矩形截面的等效，建立了适用于磁芯中柱为矩形截面的ERXP模型，文中所使用的ERXP模型基本公式均参考文献［7］。

2 ERXP模型漏感计算

2.1 加权平均系数及实际变压器磁阻求解

ERXP模型包括P和T 2个轴对称的截面，2个模型的仿真结果经过加权平均后，等效实际变压器的三维磁场分布。根据ER和XP模型各自对应的绕组上视面截面积，决定加权平均系数。本文分析的变压器，原边绕组为紧密绕在磁芯中柱的铜箔，其上视面截面积相对副边很小，对加权平均系数影响不大，故不予考虑，只根据副边绕组上视面截面积来计算加权平均系数。实际变压器的上视图如图5所示，A1为XP模型对应的副边绕组截面，A2为ER模型对应的副边绕组截面，加权系数η可由式（2）求得，ER和XP模型仿真结果加权平均后得到总仿真结果如式（3）所示。

其中，WERXP、WXP、WER分别为总仿真结果、XP 模型仿真结果和ER模型仿真结果。

为建立ERXP模型，首先要求出实际变压器的总磁阻，E型变压器1/2模型的等效磁阻计算模型如图6所示。

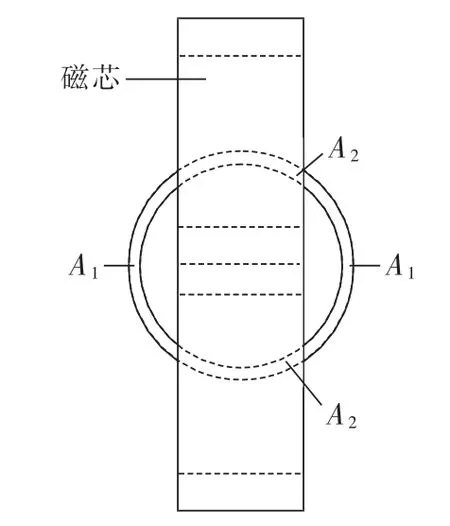
图5 变压器上视图Fig.5 Top view of transformer

图6 变压器磁阻计算模型Fig.6 Calculation model of transformer magnetic reluctance

根据图6所示磁力线的流通路径可得到1/2变压器的等效磁阻模型，其中，磁阻 R1、R2、R3、R4可由式（4）求得，窗口磁阻Rw与磁芯磁阻2R3+R4并联，可由式（5）求出，变压器的总磁阻根据各等效磁阻的连接方式可由式（6）求出。

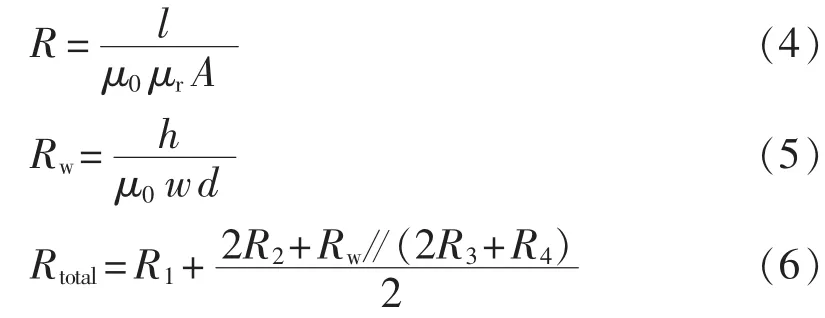
其中，μ0为空气磁导率，μr为磁芯的相对磁导率，l为磁通流通方向上的长度，A为截面积。

2.2 建立ERXP模型

实际变压器磁芯中柱为矩形截面，在保证磁芯中柱磁阻R1不变的前提下，为建立二维ERXP模型，将矩形截面等效为等面积的圆形截面，则紧密绕在磁芯中柱的原边绕组周长会改变，为不影响仿真效果，根据式（7）改变原边导体的电阻率，使原边导体电阻保持不变［4］。

其中，ρm为ERXP模型导体等效电阻率，ρcu为实际铜导体电阻率；la为原边绕组的实际周长，lm为ERXP模型的原边绕组周长。

ERXP模型磁芯中柱磁阻经过上述等效后，与实际变压器磁芯中柱磁阻R1保持一致。ER二维轴对称模型在P截面建立，要保证总磁阻相同，仅需改变P截面中E型磁芯的所有边柱尺寸为t，磁芯窗口尺寸保持不变，如图7所示。

图7 ER模型Fig.7 ER model

ER模型根据磁通流通路径等效的磁阻模型如图 7（c）所示，ER 模型总磁阻 RER可由 R1、Rtop、Router和Rw根据其连接方式由式（8）求得，各磁阻计算公式见式（9）—（11），式中所有尺寸标注见图 7（b），其中O表示以对称轴为起点，ri、rave、ro为从起点到相应点距离的尺寸标注。保持磁芯中柱磁阻R1不变，仅改变边柱尺寸为t，使该模型总磁阻RER与实际变压器总磁阻Rtotal相等，解出唯一的未知尺寸t，即可建立ER模型。

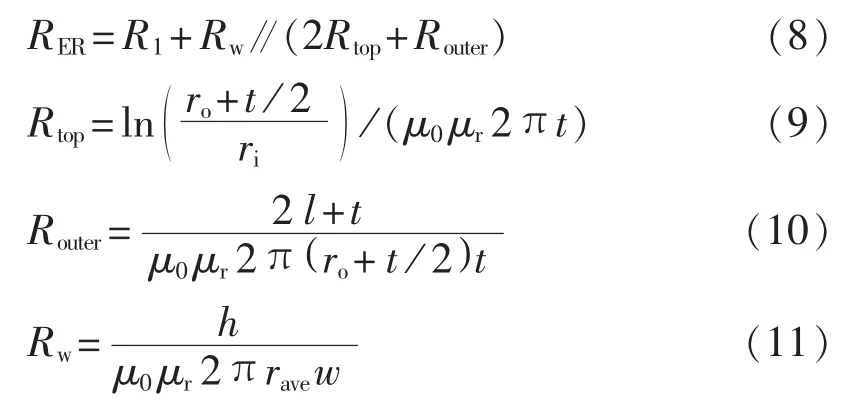
XP二维轴对称模型在T截面建立，实际变压器T截面如图8（a）所示，若直接按照此截面建立轴对称模型，则磁力线主要通过空气路径闭合，而实际的三维结构中，磁力线主要通过磁芯闭合，因此在XP模型中附加了额外的磁芯边柱，使得大部分磁通通过磁芯闭合，以更好地模拟实际变压器的电磁场分布。

图8 XP模型Fig.8 XP model

基于图8（b）所示磁阻模型，XP模型总磁阻RXP可由式（12）求得，其中 Rnear，legs、Rtop，near、Rtop，far、Router分别对应图中所示的磁通流通路径，各磁阻计算所需的尺寸标注如图9所示，同ER模型计算类似，各磁阻值的计算应用式（4）。磁芯中柱磁阻R1保持不变，设磁芯边柱尺寸为m，使得RXP与实际变压器磁阻Rtotal相等，求得磁芯边柱未知尺寸m，磁芯窗口的大小由实际变压器的结构计算，并不要求非常精确，对仿真精度影响不大，磁芯窗口高度e和宽度d的求解如图8（a）和图9（b）所示，得到了这3个未知尺寸，即可建立XP模型。

图9 XP模型磁阻计算尺寸Fig.9 Dimensions of XP model by magnetic resistance calculation

由于实际变压器的磁芯中柱截面为矩形，在建立ER和XP轴对称模型中，需根据等磁阻关系，保持中柱截面积不变，将矩形截面等效为圆形截面，即保持ERXP模型磁芯中柱磁阻R1与实际变压器磁芯中柱磁阻相等，以建立轴对称模型。

2.3 仿真结果及后处理

本文选择了Ansoft公司Maxwell二维电磁场仿真软件，建立ERXP模型来计算变压器的漏感。因为高频涡流效应对变压器磁场分布的影响会表现在漏感上［11-12］，故选择了涡流求解器，仿真不同频率下漏感的变化。变压器漏感表征漏磁通所产生的磁场能量，利用Maxwell后处理求解器得到漏感表征的总能量We，则等效到变压器原边的漏感Lr为：

考虑涡流效应时，ER及XP模型的窗口磁场分布如图10所示。

图10 窗口磁场分布Fig.10 Magnetic field distribution in core window

图中，颜色的变化表征磁场强度的变化，a至q代表的磁场强度分别为：1.2000×104A/m、1.2000×104A/m、1.102 0×104A/m、1.028 6×104A /m、9.5510×103A/m、8.8164×103A/m、8.0817×103A/m、7.347 0×103A/m、6.612 3×103A/m、5.877 6×103A/m、5.142 9×103A/m、4.408 2×103A/m、3.6736×103A/m、2.9389×103A/m、2.2042×103A/m、1.4695×103A/m、7.3480×102A/m、1.1701×10-1A/m。

由仿真结果可见，漏感能量主要集中在初次级绕组之间，与理论分析相符。原边绕组为300 mm×0.2 mm的铜箔，由于端部效应的影响，磁场强度在原边绕组的端部会发生畸变，副边绕组为1.12 mm漆包线，由于涡流效应的影响，电流在导体中并非均匀分布，且绕组高度小于磁芯窗口高度，磁场强度在绕组之间非一维解析算法所假设的线性分布。

ERXP模型中变压器的漏磁通分布如图11所示。由于磁芯相对磁导率为有限值，磁芯中漏磁通的存在会产生一定的漏磁能量，一维解析算法忽略了这部分能量，这在一定程度上也增大了计算误差。二维仿真全面计算了引起漏感的总能量，包括了磁芯、磁芯窗口及磁芯周围仿真区域所有的漏磁能量，提高了计算准确度。

图11 ERXP模型漏磁通分布Fig.11 Leakage flux distribution of ERXP model

由于高频涡流效应对磁场分布的影响，漏感随频率的增大有减小的趋势［8］，利用ERXP模型仿真了频率在10～100 kHz之间变化时，漏感随频率的变化曲线，如图12所示，与理论分析相符，可见在变压器设计时，有必要根据工作频率来计算漏感。

图12 漏感随频率变化曲线Fig.12 Leakage inductance vs.frequency

3 实验验证及结果对比

本文分析的变压器应用在具有容性输出滤波的DCM LCC谐振变换器上，根据输出短路时的谐振电流波形可求得折算到变压器原边的漏感值，如图13所示。图中

图13 初级短路谐振电流波形Fig.13 Waveform of resonant current of primary short circuit

根据式（14）得到折算到变压器原边的漏感值为7.6 μH。图13中谐振电流频率为27 kHz，此时根据ERXP模型仿真的变压器漏感为7.25 μH，变压器漏感理论计算与实验测量结果对比如表1所示。

表1 漏感计算结果对比Tab.1 Comparison of leakage inductance results

由表1可见，以实测结果为基准计算误差，ERXP仿真结果的误差仅为4.6%，比一维解析算法具有更高的准确性。

4 结语

本文以高压大功率LCC谐振变换器为应用背景，利用二维有限元仿真软件，分析了一个原副边绕组同心柱绕制，磁芯中柱为矩形截面的E型变压器漏感计算问题。比较了几种不同的计算方法，结合实际变压器的结构和工作特点，对ERXP二维轴对称模型进行改造后加以应用，得到了与实测结果相比误差较小的漏感仿真值，证明了建模的正确性，在此基础上，进一步探讨了高频涡流效应对漏感的影响。在绕制变压器之前，利用ERXP二维模型仿真变压器的漏感值，将为变压器的设计、谐振变换器整体电路设计和控制方式的选择提供很好的指导。