龙门式数控铣床床身动态特性分析
2013-10-17梁双翼尹辉俊罗海萍
梁双翼,陈 晨,尹辉俊,罗海萍
LIANG Shuang-yi,CHEN Chen,YIN Hui-jun,LUO Hai-ping
(广西科技大学 机械工程学院,柳州 545006)
0 引言
数控机床是一个多自由度振动系统,在加工过程中会有各种激振力作用于机床上,这些激振力是数控机床产生复杂振动的振源。当这些激振力的激振频率恰好和整个数控机床的某一阶固有频率相吻合时,就会发生共振,导致在数控机床上某些部位产生数值很大的共振动应力,从而影响数控机床加工精度和工件的表面光洁度。因此,对数控机床床身动态特性进行研究分析具有十分重要的意义。对床身进行动态特性的分析主要是研究床身抵抗振动的能力,本文以某型龙门式数控铣床为例,采用有限元分析方法对其床身进行动态特性分析,为数控机床床身的优化设计提供依据。
1 激振力分析
数控机床在加工过程中所受的激振力是机床产生复杂振动的振源。产生这些激振力的原因主要有三类:第一,机床各相对运动部件摩擦表面上有摩擦力的作用;第二,机床回转部件不平衡等因素使回转系统受到离心力的作用;第三,刀具切削工件使整个机床系统受到切削力的作用,这些切削力并非保持常值,有的是周期性变化的,有的可能和机床系统某些元件的位移、速度或加速度等参数有一定关系,有的则和系统某些元件的刚度轴线有一定的方向关系等。
2 多自由度振动系统的计算机解法
对数控机床动态特性的研究内容包括固有特性和动力响应的研究,确定数控机床的动态特性参数。研究方法是建立机床的动力学微分方程,通过求解运动方程组的特征值和特征向量,得到机床的固有频率和振型,在此基础上进行动力响应分析。
无阻尼系统受迫振动微分方程为:
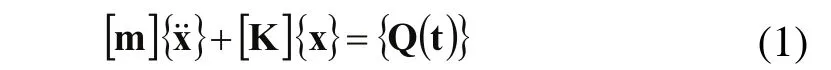
其中,[M]为总质量矩阵,[K]为刚度矩阵,{X}为节点位移列矩阵,{Q(t)}为激振力列矩阵。
在铣刀的每一个刀齿铣削工件时,就会有周期性的激振力作用在主轴上,相当于主轴上有简谐激振力的作用,则:
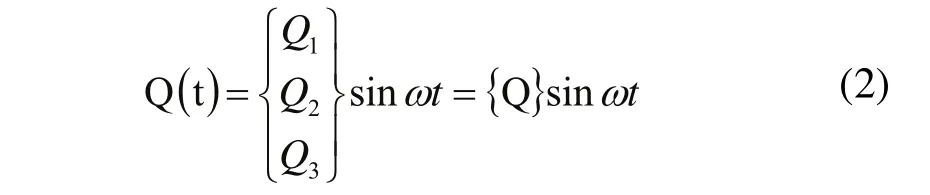
则系统受简谐激振力时的运动微分方程为:

采用坐标变换法,将运动微分方程采用{x}=[N]{ø}进行变换,即:
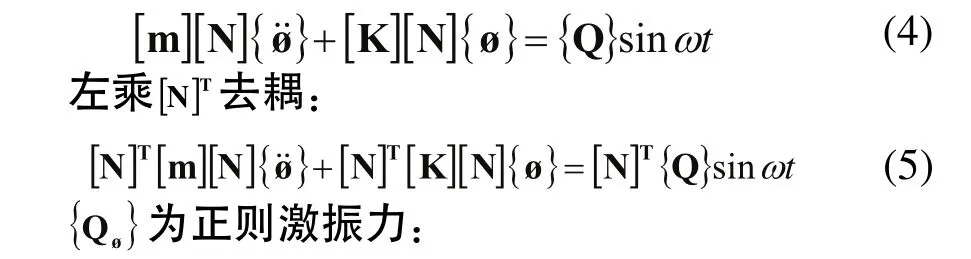

将系统正则方程展开,得到n个单自由度系统强迫振动的形式:
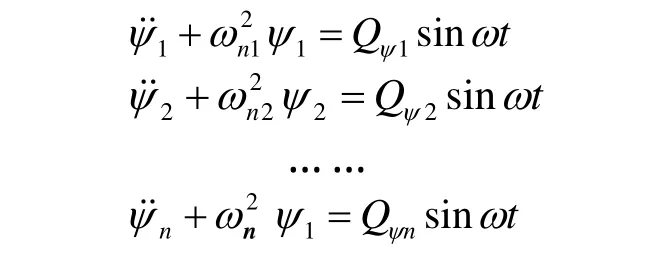
以上各方程可单独求解:
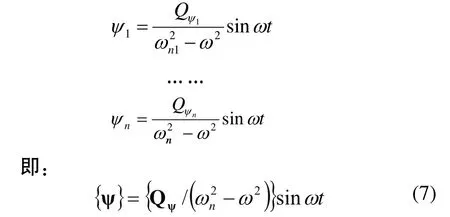
用{x}=[N]{ψ}进行坐标反变换,即可得到系统的稳态响应:

当激振力频率接近固有频率ωn1,ωn2,…中任何一个值时,系统振幅将有最大值,发生共振,n个自由度有n个共振频率。
当系统自由度较少时,可以通过求解系统的特征方程,求出特征根,即固有频率的平方值,由此可解出固有频率ωn,然后再求出系统的特征向量,即主振型。但对于多自由度系统,求解固有频率的计算量将惊人地增加,需要借助计算机来求解[1]。在有限元分析软件MSC.Nastran中提供了7种实特征值提取方法,其中推荐使用Lanczos法。因Lanczos法不会丢根,且它仅计算用户要求的根,因而求解效率高,非常适合解算大部分中、大型问题[2]。
3 有限元计算
3.1 龙门式数控铣床床身有限元模型的建立
考虑到龙门式数控铣床床身的几何复杂性,先在三维CAD软件中建立床身的三维模型,对局部结构作适当简化后,以STEP.x_t格式导入MSC.Patran中,如图1所示。
采用四节点四面体单元Tet4对床身划分网格,取单元边长为100mm。定义单元材料属性,取杨氏模量E为2×105Mpa,泊松比为0.3,密度为7.8×103kg/m3。在施加边界约束条件时,考虑到床身底座与地基固连,将床身底座全部约束,在主轴前端施加2228N的切削力,划分网格并施加约束后的模型如图2所示。
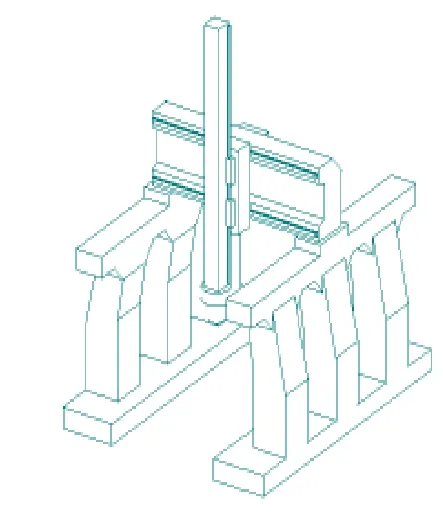
图1 床身三维模型
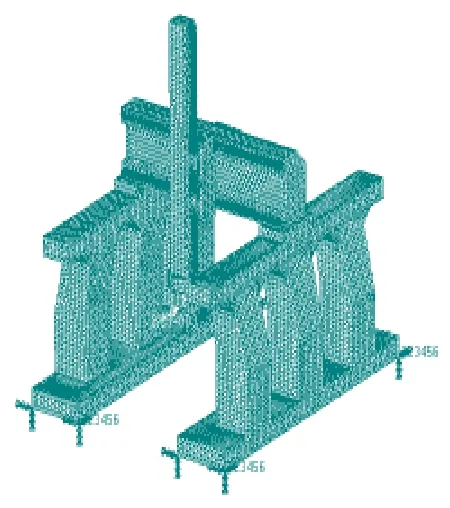
图2 床身有限元模型
3.2 计算结果分析
将模型提交MSC.Nastran进行模态分析,提取前5阶模态分析结果,固有频率和振型描述见表1所示,振型如图3~图7所示。
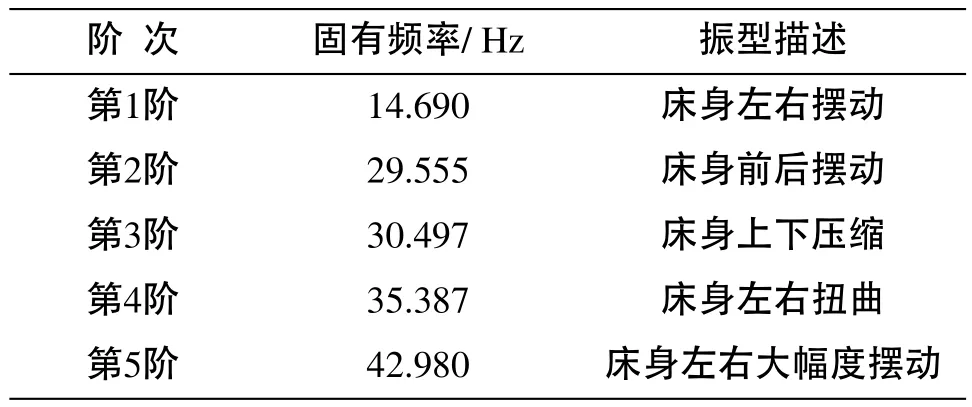
表1 机床床身前5阶固有频率和振型结果

图3 床身第1阶约束模态振型

图4 床身第2阶约束模态振型

图6 床身第4阶约束模态振型

图7 床身第5阶约束模态振型
由模态分析结果可知,机床的振动、变形主要在主轴前端、横梁和立柱处,其中以主轴的振动、变形最明显。但变形量均不大,对加工精度影响不大。机床第一阶固有频率略低。由于该型龙门式数控铣床的实际工作转速范围为20~7000r/min ,因此机床在加工过程中最有可能出现接近表1中的低阶固有频率,会引起机床共振,对这些频率下机床的振动情况加以研究就显得格外重要。
4 床身测试试验分析
为了初步验证用有限元分析软件来分析机床固有特性和动态特性的有效性,对该型龙门式数控铣床做了测试试验,分为空运转试验和切削试验。
4.1 机床空转试验
空转试验是在机床按加工状态运转但并不进行切削的过程中,测量机床部件的指定点的振动情况。通过空转实验可以暴露出机床可能存在的缺陷,发现引起受迫振动的根源。
4.1.1 试验方案
在不切削、不进给条件下启动主电机,将电主轴转速由低到高加速到5000 r/min~7000 r/min左右的转速进行空运转,测出在此运转条件下电主轴前支承位置测试点处的振动加速度响应。
4.1.2 试验装置
测试系统采用北京东方振动与噪声控制工程研究所研制的INV306U型智能信号采集处理分析仪、9818型压电加速度传感器和DASP软件系统。
4.1.3 试验结果和分析
起动机床主电机后,先让主轴运转一段时间,分别在主轴转速到达5000r/min和7000r/min时采样,由DASP软件分析测量数据,输出自谱分析结果,如图8和图9所示。
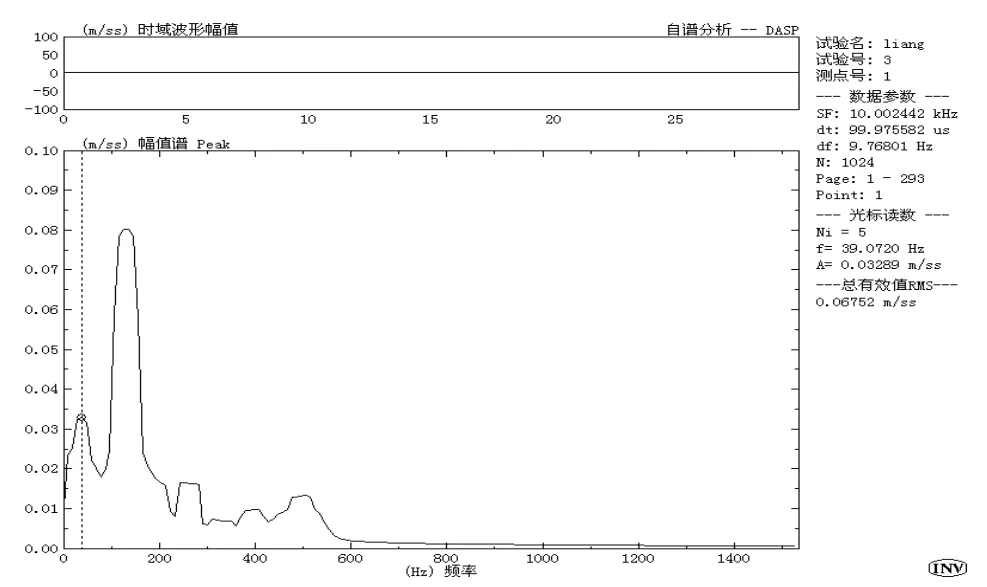
图8 5000r/min测试结果
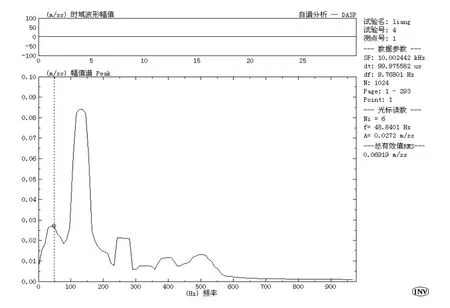
图9 7000r/min测试结果
由上述实验测试结果可知:该机床可能存在频率为39.07Hz和48.84Hz的两个振源,幅值分别为0.03289m/s2和0.0272m/s2。除了回转部件的不平衡导致的强迫振动外,其中一个可能的震源是机床电机,有待进一步验证。
4.2 机床空转试验
4.2.1 试验方案
采用高速钢镶片铣刀铣削试件,切削深度为5mm,分别做了4组试验。切削试件材料为钼铬合金铸铁,试验装置与空转试验相同。
4.2.2 试验结果和分析
由DASP软件分析测量数据,输出自谱分析结果,得到4组试验结果如表2所示。限于篇幅论文只列出了第1组频谱图,如图10所示。

表2 切削试验结果
由表2的切削试验结果可知,该机床存在的低阶频率为29.3040~30.9630Hz左右的薄弱模态。对比空转试验和切削试验的频谱图,可知机床切削状态与空转状态的低阶频率相近,只是波形图有少许变化。初步分析认为与空转试验的情况类似,是由于回转部件不平衡引起的机床固有振动。
4.3 试验结果与有限元分析结果比较
对比有限元分析结果可知,试验结果与有限元分析结果非常接近,其误差均在允许的范围内。对于没有测试出第一阶的频率14.690 Hz,是因为试验条件有限,无法激振出此阶频率。由试验结果可作出结论:本文所用的有限元建模和分析方法对于该型龙门式数控铣床床身的分析研究是合理有效的。
5 结束语
本文对某型龙门式数控铣床床身的动态特性进行了有限元分析,并通过试验验证了有限元分析方法的合理性,获得床身的动态特性参数,为床身的结构改进设计提供了理论依据,并为进一步建立机床系统的振动方程,预估机床在外力作用下的响应,为深入研究机床的振动、疲劳和噪声等问题奠定了基础。
[1] 邵忍平.机械系统动力学[M].北京:机械工业出版社,2005:128-128.
[2] 隋允康,杜家政,彭细荣.MSC. Nastran有限元动力分析与优化设计实用教程[M].北京:科学出版社,2004:43-43.
