深孔钻削中工件的动力学特性研究
2013-10-17马广轩庞俊忠郑志群
马广轩,庞俊忠,郑志群
MA Guang-xuan,PANG Jun-zhong,ZHENG Zhi-qun
(中北大学 机械工程与自动化学院,太原 030051)
0 引言
深孔钻削中的振动往往是影响工件加工质量、限制加工效率的主要因素之一。如果振动严重,还会使刀具过度磨损甚至导致崩刃。因此,对深孔钻削过程中颤振的研究一直是深孔加工领域的热门课题之一。
国内学者从深孔钻削失稳的主要原因、深孔加工瞬时动态切削力与颤振机理、稳定加工的临界条件[1,2]、深孔钻削动力系统的弯曲变形等几个方面进行了研究[3]。国外学者则通过对深孔钻削颤振测量实验的结果进行时域及频域分析,从而得到不同钻削深度下颤振的本征频率及振幅[4]。德国学者利用Dexel模型对深孔加工圆度误差进行了仿真,在与实验结果进行对比分析后指出仿真结果的误差的产生应该是由于未考虑加工过程中刀具磨损及工件状态的改变[5]。
针对等截面梁振动的研究现已比较完善,而对变截面梁振动进行的研究多集中于对自由振动特性的分析[6,7]。而金属切削加工过程中工件的振动情况属于受迫振动。本文结合深孔加工的实际情况,把深孔钻削加工中的工件简化为两端固定支承的、轴向移动载荷作用下的变质量和变刚度的阶梯梁。通过分析阶梯梁的受迫振动,得到了以工件固定、刀具旋转进给为加工方式的大长径比薄壁孔工件的动态响应特性。同时为研究深孔加工过程中工件的振动问题提供了新的思路及方法。
1 深孔钻削工件振动模型
BTA深孔钻削过程如图1所示。具有一定压力的切削液通过钻杆外部的环状空隙流向切削刃部,将切削刃上形成的切屑反向压入钻头的出屑口,经钻杆的中空内腔向后排出。加工有两个运动部分组成:刀具和工件,工件一端被固定在卡盘上,另一端顶悬在导向套上。工件固定,刀具旋转并沿工件轴向做直线移动。
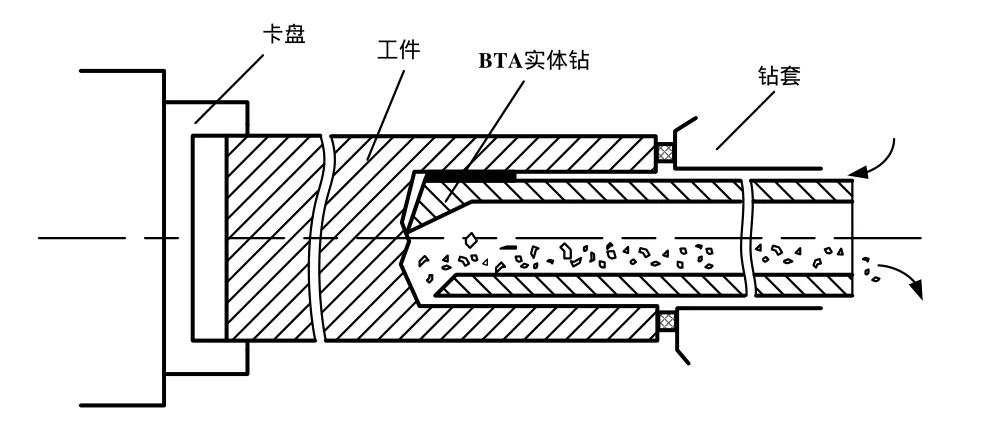
图1 BTA深孔钻削示意图
由于工件两端分别固定在卡盘与导向套上,工件两端的横向位移与转角均为零,所以可将工件简化为两端固定支承的变截面梁。以工件在导向套固定端的轴心为直角坐标系xOy的原点O,x轴及y轴正方向如图2所示,建立深孔钻削工件的动力学模型。
工件在加工过程中可分为三部分:待加工部分、已加工部分及在加工部分。由于在加工部分在大长径比工件中所占比例相对较小,可作如下假设:1)将在加工部分的长度并入已加工部分;2)将在加工部分假设为刚体。假设1)将工件变为两部分:第一部分B1为在加工部分及已加工部分的总和,其长度为l1,截面惯性矩为I1,截面积为A1,孔径为d;第二部分B2为待加工部分,其长度为l2,截面惯性矩为I2,截面积为A2,直径为D。工件全长为L,弹性模量为E,密度为ρ。由假设 2)及刚体力的可传递性原理,可将纵向切削力Fy沿其作用线平移至在加工部分的外表面,切削力的横坐标为 l1=l −l2=vft ,其中vf为钻削进给量,n为转速。

图2 深孔钻削工件模型
2 动力学方程的建立及分析计算
2.1 动力学方程
设y(x,t)为梁的横向位移量,则图1所示的深孔钻削工件动力学模型对应的变截面Eular—Bernoulli梁模型的动力学方程为:
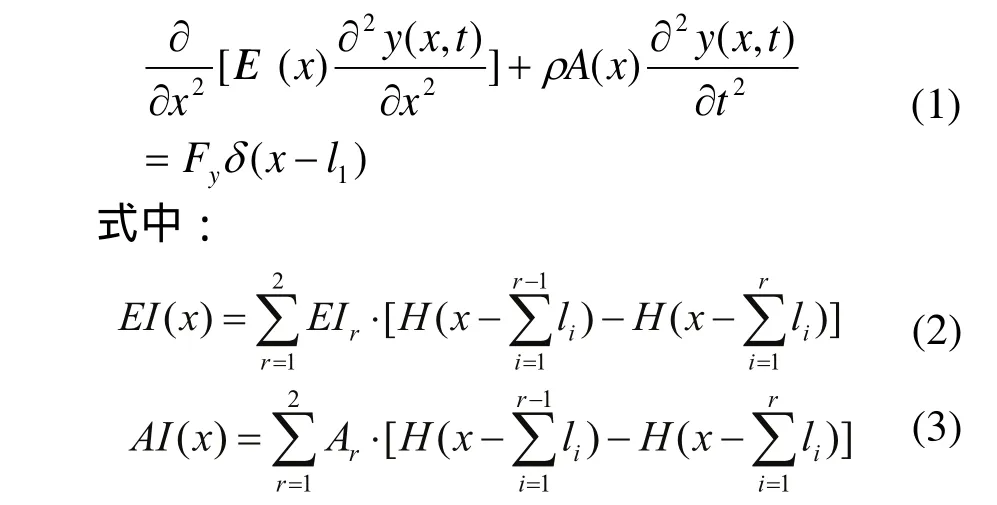
H (x)为Heaviside函数,l0=0,0<x<l时,H(x−l0)=1,H(x −l)=0;δ(x)为Dirac函数。
2.2 自由振动方程的分析计算
当Fyδ(x−l1)=0时,可得到变截面梁的自由振动方程。设 y(x,t)=Y(x)Φ(x),将 y(x,t)对t和x分别求二次和四次偏导得:

将上两式带入自由振动方程并分离变量可得:
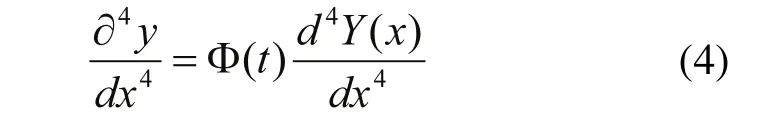


式中yij(x)为第i段梁的模态函数。
由(6)式可得第i段轴两端状态矢量的传递关系为:

工件两端分别用卡盘及导向套固定,由两端固支梁的边界条件可知:
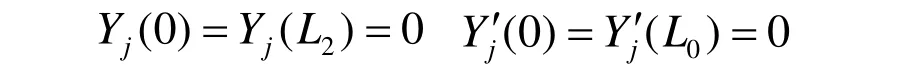
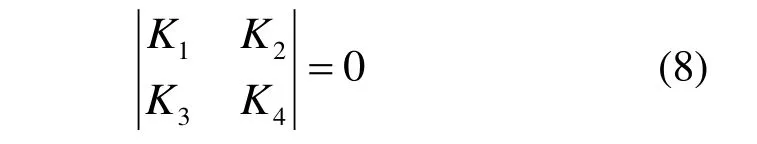
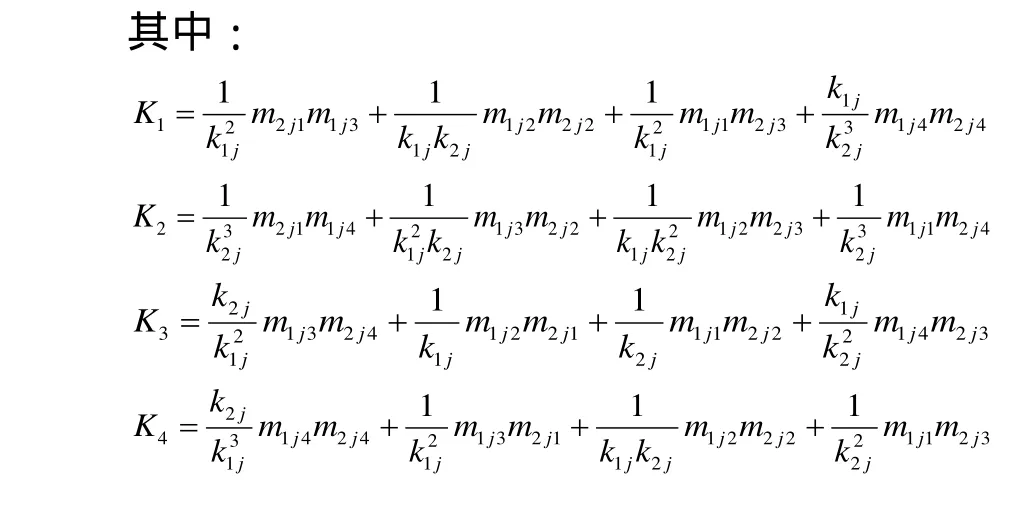
2.3 受迫振动方程的分析计算
等式(1)的解可用模态分析法求得。假设梁的垂直位移为:
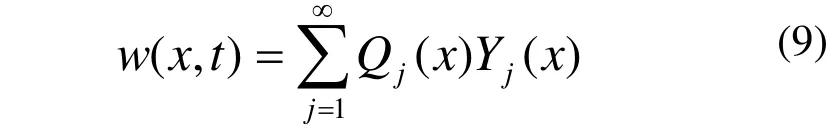
其中Qj(x)为总体未知时间函数,将式(9)代入式(1),等号两边同乘以Yk(x)并对梁的全长积分,则有:
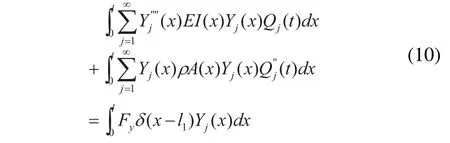
梁的广义刚度与广义质量为:

由主振型的正交性性质可知kjk=mjk=0(i≠j)。

则梁的第j阶固有频率:

利用Dirac函数的性质可得到模型的广义激振力为:

将式(11)、(12)、(13)、(14)代入式(10)可得到系统的第j阶模态方程为:

其中ti为载荷走过第i段梁所需的时间。
3 数值计算及分析
以钻削45号钢为例进行数值计算,工件长度为1000mm,工件外径为40mm,内孔直径为20mm,弹性模量 E=210G Pa ,密度ρ=7.85g/cm3。以工件固定,刀具旋转并进给的方式进行加工,转速为800r/min,进给量为0.12mm/r。由文献[8]计算可得此时的径向切削力约为1500N,将以上数值代入式(1)进行计算,得到钻削至250mm和500mm时工件模型的前五阶固有频率如表1所示。

表1 钻削至不同位置时工件固有频率
由表1可知随着加工的进行工件的固有频率逐渐增大,这是由于随着加工的进行工件的质量及刚度发生改变造成的。再分别计算出不同加工位置时的主振型及未知时间函数。文献[9]提出对前五阶振型进行计算即可满足一般精度要求,对前五阶振型进行叠加得到不同加工位置时工件的振动情况如图3、图4所示。
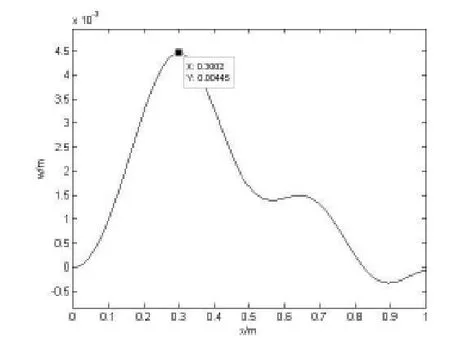
图3 钻削至250mm时工件振动情况

图4 钻削至500mm时工件振动情况
图3为加工至250mm时的动态响应,图4为加工至500mm时工件的动态响应。对比图3及图4可知:径向切削力将导致大长径比工件在钻削过程中出现较大振幅,为保证加工质量需在工件上加装起辅助支撑作用的中心架;最大变形出现在径向切削力所在位置的附近,所以在加工过程中应随着加工进程适当改变中心架位置;相对于加工至250mm时的变形,加工至工件中心处的变形最大,此时可适当增加工件中心架数量以提高工件的刚度。
4 结论
本文研究了变截面梁在移动载荷下的动态响应,并以此为基础建立了深孔加工过程中工件的振动模型及动力学方程,其中考虑了加工过程中工件质量和刚度变化对工件振动的影响。通过对动力学方程进行计算,得到了工件模型的动态响应,为研究深孔加工过程中工件的振动问题提供了新的思路及方法。 再以加工45号钢工件为实例对工件模型进行数值计算,得到以下主要结论:
1)工件振动的固有频率并非一成不变,而是在加工过程中随着加工的进行逐渐增大;
2)不同加工位置的振型并不相同,最大变形一般出现在切削力所在的位置附近;
3)加工至中点时振幅明显大于加工至其他位置时。在加工过程中应适时改变工件中心架的安装位置及安装数量以降低振动幅度,提高加工质量。
[1] 袁忠于.深孔钻削加工的振动分析及仿真[D].兰州理工大学,2005.
[2] 李琦,裴宏伟,于勇波,郭成.BTA深孔钻切削实验研究[J].机械设计与制造,2004(1):105-106.
[3] 玛嘎拉.高速微孔钻床主轴系统及钻头的动态特性研究[D].吉林大学,2005.
[4] K.Weinert,0.Webber,C.Peters. On the In fluence of Drilling Depth Dependent Modal Damping On Chatter Vibration in BTA Deep Hole Drilling[J].CIRP Annals - Manufacturing Technology,2005,54(1):363-366.
[5] Dirk Biermann.etc. Simulation of the BTA deephole drilling process[J].Production Engineering,2009,3(4-5):339-348.
[6] 崔灿,蒋晗,李映辉.变截面梁横向振动特性半解析法[J].振动与冲击,2012,31(14):85-88.
[7] 黄志杰.阶梯梁弯曲自由振动的特征方程[J].长沙水电师院自然科学学报,1994,9(1):94-99.
[8] 王峻.现代深孔加工技术[M].哈尔滨:哈尔滨工业大学出版社,2005.
[9] 肖新标,沈火明.移动载荷作用下桥梁的系统仿真[J].振动与冲击,2005,24(1):121-123.
