基于双因素加速寿命法的导弹火工品可靠性评估＊

张晓民 刘洪浩 李晓宁

（91049部队 青岛 266102）

1 引言

文献［1］定义火工品的可靠度是火工品在规定条件下和规定时间内，完成规定功能的能力。

从定义可知可靠性是与“规定的条件”分不开的，这里所说规定的条件是指使用时的环境条件（温度、湿度、振动、冲击、辐射）、使用时的应力条件、维护方法、贮存时的贮存条件和使用时对操作人员技术等级的要求等。因此在不同的规定条件下产品的可靠性是不一样的。

贮存可靠性是一项复杂的系统工程。研究贮存可靠性不仅有重大的经济意义，更具有重要的军事意义。贮存期短，就会不必要地提前更换有关的元器件和零部件，造成巨大的人力、物力和经济浪费。如果盲目地把贮存期定长了，轻则会影响产品使用效果，重则可能造成重大事故。

2 传统火工品可靠性评估方法

2.1 二项分布估计可靠度

文献［2］中规定，统计可靠性试验中试验数n、失效数F，当批量N满足N≥10n时，在置信水平γ，可靠度R由式（1）或式（2）求出。

由这两个公式可知，假设参与验证可靠度的一批样品没有一个发生失效，那么要达到产品在置信度γ为0.90、可靠度R为0.9999的要求，则需要样品数量为23026发。

2.2 超几何分布估计可靠度

文献［2］中规定，统计可靠性试验中试验数n、失效数F，当批量N满足N≤10n时，在置信水平γ，可靠度R由式（3）求出。

在置信度γ为0.90的情况下，当批量N为1500发，试验数n为800发，失效数F为0，通过式（3）计算出可靠度R也仅为0.9980。

通过上面分析可知，如果单纯通过计数法要达到产品需要的高可靠度需要大量的样品做实验才能得出高可靠性的结论。

上述常规的寿命评估方法归属于概率和统计论的范畴，因而所需的子样数较多。由于导弹价值昂贵，每枚导弹上的火工品数量有限，通过对上述传统可靠性方法分析可知，要完成对长贮火工品的可靠性评定需要大量的长贮火工品样本进行试验验证，因此用传统的可靠性评定方法显然不可行。如何在小子样的条件下完成对长贮导弹火工品的寿命评估，针对这个问题，本文提出双因素加速寿命试验法，对火工品进行相应时间的加速寿命试验，将加速不同年限的火工品进行发火电流的测试试验，通过试验数据建立可靠度R与时间t的函数关系式，从而对导弹火工品的剩余寿命进行评估。

3 双因素加速寿命试验法

双因素加速寿命试验法指的是利用温度和湿度两个因素对火工品样本进行加速寿命试验，得到所需要的试验样本，然后将加速不同年限的火工品进行发火电流的测试试验，通过试验数据建立可靠度R与时间t的函数关系式，从而对导弹火工品的剩余寿命进行评估。

3.1 试验样本数量的获取

因为用于试验的导弹数量有限，其火工品数量并不能满足试验所需的样本量，因此利用仿研制造得到所需要的样本数量。

仿研制造研究工作程序分为四个阶段。

1）解剖测绘

（1）样品、部件、分部件解剖测绘：首先将样品进行X光照相以及CT照相，理清解剖路线，画出部件图，逐步绘出部件、分部件图，并收集解剖分离出的所有物质（金属、非金属材料）待理化分析，照相后分别编号包装储存备案。

（2）零件解剖测绘：解剖后的每个零件首先照相（或录像），测绘尺寸画出图形、理化分析材料（含各种用胶、油脂等所有材料）成分、理清原始状态。

2）反设计

按照理清的原始状态测绘图形尺寸、材料成分，设计制造公差。

3）加工制造

按照反设计图纸安排加工，机加件机械制作，需要模具加工的配做成形模具（含非金属件），与国家标准同等的零件直接订购。

4）验证试验

对国产化的零件，按反设计图纸要求验收合格进行装配部件、分部件验证适配性和功能试验，鉴定国产化仿研件的可靠性。

通过上述四个步骤可以获得所需的试验样本数量。

3.2 不同年限试验样本的获取

双因素加速寿命试验的基本思想是利用高应力下的寿命特征去外推正常应力水平下的寿命特征。其关键在于建立寿命特征与应力水平之间的关系，由此就可以实现外推正常应力水平下寿命特征的目的。这种寿命特征与应力水平之间的关系就是加速模型，又称加速方程［3］。

加速模型一般可分为物理加速模型和数学加速模型。物理加速模型从物理学的角度去定义加速模型，侧重于定性分析；数学加速模型从数学公式的角度去定义加速模型，侧重于定量分析［4］。

目前物理加速模型较多，常用的共五种。包括阿伦尼斯模型（Arrhenius Relationship）、艾林模型（Eyring Relationship）、逆幂律模型（Inverse Power Law Relationship）、温度—湿度模型 Temperature－Humidity Relationship）、温度—非热模型（Temperature－Non Thermal Relationship）。每种模型的应用场合和特点各有不同，阿伦尼斯（Arrhenius）寿命—应力模型是加速寿命试验中应用最为广泛的一种模型。它是指以热能（如温度）作为加速应力的加速模型［5］。逆幂律（Inverse Power Law）模型一般用在以电压为加速应力的场合［6］。艾林（Eyring）模型来源于机械原理，广泛应用于热应力加速试验中［7］，其模型方程式有时也用于非热应力，如湿度等的加速寿命试验场合。温度—湿度（Temperature－Humidity）模型是双应力加速寿命试验模型［8］，它应用于使用温度和湿度同时作为加速应力的场合，此模型是从艾林模型变化来的。温度—非热（Temperature－Non Thermal）模型也是一种双应力加速模型，它应用在以温度和另一个非热的应力为加速应力的场合［9］。

火工品的贮存寿命主要受温、湿度的影响，因此常温、常湿下的贮存寿命一般是要通过温、湿度双应力加速寿命试验，求得加速方程，外推得出。

1）方法原理

双因素模型和加速系数定义为［10］

式中T0为常温绝对温度，K；T1为试验绝对温度，K；RH0为常湿相对湿度；RH1为试验相对湿度；B、C、D为分别温湿度加速寿命方程中的温度项、湿度项、温湿度交互项的系数；R为理想气体常数；τ为温湿度总加速系数。

如果用τ1、τ2、τ3分别表示方程中的温度、湿度、温湿度交互项加速系数。式（4）则可写成：

由加速寿命试验贮存时间t1，要推得试样在常温常湿下贮存寿命t，则有：

规定的试验条件范围（温度50℃～70℃、相对湿度80%～95%）

2）贮存寿命评估

根据性能测试结果，依据火工品的技术条件，判断试样是否全部合格。若进行的试验项目技术条件无规定，应按照文献［11］中规定的t检验法，作出是否发生显著性变化的结论。若经本方法试验，测试结果全合格（或经检验无显著性变化）按照式（6）作出贮存寿命评估。式（6）中各项参数按以下公式计算和取值：

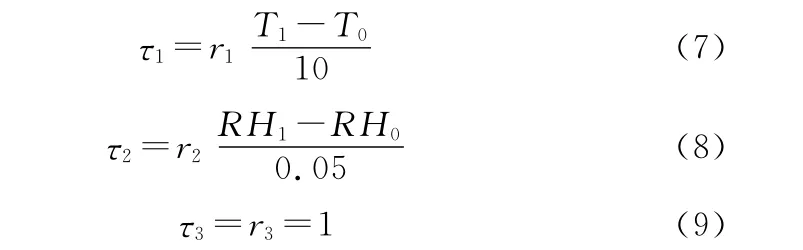
式中r1为温度每升高10℃反应速度加快的倍数，取2.7～2.9；r2为湿度每升高5%反应速度加快的倍数，取2.0；r3为等于r2，取值为1.0。

其中，试验条件为温度70℃、相对湿度为95%情况下r1取2.7，试验条件为温度50℃、相对湿度为95%情况下r1取2.9。计算结果在15年以下取整数，在15年以上只按15年计算。

根据双因素加速模型，在温度为50℃、相对湿度为95%的试验条件下，根据式（7）～（9）可得：

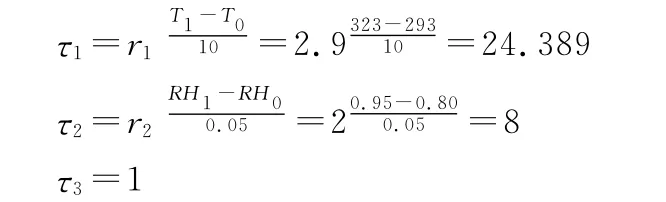
因此，例如要得到等同于15年长贮样本，根据式（6）计算所需要的试验时间t1为

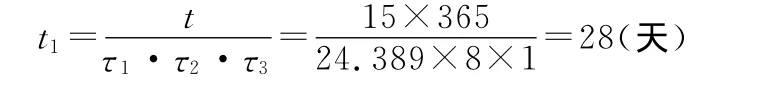
因此，通过式（6）可以计算出相当于长贮时间为ti的试验样本需要进行加速寿命的时间。

4 数值算例

某导弹上火工品样本可靠性指标γ＝0.9，R＝0.9999。发火要求是起动电流不小于1.5A，即规定的最小全发火电流为1.5A。电爆管主要技术指标如表1所示。

表1 电爆管主要技术数据

由于产品没有升降法试验数据或其它感度试验数据，也没有贮存时间为ti（i＝1，2，…，k）的产品。这里，按照要求，在产品没有升降法试验数据和其它感度试验数据时，需要先进行一组样本量为30的升降法预试验，根据试验结果并结合工程经验确定初始刺激量X0和步长d，再加上用于升降法的5组各30发样品，一共需要仿研火工品数量为180发。再按照要求对样品进行加速寿命试验，按照式（6），分别得到等同于贮存时间为2，4，6，8，10的加速样品各30发。将这些样品分别进行升降法试验，设得到数据（i＝1，2，…，k）并对试验数据进行处理。由此可得其贮存可靠性模型。因为目前无条件进行该试验，这里应用参考文献［4］的数据进行说明。

某撞击火帽贮存可靠性指标为γ＝0.9，R＝0.999，落锤重量（388±1）g，落高100mm。现要评估产品贮存15年的可靠性，并预测满足可靠性指标的贮存寿命。该火工品服从正态分布，其在贮存时间t时刻的产品的临界刺激量x（t）服从分布参数为μ（t）与δ（t）的正态分布可靠性估计模型为

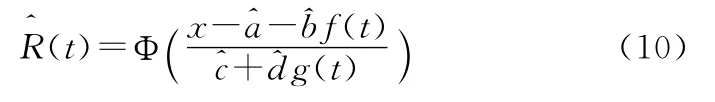
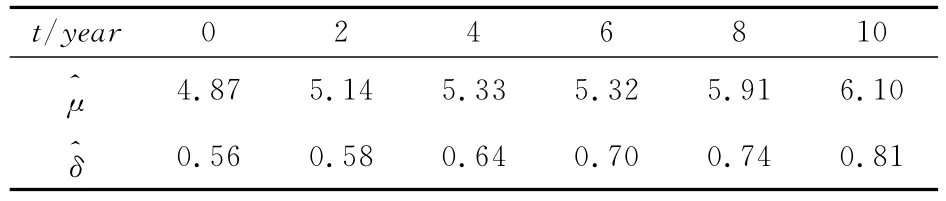
表2 火工品感度分布参数估计

对表2的数据进行处理使其满足序约束条件，然后对其进行统计分析，利用式（10）可得产品在贮存时间t时的可靠度估计：

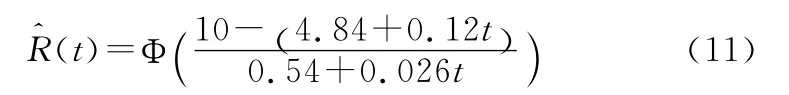
经查表可得贮存时间为15年时产品可靠度近似下限为0.9998，故该火工品在贮存时间为15年时满足可靠性指标要求。同时根据产品的可靠度下限，利用式（11）可得该产品满足指标要求时的贮存寿命近似下限t为16.9年，与实际情况相符。

5 结语

通过分析传统火工品贮存可靠性的评估方法存在的不足，将双因素加速寿命法应用于某导弹火工品的贮存可靠性评估。具体介绍了试验样本数量的确定方法，不同年限试验样本的获取方法，通过实例分析了双因素加速寿命法的具体应用，计算结果与实际情况相符，说明该方法适用于导弹火工品的贮存可靠性评估。

［1］国防科学技术工业委员会.GJB102A－1998，弹药系统术语［S］.西安：中国兵器工业集团第二一三研究所，2010（05）.

［2］国防科学技术工业委员会.GJB376－87，火工品可靠性评估方法［S］.西安：中国兵器工业集团第二一三研究所，2010（05）.

［3］林震，姜同敏，程永生，等.阿伦尼斯模型研究［J］.可靠性与环境适应性理论研究，2005，12（6）：12－14.

［4］唐天元.加速寿命试验数据管理与解析系统研究［D］.哈尔滨：哈尔滨理工大学，2007.

［5］L.A.Escobar，W.Q.Meeker.Planning accelerated life tests with two or more experimental factors［J］.Technometrics，1995，37（4）：411－427.

［6］苑中魁，王少萍.一类解决变应力加速寿命试验参数估计的方法［J］.北京航空航天大学学报，2005，31（11）：1172－1175.

［7］Zhang J.P.，Geng X.M..Constant－step stress accelerated life test of VFD under weibull distribution［J］.Journal of Zhejiang University，2005：6（7）：722－727.

［8］张春华，陈循，李岳.一种新的分布恒定应力加速寿命试验分析方法［J］.国防科技大学学报，2002（24）：81－84.

［9］韩明.位置－尺度参数模型的可靠性分析［J］.兵工学报，2006，26（4）：690－694.

［10］中国兵器工业集团第二一三研究所.Q／AH0180－93，火工品加速寿命试验——高温高湿试验法［S］.西安：中国兵器工业集团第二一三研究所，1994（01）

［11］国防科学技术工业委员会.GJB736.8－90，火工品试验方法71℃实验法［S］.西安：中国兵器工业集团第二一三研究所，2010（05）.