基于AHP和模糊综合评判法的登陆作战效能分析＊

2013-10-16陈松辉邱宏理

舰船电子工程 2013年2期

陈松辉邱宏理

（海军陆战学院广州 510430）

1 引言

现代登陆作战中，由于武器装备科技含量的不断提高，使得登陆战斗对抗强度日益激烈，其作战效能的高低直接影响着战斗的胜负；而决定作战效能的因素较多，不同的作战任务各因素的影响限度也不同。我们运用层次分析法来确定影响登陆部队作战效能的各指标的权重，使用模糊决策方法对模糊指标进行评价，从而为科学合理地确定登陆部队兵力编成提供了一种论证方法和参考依据。

2 流程分析

运用AHP与模糊综合评判法的分析，是对AHP法的补充和验证，主要分析流程如下：

2.1 AHP法确定目标编成权重

AHP法主要特点是把复杂的问题分解为若干层次组成因素，将这些因素进行两两比较，确定同一层次中诸因素的相对重要性，然后综合各层次的结果以研究确定各因素相对于总体目标的重要性［1］。

2.1.1 构建指标体系及其层次结构

建立层次模型时，同一层次的元素作为准则对下一层次的某些元素起支配作用，同时它又受上一层次元素的支配，这些层次大体可以分为三类：第1层是目标层，中间层可包含多个层次，最末层由方案、指标等构成［2］。

2.1.2 构造两两判断矩阵

在建立递阶层次结构以后，上下层之间元素的隶属关系就被确定了。假定以上一层元素A为准则，所支配的下一层元素为Bi（i＝1，2，…，n）。针对A 而言，领域专家对Bi（i＝1，2，…，n）和Bj（j＝1，2，…，n）进行两两比较判断［3］，判断结果可用萨蒂对于因素两两比较时相对偏好判断的九级标度（见表1）：

表1 因素两两比较时相对偏好判断的九级标度

通过因素的两两比较建立判断矩阵

2.1.3 计算各元素相对权重向量

各元素相对重要性权重向量

可得出W＝（w1，w2，…，wn）T即为权重向量。

2.1.4 一致性检验

由以上结果，计算矩阵B的最大特征根

表2 不同阶数的平均随机一致性指标RI

当CR＜0.1时，认为判断矩阵的一致性是可以接受的。当CR＞0.1时，应该对判断矩阵作适当修正。

同理，可逐层构建判断矩阵，得到最底措施层相对权重C＝｛c1，c2，…，cn｝。

2.2 模糊综合评判

模糊综合评判是考虑事物的多种因素，用模糊数学理论判定其优劣的一种方法［4］。

2.2.1 确定模糊综合评判要素

由上述结果可得模糊综合评判的三个要素：

1）系统A的各因素相对权重集C＝ c1，c2，…，c｝｛

n，即被评判对象的各因素组成的集合；

2）判断集V＝ v1，v2，…，v ｝｛

n，评语组成的集合；

3）单因素判断，即对单个因素ci（i＝1，2，…，n）的评判，得到V 模糊集（ri1，ri2，…，rim），所以它是从C到V 的一个模糊映射：

2.2.2 确定评判矩阵

模糊映射F可以确定一个模糊关系R∈Un×m，称为评判矩阵

它是由所有对单因素评判的模糊集组成的。

2.2.3 计算评判函数

1）一级综合评判

一级综合评判模型C◦R＝D＝（d1，d2，…，dm）

dj是r1j，r2j，…rnj的函数，是评判函数。

2）多级综合评判

通过一级综合评判模型公式可以看出，各因素的权重对计算结果有直接的影响。当要评价对象的因素很多时，各权重值通常很小，在取“最小”的运算中，就会被取上，这就失去了权重的意义。另一方面，因素很多时，权重也难以确定下来，即使确定下来，也难以反映各因素在整体中的地位。此时，要用多级模型。多级模型的综合评判，是将评价对象的要素集C分为p个互不相交子集Ci（i＝1，2，…，p），对每个子要素集Ci确定权重并进行评价，得到每个子要素集的评价矩阵，然后按照一级评判模型公式可得到综合评判［6］。本文在此不做重点讨论。

3 实例应用

3.1 构建登陆作战效能评估体系

登陆作战效能评估指标体系的影响因素较多，在实际评估中，我们既要全面考虑各种影响因素，又要对各因素进行适当的取舍，对一些没有直接影响的指标可忽略，对有相似影响的因素进行合并归整［7］。为简化流程，现从以下四个主要方面着手建立：火力打击能力、机动能力、防护能力和保障能力。在以上分析的基础上，建立如下的指标体系（如图1）［8］。

图1 登陆作战效能评估指标体系

3.2 使用AHP法确定各指标权重

3.2.1 构造判断矩阵

如图1所示，相对于各个上层元素，我们采用1～9标度的专家赋值法对同一下层中的各元素进行两两比较、判断确定下层元素对上层某一元素的相对重要性，分别构造两两比较的判断矩阵。构造B1、B2、B3、B4的判断矩阵B，其它判断矩阵同理可得。

3.2.2 确定目标权重

1）计算判断矩阵B中每行所有元素的几何平均值

得到W＝（w1，w2，…，wn）T即为所求特征向量的近似值，这也是各元素的相对权重。在本例中W＝（w1，w2，w3，w4）T＝（0.4668，0.2776，0.1602，0.0953）T。

3）计算判断矩阵的最大特征值λmax

计算判断矩阵B的最大特征根为

3.2.3 一致性检验

计算出判断矩阵最大特征值对应的特征向量（权重）后，需要进行一致性检验：

由表查得RI＝0.89

从计算结果看出，CR＜0.1，这表明上述判断的一致性可以接受，即前面所求得的权重值W＝（0.4668，0.2776，0.1602，0.0953）T是可以接受的。同理，可求得第三层各元素的权重，并分别对其判断矩阵进行一致性检验，这里不再重复，结果，其一致性均可以接受，最后得到各评价指标的权重（见表3）。

表3 登陆作战效能影响因素的权重

以上是评价体系中各指标的权重，下面用模糊综合评价法对其进行评估。

3.3 结合模糊综合评价法评价指标体系

表4 登陆作战效能指标等级评语表

模糊评价法是模糊决策分析的基本方法，其特点是按多项模糊的准则参数对被选方案进行综合评价，再根据综合结果对各备选方案进行比较排序，选出最好的方案［9］。与综合评价有关的有限论域有两种：准则论域和评语等级论域。此处任务为登陆作战，所以根据专家的意见给出了影响登陆作战效能各个指标的模糊评语（见表4）。

由上面计算所得的Ui中的指标权重矢量Ci＝（ci1，ci2，…，ciki），和评语集合V＝｛v1，v2，…，vm｝，由被评价对象相对于各个指标的模糊评语，即Ui×V上的模糊矩阵是

进行如下模糊变换：

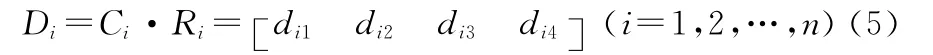
从而得到就每个Ui的评价结果Di。

根据表4所示的数据，我们计算相对于第一层各个指标U 的模糊评语Di（i＝1，2，…，4）。

归一化后计算可得

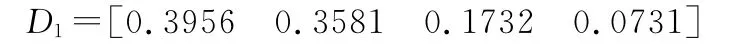
同理可得D2、D3、D4的值分别为

由以上结果可以看出，该登陆作战效能指标体系在火力打击、机动能力、防护能力和保障能力四项评价中，对好和较好的隶属度分别为0.7537、0.6260、0.6074、0.7003，说明上述评价还是比较合理的。评价结果也指出执行登陆作战任务要非常突出火力打击能力和机动能力。在细化的各项指标中，火力压制、装甲和步兵的火力突击能力以及海上机动能力又起着非常重要的作用［11］。