复杂舰载装备系统维修决策分析＊

全文彬 彭鹏菲 黄傲林 卞鸿巍

（海军工程大学 武汉 430033）

1 引言

上世纪60年代开始逐渐发展起来的维修决策建模和分析技术是运筹学和可靠性工程的重要分支，目的是用解析手段或计算机模拟的方法，在各种维修策略下，寻求最佳的更换间隔期或者其他维修活动参数，使得部件或系统单位时间内期望费用最少、可用度最大或满足给定的故障风险等。不同于以可靠性为中心的维修和全员生产维护等定性的维修理念［1］，维修决策建模和分析技术侧重于对系统失效（或劣化过程）以及维修策略进行定量描述，并采用运筹学方法指导维修工作。

Barlow、Proschan和McCall最早开始进行了维修决策建模和分析技术研究［2］。早期对装备的维修主要是故障后维修和定期检修，从20世纪70年代开始，油液分析、振动监测和红外热成像等各种监控技术和监控手段得到了广泛应用，视情维修技术得以推广，维修决策建模和分析问题也日益受到研究人员和工程师的重视［3］。

2 装备维修性分析

2.1 维修分类

过去几十年间，维修、更换和检查已经在诸多文献中被广泛讨论。维修主要被分为两类：修复性维修和预防性维修。

1）修复性维修（Corrective Maintenance）是系统故障发生时进行的维修。根据 MIL－STD－721B，修复性维修意指为使部件恢复到规定的状态而进行的故障后的所有维修工作。修复性维修是一般传统意义上的维修，即系统发生故障则对其进行故障排除的维修活动。

2）预防性维修（Preventive Maintenance）是系统在运行阶段进行的一些维修工作。根据 MIL－STD－721B，预防性维修是指通过进行系统的检查、探测和预防初期故障来使系统保持在一种规定的状态而进行的所有活动。

同时，还可以根据维修程度即维修后恢复到的可运行状态对维修进行分类。如表1所示。

表1 维修分类

1）完全维修：维修可以使得部件恢复到全新的状态，即修复如新。显然用一个全新部件来更换故障部件也是完全维修。经过完全维修后部件的寿命分布和故障率都和全新时刻的一样。对发动机进行大修就是一次完全维修的例子。

2）最小维修：维修使得系统的故障率恢复到它失效前一时刻的状态，这就叫做最小维修。此概念最早由Balow和Proshan提出，经过最小维修后系统的运行状态被称为修复如旧。例如更换汽车上漏气的车胎和更换发动机上坏掉的风扇皮带对于整个系统来说就是最小维修。因为经过这样的维修后整体的故障率并没有发生变化。

3）不完全维修：经过维修后系统的状态没有变成全新，但是比故障那一刻的状态要年轻，这样的维修活动叫做不完全维修。通常情况下，假定不完全维修使得系统的状态介于完全如新和完全如旧之间的某个状态。例如对发动机进行适当的调试就是一种不完全维修，因为调适后发动机并不会恢复到全新的状态而是状态有很大的改进。很显然，不完全维修包含了普通维修中的两种极端情况：最小维修和完全维修。

4）较差维修：经过维修后使得系统的故障率和实际年龄都有所增加，但系统还不至于瘫痪，这样的维修活动称为较差维修。它令系统的运行环境比故障那一刻还要糟糕，这往往可能是由于维修不当所造成的状态变差。

5）最差维修：使得系统失效或者瘫痪的一种维修活动。

在维修过程中对失效部件只进行了部分维修、找错了维修部件或者对故障部件进行维修时损伤到其他部件，都有可能会导致不完全维修和较差维修等情况发生。

2.2 换件策略下备件需求分析

在费用效率均衡的原则指导下，对于单价较低、相对简单、复杂程度较低的装备，一般采用换件维修策略，即故障后立即用备件将故障件换下，显然这是一种完全维修。在此种策略下，根据装备的分类、寿命的分布类型及其适用范围，我们可以确定备件的计算模型，从而确定备件的数量。下面以寿命服从指数分布的装备为例，进行备件需求分析。

指数分布的函数为R（t）＝e－λt，其中故障率（也称失效率）λ为一常数，即系统呈现无记忆性，对于这类装备修复性维修和换件维修具有相同的效果，即系统“修复如新”。更新过程被广泛运用于此类装备的维修建模分析。在时间为t的任意范围内，备件需求数量满足期望值为λt的泊松分布。

当初始备件数量为s时，备件满足率为

因此，可以根据备件满足率P来确定装备的备件存储量（其中N为装备中某部件的实际用数）。

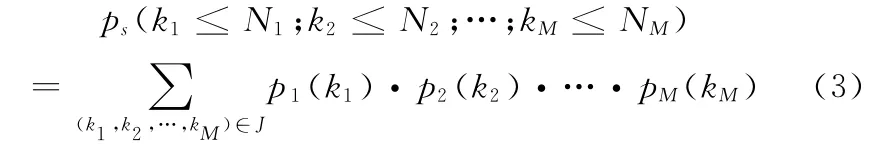
pi（ki）表示第i个部件在规定时间t内备件需求量为ki的概率。可以证明：

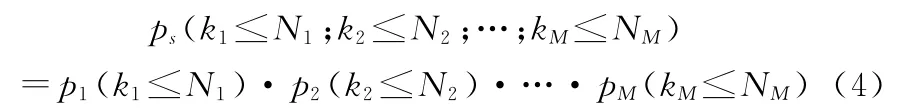
对于寿命服从正态分布的装备，其备件需求计算方法可描述如下：

若已知正态寿命件均值为E，标准差为δ，更换周期（部件故障后，能够得到该件的时间）为t，需要备件时能得到备件的概率P条件下，单项（装备中需用该部件，但只有一个）备件需求量SN表达式为

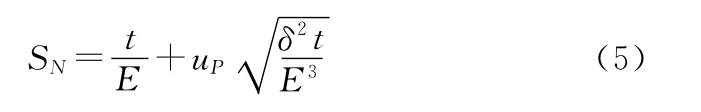
2.3 劣化系统维修策略分析

针对退化系统的各种维修策略，很多文献进行了讨论，其中关于系统的维修策略和最优维修问题的研究大致可分为有状态监测设备和没有状态监测设备两大类。对于没有监测装置的系统，可以当作只有工作和故障两个状态的情况处理，其维修策略：1）对系统作定期（或成批）更换以及定期小修［4］；2）通过对故障时间的预测进行计划维修［5］。对有状态检测装置系统的维修策略主要针对多状态退化情形，通过监测设备跟踪，确定系统任意时刻的状态。根据不同的最优准则，基于状态观测采用恰当的维修策略，这方面也有较多文献［6～8］。对系统进行状态监测后，得出的最优维修策略常常优于定期的计划维修策略，但要观测系统的状态可能要花费很多费用，相应的模型也非常复杂，不易求解。

对于单位造价高、功能结构复杂的装备系统，实际使用中我们一般趋向于采用一种维修策略使得其长期运行的费用率维持在较低水平。当此类装备发生故障时，我们一般先对其进行维修，由于装备的复杂程度较高，一般很难修复如新，“不完全维修”模型很好地描述了此类系统的实际运行过程。系统经过多次维修后性能不断劣化［9］，系统修理后的工作寿命越来越短，系统的维修时间来越长，最终系统不能再工作。

对于劣化系统较常采用的维修换件策略为：P（N）、P（T）、P（N，T）。其中P表示Policy，下面分别对每种策略进行说明。

P（N）：当系统发生故障时对其进行维修，当故障次数达到N时不再对其维修而进行更换；

P（T）：当系统发生故障时若寿命大于T则进行更换，否则对其进行维修；

P（N，T）：当系统故障时寿命大于T或者故障次数累计达N则进行更换，否则对其进行维修。

以P（N）为例，系统在一个换件周期内的运行时序如图1所示。其中Xi，Yi分别表示为第i－1次修后工作时间和第i次维修所需时间。

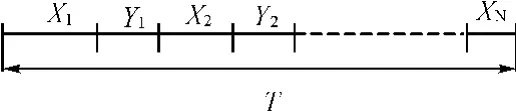
图1 系统周期内运行时序图

3 复杂舰载装备系统维修决策模型

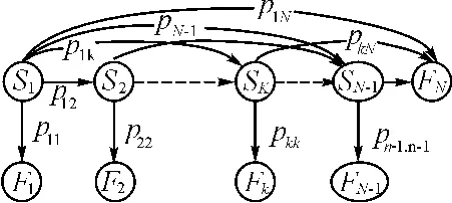
图2 某复杂装备系统运行周期时序图

现代舰载装备系统复杂程度高，保障难度大。装备系统在其寿命周期内一般呈劣化态势，根据前面的介绍假设一个劣化系统有S1，…，SN－1个工作状态和F1，…，FN－1个中间故障状态，还有FN这样一个最终故障状态，S1表示系统初始状态，系统周期内的运行情况如图2所示。

假设系统在状态Si下的平均工作时间为λi，然后以概率pii进入中间故障状态Fi，以概率pij进入工作状态j（i≠j），或者最终故障状态FN（j＝N），其中：

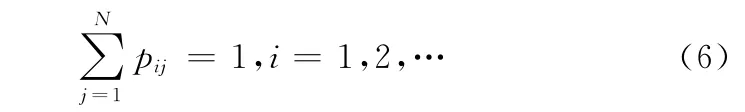
由此可见，系统的劣化过程是一个半马尔可夫过程，状态空间S＝｛S1，…，SN－1，F1，…，FN｝。不妨设维修时可采用的决策集为｛Af，Ar｝，其中Af表示通过不完全维修将系统恢复至故障前状态，即将系统由状态Fi恢复至Si，平均修复时间为μi，维修费用率为fi，其中i＜N。Ar表示换件维修，即对系统进行更换，更换耗时为固定时间τ，固定费用c。记Ai为当系统处于状态Fi时可采用的维修策略，显然有：

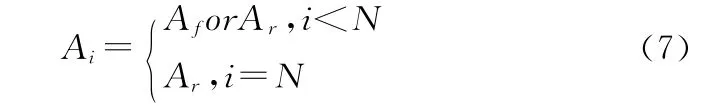
设系统处于故障状态F1，…，FN下对应的维修策略为A＝｛A1，A2，…，AN｝。令TA（Si），TA（Fk）分别表示系统从初次进入工作状态Si或故障状态Fk直到下次替换新系统完成的平均时间。CA（Si），CA（Fk）分别表示上述两个时间段内的平均期望维修费用。则有下述递归方程：

1）当Ai＝Af（1≤i＜N）时

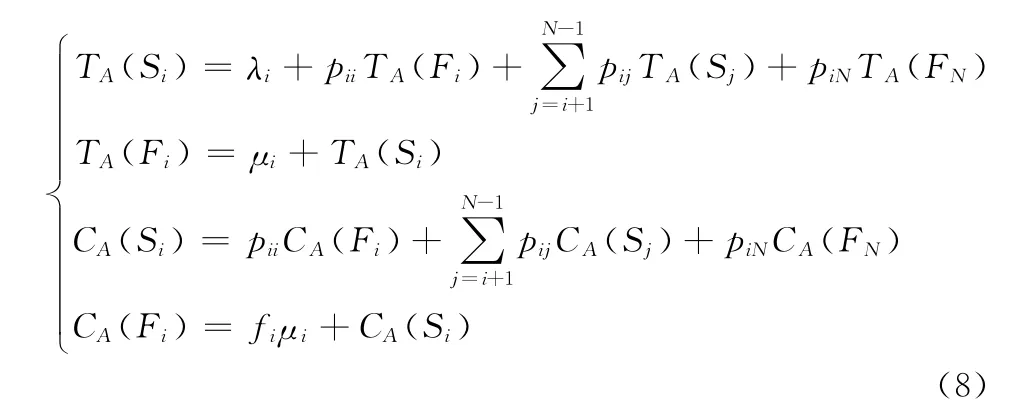
2）当Ai＝Ar（1≤i≤N）时

边界条件为

则最优决策形如A＊＝｛A＊1，A＊2，…，Ar｝使系统长期运行费用率最低，设为g＊，则应有：

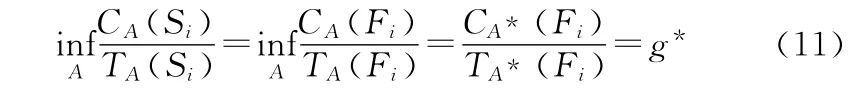
由式（1）～（4），我们运用半马尔可夫决策过程的策略迭代算法［10］进行求解，步骤如下：

1）给定初始策略A（0），其中＝Ar

2）初始任选一个状态Fs（1≤s≤N），令VA（Fs）＝0

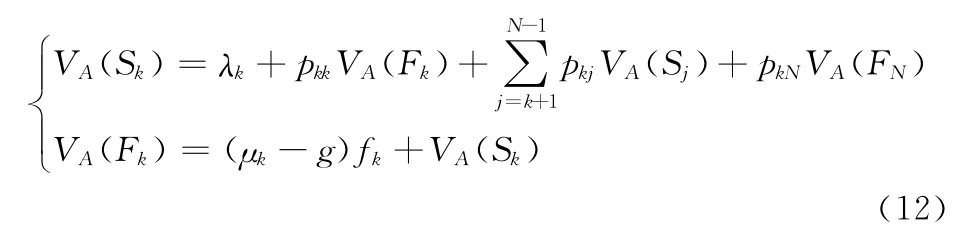
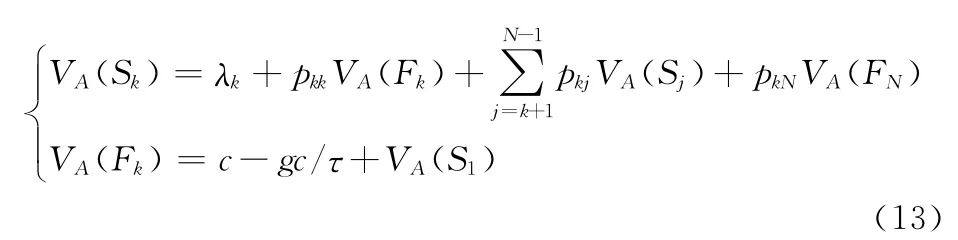
解方程（5）（6）得唯一解｛g（A），VA（Fk）：k＝1，2，…，N｝

3）利用上述结果在每个故障状态Fk（1≤k≤N－1）下，令｛VF｝为该故障状态下，采用不同维修策略可能得到的所有VA（Fk），取其中最下者对应的维修策略，即Ak（1）＝AforAr，最后得出新的维修策略A（1）。

4）如果A（1）＝A（0）算法结束，否则用 A（1）代替 A（0）回到2）重新计算

4 算例

假设某劣化系统有五个不同的工作状态S1，S2，S3，S4，S5和六种故障状态F1，F2，F3，F4，F5，F6，其中前五种故障状态可修，第六种故障状态不可修。不同状态之间的转移概率矩阵如下：

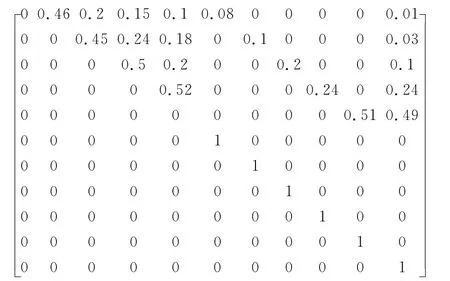
不同工作状态下的平均工作时间为：λ1＝60，λ2＝55，λ3＝45，λ4＝30，λ5＝16，前五种可修故障状态下的维修平均时间和维修费用率分别为：μ1＝1.5，f1＝100；μ2＝1.7，f2＝120；μ3＝2，f3＝140；μ4＝2.5，f4＝180；μ5＝3.5，f5＝230更换固定耗时τ＝10，费用c＝900。

令初始 策略 A（0）＝｛Af，Af，Af，Af，Af，Ar｝，且 VA（F3）＝0，则按照前述迭代算法的步骤得到最优策略为：A（0）＝｛Af，Af，Af，Af，Ar，Ar｝，即当系统处于第5类故障状态时将不再进行维修而是直接更换。从上面的讨论可知影响最优维修策略的主要参数有系统的状态转移概率、不同状态下的维修时间和费用率以及装备本身的价值等。

5 结语

劣化系统是舰载装备中较常见的一类系统。对于此类系统，由于其构成复杂，系统在寿命周期内有多种状态，呈现阶段劣化的特性。对于此类装备传统的维修方式往往忽略了系统劣化的阶段性而采用了统一的故障后维修的方式，当不能维修时进行更换，导致长期维修费用率一直处于高位水平。本文针对劣化系统的特点采用半马尔可夫过程对其维修过程进行建模，给出了在最优维修策略的一般迭代算法。在本文分析结果的基础上可以根据系统的状态转移概率、维修时间、费用等因素制定合理的维修策略，大大降低了维修费用。该方法对于加强装备维护、降低装备运行成本具有指导作用，对装备的备件需求分析也具有一定的参考价值。

［1］贾希胜.以可靠性为中心的维修决策模型［M］.北京：国防工业出版社，2007.

［2］Dekker.R，Application of maintenance optimisation models：a review and analysis［J］.Reliability and System Safety，1996（51）：229－240.

［3］Mobley.R.K.An introduction to predictive maintenance［M］.second edition.Elsevier Science，New York，2002.

［4］Sheu SH，Yeh R H，Lin Y B.A bayesian perspectiveon age re－placementwith minimal repair［J］.Reliability Engineering and System Safety，1999，65（1）：55－64.

［5］Canfield R V.Cost optimization of periodic preventive maintenance［J］.IEEE Transactions on Reliability，1986，35（1）：78－81.

［6］Kallen M J，van Noortwijk JM.Optimalmaintenance decisions under imperfect inspection［J］.ReliabilityEngineering and System Safety，2005，90（2／3）：177－185.

［7］DeliaM C，RafaelP O.A maintenancemodelwith failures and inspection followingMarkovian arrival processes and two repair modes following Markovian arrival processes and two repair modes［J］.European Journal of Operational Research，2008，186（2）：694－707.

［8］CastanierB，GrallA，BerenguerC.A condition－based maintenance policy with non－periodic inspections for a two－unit series system ［J］.Reliability Engineering and System Safety，2005，7（1）：109－120.

［9］Lam Yeh，ZHANG Yuan－lin.A geometric－process maintenance model for a deteriorating system under a random environment［J］.IEEE Transactions on reliability，2003，52（1）：83－89.

［10］Tijms H C.Stochastic Modeling and Analysis：A Computational Approach［M］.New York：John Wiley＆Sons，1986.