复杂军事物流网络的配送路径优化研究＊

陈 晔 张勇明 赵金超

（海军工程大学管理工程系 武汉 430033）

1 引言

物流网络是一个与我们的生活、工作、社会经济环境密切相关的复杂大系统。应用复杂网络理论分析物流网络拓扑结构的复杂性，是研究复杂物流网络的关键所在，也是物流网络研究的基础理论问题之一［1～4］。

随着信息化程度的提高，军事物流体系也实现了信息化、网络化，例如装备物资器材的物流网络，也属于物流网络的一种，但是其运行效率受到多种因素的影响，并具有以下两个显著特点：一是自主性、选择性，该物流网络不仅具有与其它物流网络相似的拓扑特性，而且具有不同于其他网络的显著特点，这些特性要深入分析拓扑结构，对物流网络的承载能力及物流路径的优化进行研究；二是适应性和动态性，该物流网络由于外部作用的驱动或内部因素的作用，网络的拓扑结构不是固定的、成熟的，所以需要从整个网络系统角度出发，对物流网络的节点及节点的物流特性进行分析与合理规划和管理，以达到有效缓解物流配送瓶颈的目的。

本文以装备物资器材物流网络为研究对象，将仓库抽象成节点，运输的公路、铁路、航空线路抽象成边，随着节点和边的数量和连接越来越复杂，可以使用复杂网络理论来分析该军事物流网络。首先建立该物流网络拓扑结构模型，分析其保障功能区分，然后运用启发式算法对配送路径进行优化，最后结合保障实例给出了最佳的配送路径方案。

2 复杂军事物流网络建模及特性分析

这里以装备物资器材的物流网络为例，将仓库所在地抽象成节点，运输的公路、铁路、航空线路抽象成边，为了便于建模和仿真计算，保证网络中节点和边相互存在的合理性，需要作出如下假设：

1）国内铁路、航空、公路可以连接任何一个国内节点，但不一定直接连接；

2）部分交通枢纽开通航空航线，且两两直接相连。

根据以上假设，形成装备物资器材复杂物流网络的拓扑图，见图1。

图1中圆圈代表仓库所在地，其中大的圆圈代表开通航空航线的枢纽，小的圆圈代表使用公路、铁路运输的枢纽，连线代表运输的路径。该图中共有23个节点和45条边。

分析该装备物资器材物流网络的特性，具有两个显著特点：1）网络的增长性，该物流网络在运行过程中，随着保障任务的变化，网络中的节点数量不是一成不变的，会有节点的增加或者减少；2）优先粘贴性，在保障任务运行中，新加入节点与网络中已经存在的关键节点（如国内交通枢纽等）优先粘贴。这两个特性，可以用无标度网络（scale－free）来描述。

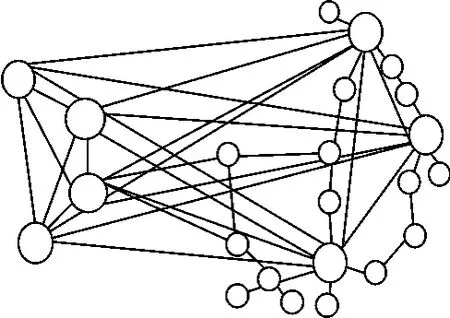
图1 装备物资器材物流网络拓扑图

3 基于启发式算法的复杂军事物流网络路径优化

3.1 启发式算法描述及仿真结论

本文运用近期提出的一种启发式算法［5～8］，优化该复杂物流网络的路径来解决网络的拥塞问题，算法的核心是通过合理分配连接之间的权重来减小或避免信息量过载。但是以上算法没有考虑节点的等待时间（或者信息处理时间）而造成的时延，缺点是网络中关键节点会高度拥挤，最终会导致网络分裂成几个互不连接的网络。文献［9］提出使用动态路径协议（当网络发生拥塞时以数据包的插入率来优化），来避免关键节点引起拥塞以改进网络的容量。

提出的启发式算法，是通过调整网络中最大介数的大小，以改善网络的路径结构，最终达到提高网络信息容量的目的。

为便于比较，本课题使用文献［9］中的scale－free网络模型（网络节点数N在25～1600之间）来描述该算法。假设所有节点在同一时间步长有相同的数据包流量，每个节点在同一时间步长同频率的插入r个新的数据包，数据包的目的地在剩下的N－1个节点中随机选择。

对于给定的路由表，从源节点s到目标节点t经过节点i的数据包数量这样计算：

首先给源节点s分配权重l，然后沿着t→s的路由表，每一个节点的权重平均分配在其前者上，然后再增加其前者的权重。那么，从源节点s经过给定节点i的平均数据包数为

当达到临界平均插入率rc后网络发生拥塞，rc由公式（1）给出：

其中，Bmax是网络中节点的最大介数。

为了达到最优路径，Bmax应该最小。本文提出的优化算法通过增加最初空闲节点的流量来降低经过最初繁忙节点的流量，这样介数分布会变得更加狭窄，最终会重塑网络的介数结构。

3.2 仿真分析

3.2.1 四种路径协议

文献［9］中提到的三种路径协议，加上本文提出的最优算法路径协议，比较和其他三种算法的优劣。四种路径协议分别是最短路径协议（用SP表示），最优算法（用OR表示），有效路径协议（用ER表示），hub失效协议（用 HA表示）。

3.2.2 仿真结论

1）四种路径协议下〈Bmax〉、〈Bavg〉与网络大小N 的相关性

针对图1构建的装备物资器材复杂物流网络，运用Matlab－Simulink仿真工具，仿真〈Bmax〉（最大介数的平均值）、〈Bavg〉（平均介数的平均值）与网络中节点数N之间有幂率相关性。这里仿真比较四种路径协议的优劣。

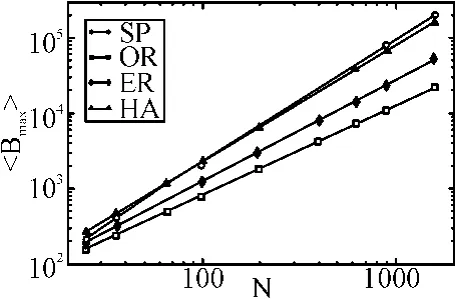
图2 四种路径协议下网络节点数N与〈Bmax〉之间的关系

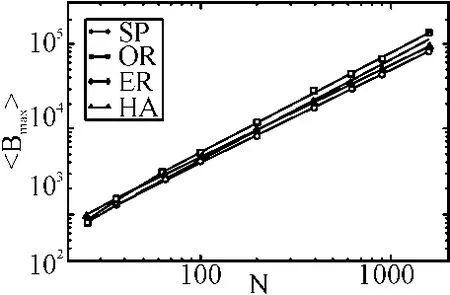
图3 四种路径协议下网络节点数N与〈Bavg〉之间的关系

其中：SP表示最短路径协议，OR表示最优算法，ER表示有效路径协议，HA表示hub失效协议。

表1 〈Bmax〉、〈Bavg〉与网络节点数N之间对应的幂率指数（估计误差为2σ）

从图2～3可以看出，OR算法较其它三种算法优秀，结果使Bmax、Bavg之间的差值最小。最终，〈Bavg〉OR－〈Bavg〉SP（大于〈Bavg〉ER－〈Bavg〉SP或者〈Bavg〉HA－〈Bavg〉SP）差值保持很低，而且〈Bavg〉OR与网络大小N 的幂率指数稍高于〈Bavg〉SP对应的指数（详见表1对应的数据）。

2）Bmax与迭代次数的函数关系

本文提出的启发式算法，最大介数做为迭代次数的函数并不是单调的，但是表现出递减的趋势，最终最大介数限制在一个较窄的范围内。这里仍以图1构建的装备物资器材复杂物流网络为例，运用 Matlab－Simulink仿真工具，仿真出Bmax与迭代次数之间的函数曲线（见图4），这样可以帮助我们找到对应的全局最小Bmax。

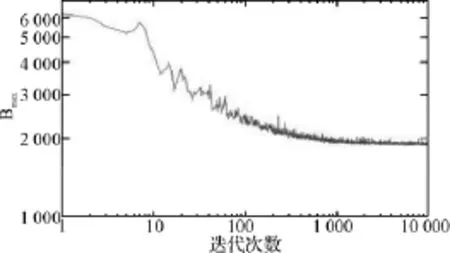
图4 Bmax与迭代次数之间的函数曲线

3）优化前后介数分布情况比对

该算法使用给定路由表的网络平均介数Bavg提供了最大介数的下限，只有当优化路径使得所有节点有相同流量时才能达到该下限。网络的最大介数和平均介数之间的差距，同样也是衡量介数分布范围的尺度。而且当最短路径上的权重都设置为1的时候，使用任意路由表计算的平均介数会达到其下限。由于任何最短路径的变化会导致更长路径，这样会增加整个网络的介数，显然一个好的优化算法，应该具备以下两种特征：

（1）最大介数和平均介数差最小；

（2）同时保持使用最佳路由表和最短路径两种方法计算的平均路径的差尽可能小。

这里针对图1的网络，运用 Matlab－Simulink仿真工具，仿真其介数分布，通过控制介数的分布，来优化网络的路径结构。

图5给出了经过优化算法前、后装备物资器材复杂物流网络介数分布图。从图5可以看出：优化前大多数节点有较低的介数，其中有一小部分节点介数分布在宽广的范围，经过启发式算法优化后，所有节点的介数被限制在一个狭窄的范围内，尤其是分布上限被严格限制，大多数节点统一分布在一个范围内，其上限有很明显的峰值而后有显著的递减趋势。这验证了该算法可以明显减小最大介数和平均介数的差值，以优化网络的结构。

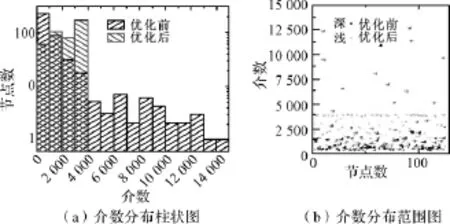
图5 优化前、后网络中介数分布图

4 仿真实例分析

这里假设有以下四种保障任务，需要从某仓库调出某型器材配送到某港口，具体任务见表2。

表2 装备物资器材复杂物流网络保障任务

根据优化算法，将每类补给途径的补给时间和补给成本假设为权重l1，l2，单位分别以小时和万元表示。根据以上考虑，制定出补给路线的路由表（见表3）。

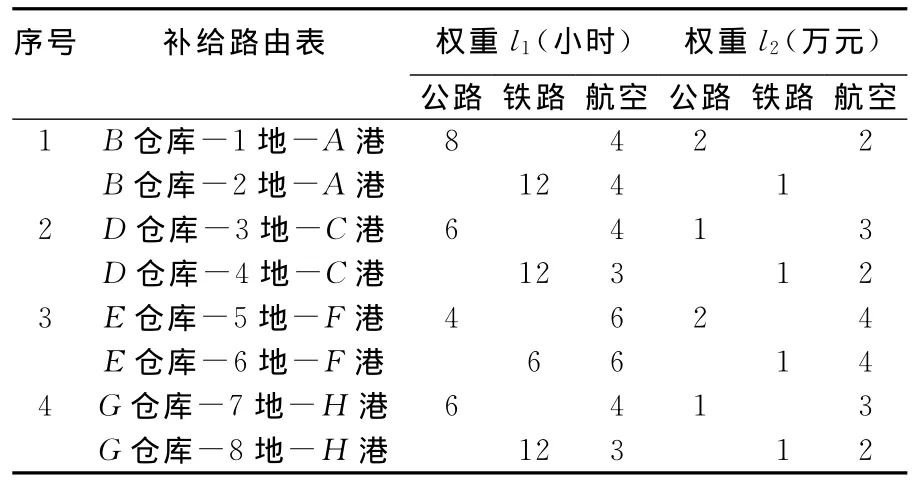
表3 装备物资器材补给路由表

根据表3和前面提到的启发式算法，可以计算出每项补给任务补给路径的对应值（见表4）。

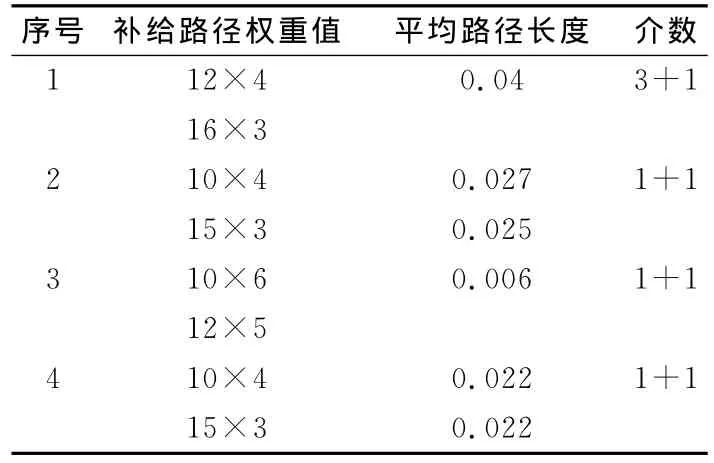
表4 装备物资器材补给路径对应值

考虑到战时装备物资器材物流网络会因为保障任务的增加而变得繁忙，某些节点会因为出入库物资器材过多而产生网络拥塞，这里假设图6中节点2、5出现拥塞，结合本文使用的最优算法路径协议和节点的保障任务分工，得到最终的优化补给方案，见表5。

图6 装备物资器材物流实例图

表5 优化后的装备物资器材补给方案

5 结语

本文以装备物资器材军事物流网络为研究对象，建立了其拓扑模型，提出运用启发式路径优化算法，并通过Matlab－Simulink对复杂参数的仿真，结合四个保障实例，提出了最佳的保障补给方案，该优化方法为提高军事物流网络的保障效率提供了一定的理论参考。

［1］李慈.基于复杂系统理论的配送网络优化研究［D］.西安：西北工业大学硕上学位论文，2006.

［2］黄建华.快递网络的复杂性及鲁棒性分析［J］.西南交通大学学报，2009（12）：98－102.

［3］牛永亮，王金妹.物流配送车辆路线求解算法［J］.交通运输工程学报，2006（6）：83－87.

［4］王佳，池洁，王勇.物流中配送路线选择的优化分析［J］.物流科技，2009（1）：18－20.

［5］M.Ericsson，M.G.C.Resende and P.M.Padalos，Probability distribution of solution time in GRASP：An experimental investigation［J］.Journal of Combinatorial Optimization，2002（6），299－333.

［6］B.Fortzand M.Thorup，Progessive image compression for a power constrained channel［J］.IEEE Journal on Selected Areas in Communications，2002（20）：4.

［7］Gabrel V，Knippel A，Minoux M.A comparison of heuristics for the discrete cost multicommodity network optimization problem［J］.Journal of Heuristics，2003（9）：429－445.

［8］D.Allen，I.Ismail，J.Kennington and E.Olinick，Wireless Network Design：Optimization Models and Solution Procedures［J］.Journal of Heuristics，2003（9）：375－399.

［9］B.Danila，Y.Yu，John A.Marsh and K.E.Bassler，optimal routing on complex networks［J］.arXiv：cond－mat／0607017.