基于BP神经网络的舰船组合导航算法研究*
2013-10-16白帆孙宁
白 帆 孙 宁
(1.92941部队95分队 葫芦岛 125000)(2.辽宁工程技术大学 兴城 125105)
1 引言
以全球定位系统(GPS)和惯性导航系(INS)构造的组合导航系统是舰船导航中最主要的组合方式。它有效利用了GPS和INS各自的优点进行系统间的取长补短,这种组合能有效减小系统误差,提高系统的精度,而且还可以降低导航的成本。在GPS信号接收正常时,组合导航系统能够提供良好的导航性能。但是载体在恶劣环境下GPS信号会失锁甚至有时会完全丢失,滤波器输出就会发散,系统模型误差会变大使导航性能严重恶化[1]。本文提出用BP神经网络来辅助GPS/INS组合导航系统,既能像模糊系统那样表达近似定性知识,又有神经网络的学习和非线性表达能力。
2 组合导航中的滤波定位模型[2]

图1 INS/GPS组合导航原理图
组合导航系统是把两种或两种以上不同的导航设备或系统以适当的方式组合在一起的导航系统。组合导航系统利用不同导航系统性能上的互补性以获得更好的导航性能,以及更低的系统成本。其中相应的组合方式有,GPS/INS组合导航系统、地形辅助/惯性导航系统、景象匹配/惯性组合导航系统、天文/惯性组合导航系统、罗兰/惯性组合导航系统、多普勒/惯性组合导航系统有关等等。组合导航系统能够克服单个导航系统的不足,提高整个导航系统的导航精度、实时性、提高抗干扰的能力、降低整个系统的造价。所以组合导航系统是导航技术发展的主要方向[3]。
本文采用惯导误差传播模型建立卡尔曼滤波状态方程,组合方式为开环式。滤波器模型如下:

其中:Xu= [Δλ,Δφ,Δh,ΔVe,Vn,Vu,φe,φn,φu,Δt,δ]为状态向量,分别为运动载体的经度误差、纬度误差、高度误差、东向速度误差、北向速度误差、天向姿态误差角、北斗接收机钟差和频漂。A为系统矩阵,阶数等于状态向量Xu的维数,H为观测矩阵。
3 BP神经网络
BP(Back Propagation)神经网络是一种神经网络学习算法,全称基于误差反向传播算法的人工神经网络,由信息的正向传播和误差的反向传播两个过程组成[4]。BP神经网络的拓扑结构是神经网络最为基础的一部分,图2显示了一个典型的三层BP神经网络结构[5],其中:
输入层:输入向量x=(x1,x2,…,xn)T;隐含层:输出向量y=(y1,y2,…,ym)T;
输出层:输出向量o=(o1,o2,…,ol)T;期望输出向量d=(d1,d2,…,dl)T;
输入层到隐含层之间的权值v=(v1,v2,…,vm)T;

图2 三层BP神经网络结构图
隐含层到输出层之间的权值矩阵w=(w1,w2,…,wl)T。
BP神经网络的学习过程主要由信息的正向传播与误差的反向传播两个过程组成[6]:
第一阶段:正向传播时,输入样本从输入层传入,经各隐含层逐层处理后,传向输出层,得到网络的输出结果。

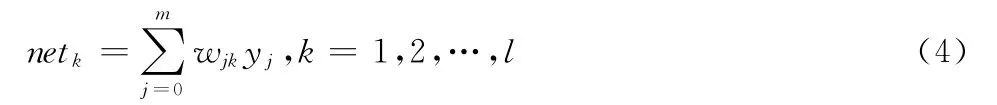
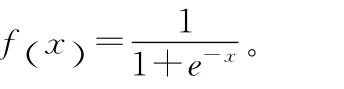
第二阶段:若输出层的实际输出O与期望输出d不符,则转入误差的反向传播阶段,通过误差调节权值。梯度下降法的目的就是使实际输出和期望输出的误差E沿下降速度最快的方向(负梯度方向)减小,所以采用负梯度方向调整权值:
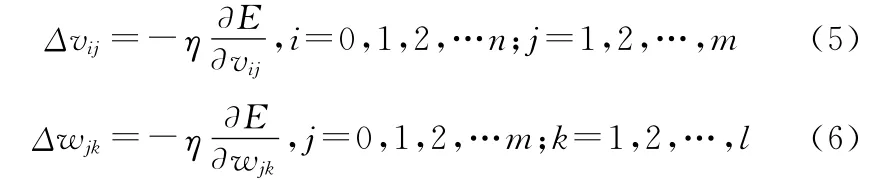
其推导过程如下:

那么,新的权值分别是(η为学习因子):
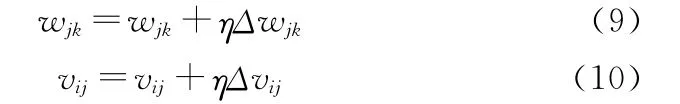
在新的权值下,再次输入样本进入正向传播阶段,计算误差为E或δ,若误差没有达到容许范围,那么进入误差反向传播阶段,继续调整权值[7]。这样第一阶段和第二阶段一直构成一个有机的循环,此过程一直进行到网络输出的误差减少到可以接受的程度,或者预先设定的学习次数为止。
4 基于BP神经网络的组合导航定位算法
结合神经网络和卡尔曼滤波,主要是从补偿的角度,利用神经网络的映射逼近能力和自学习能力修正了卡尔曼滤波的结果,提高滤波精度。BP神经网络考虑了现实环境的动态变化对系统模型造成的随机的干扰影响,通过预先确定的神经网络结构和初始参数,根据足够精度的样本对前向神经网络进行训练,以确定神经网络的各个参数[8]。在卡尔曼滤波器执行导航估计时,将确定的能直接影响导航估计误差的参数作为神经网络的输入,通过实时执行神经网络输出卡尔曼滤波估计的误差来校正卡尔曼估计[9]。
针对惯性/GPS导航系统设计滤波器,将GPS接收机的输出位置和速度信息与惯导输出的相应信息作差得到测量方程。
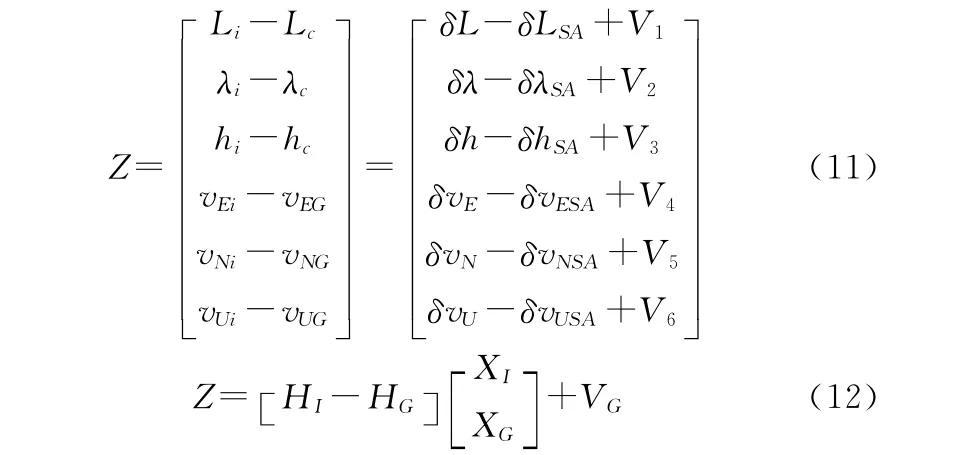
BP神经网络的组合导航定位的算法如下:
1)创建两个BP神经网络,在时间更新预测部分使用一个BP神经网络学习前一个状态和下一个预测状态之间的关系,网络的输入为预测状态与前一个的卡尔曼滤波增益,输出为期望预测状态与预测状态的差[10]。在测量更新部分,使用另一个BP神经网络学习卡尔曼滤波结果与真实结果的误差,网络的输入为卡尔曼滤波的状态参量和卡尔曼滤波增益,输出结果和真实值之间的误差。
2)分别对这两个BP神经网络进行初始化,设定初始的权值和阈值,并通过网络进行训练。
3)开始执行卡尔曼滤波。
4)开始执行两个BP神经网络,实时地分别在时间更新预测部分及测量更新部分修正预测结果。
5)计算误差函数,然后计算反传的误差变化以及各层的权值与新权值结合卡尔曼滤波结果及其由第二个BP神经网络给出的误差,就可以得到BP神经网络修正卡尔曼滤波之后的改进结果。
6)将训练后的值取代卡尔曼滤波的估计值。
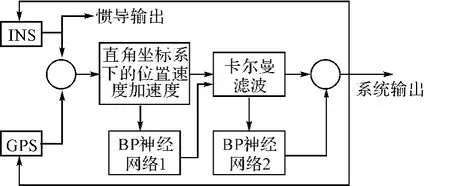
图3 基于BP神经网络动态滤波算法图
5 仿真与分析
模拟海上航行的船舶,对其速度数据进行跟踪,截取一段运动数据进行分析。其导航系统的方程因机动运动有所变化引起测量方程有误差。选取线性神经网络输出结构,将两个BP神经网络嵌入到滤波器中,采用LMS算法进行调整[11],仿真结果如图5所示。

图4 速度测量值与估计值的比较曲线
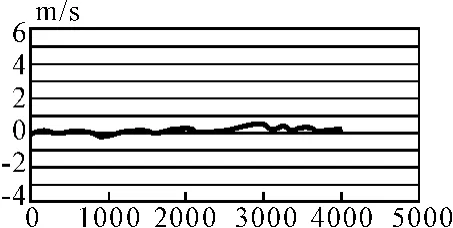
图5 组合滤波后误差信号
从图5中可以看出用神经网络辅助的卡尔曼滤波对速度的估计与实际运动的曲线基本一致,经过长时间的运动也不会产生巨大偏差,证明滤波器没有产生发散现象,使组合导航的精度大大提高。
6 结语
通过仿真可知,该算法既考虑了现实环境的动态变化对系统模型的影响,又融合了神经网络的自学习性和自适应性,使其具有自适应能力以应付动态环境的扰动。仿真结果表明,提出的BP神经网络的组合导航算法,可以显著改善卡尔曼滤波器的性能,提高组合导航的精度。
[1]徐绍铨,张华海,杨志强,等.GPS测量原理及应用[M].武汉测绘科技大学出版社,1998:96-101.
[2]秦永元,汪叔平.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,2004:71-78.
[3]干国强,邱致和.导航与定位[M].北京:国防工业出版社,2000.
[4]徐丽娜.神经网络控制[M].北京:电子工业出版社,2003:117-125.
[5]张剑湖,叶峰.人工神经网络的模型、特征及其发展方向[J].现代电子技术,2004(12):57-60.
[6]徐丽娜.神经网络控制[M].北京:电子工业出版社,2003:228-241.
[7]刘增良.模糊技术与神经网络技术选编[M].北京:北京航空航天大学出版社,2001:117-125.
[8]王新龙,申功勋,唐德麟.基于最优估计神经网络的惯导系统初始对准研究[J].宇航学报,2002,23(3):34-38.
[9]杨元喜.动态Kalman滤波模型误差的影响[J].测绘科学,2006(1):17-18.
[10]董晓马,张为公.基于改进BP神经网络的车轮定位参数动态测量[J].试验·测试学报,2003(12):31-33.
[11]张守信.航天测量数据处理[M].北京:解放军出版社,1999:52-57.
[12]杨金宝,张昌宏,陈平.基于改进BP神经网络的网络故障诊断研究[J].计算机与数字工程,2012,40(2).
[13]张守信.航天测量数据处理[M].北京:解放军出版社,1999:208-215.
