基于H和μ综合的防空导弹鲁棒控制器设计＊∞

王 垒 王瑞革

（1.解放军91404部队 秦皇岛 066000）（2.解放军92785部队 秦皇岛 066000）

1 引言

防空导弹要攻击来袭的飞机、导弹等超高速大机动目标，在大空域范围飞行过程中，飞行环境复杂，气动参数变化剧烈；导弹处于高空高速、大机动飞行状态，是非线性、时变不确定性，耦合严重的复杂系统。导弹控制器的设计要充分考虑到外界干扰、输入测量噪声和不确定参数随机摄动等影响。

传统的控制器设计能在一定条件下有较好的控制效果，但其鲁棒性能较差［1～2］。文献［3］采用最优控制和经典控制综合的设计方法可以改善自动驾驶仪的鲁棒性能；为提高控制系统鲁棒性能，还可应用线性反馈将模型不确定性限定在一定范围内［4］；文献［5～6］采用μ综合控制克服不确定性参数小范围摄动对系统鲁棒性能的影响，但并未与H∞鲁棒控制进行分析比对。

本文从建立包含有不确定性扰动参数的俯仰通道数学模型出发，分析被控对象的不确定性摄动参数，建模分析舵机随动标称理想模型和输入噪声，分别应用H∞和μ综合控制对非线性、时变飞行条件下俯仰通道姿态控制器进行设计仿真，验证说明了包含模型不确定性因子和干扰噪声的鲁棒控制有较好的动态性能和鲁棒性能，且采用D－K迭代的μ综合控制性能优于H∞控制。

2 俯仰通道数学模型

参考导弹线性化数学模型［7］，建立包含有气动参数、外界干扰、测量噪声等不确定性摄动参数的大气层内防空导弹弹体模型。以俯仰通道为例进行鲁棒控制器分析设计，得到式（1）所示俯仰通道时变、非线性数学模型：

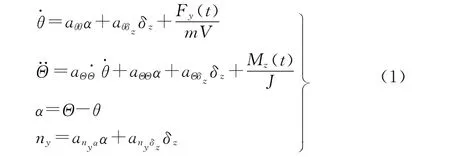
3 不确定性分析

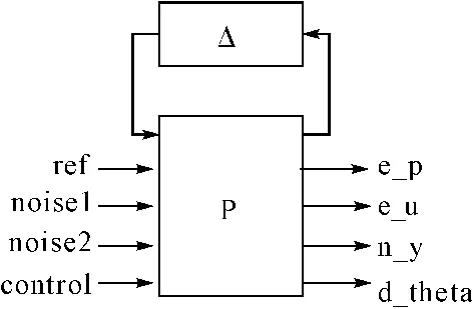
图1 模型不确定性分析

开环系统模型含有14个变量，11个输入和11个输出，见图1。其中输入量ref为参考信号，nosie1，nosie2分别为过载测量噪声和攻角测量噪声，control为控制信号；输出量e＿p，e＿u分别为控制量权重函数和过载权重函数，n＿y为过载输出，d＿theta为舵机响应；不确定部分Δ由七个不确定参数构成［9］，即（aΘΘ，aΘδz，，aθθ，aθδz，anyα，anyδz），限 定 参数扰动范围为±30%，进而闭环系统的不确定性部分可以定义为

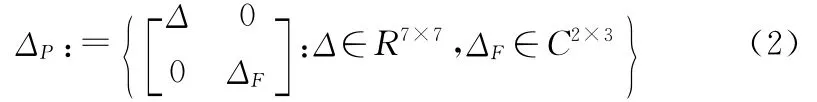
其中Δ为开环传递函数不确定部分，ΔF为系统进行鲁棒控制器设计引入的性能要求部分不确定函数描述。

4 控制器性能分析

4.1 测量噪声分析

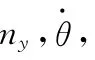
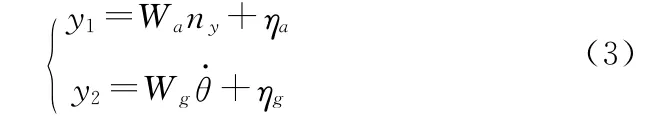
其中Wa为过载测量传递函数，Wg为攻角测量传递函数，有：

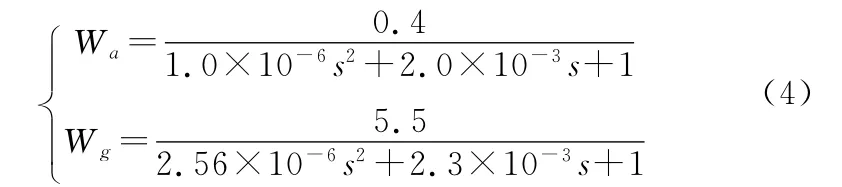
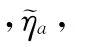
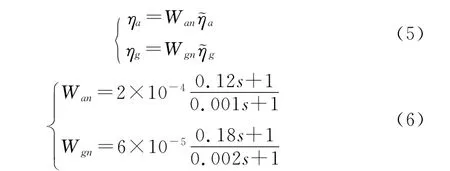
分析可得测量噪声为频率ω的函数，在低频段幅值较小，随着频率的增高而变大，具有高通滤波性。

4.2 控制性能分析

控制器设计的目的是在随机扰动和测量输入噪声存在的情况下，输出过载能够在理想时间内稳态跟踪并保持在过载指令较小误差范围内。

舵机执行机构模型：

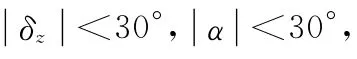
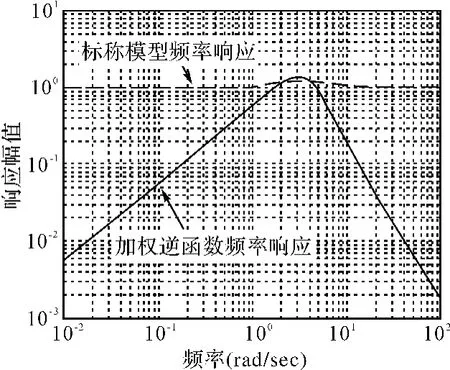
图2 标称模型和性能函数频域响应

5 鲁棒控制器设计

5.1 H∞控制器设计

将系统模型简化为图3所示形式。H∞控制的实质是求解合适的输出反馈矩阵K，使得被控弹体模型P在系统不确定参数理想标准化条件下实现反馈控制。忽略系统内部Δ不确定参数的影响，将其对特征点的数据进行固化、定常处理，只考虑测量噪声˜ηa，˜ηg和输入控制信号r，求解合适的反馈矩阵K，进行H∞控制器设计。

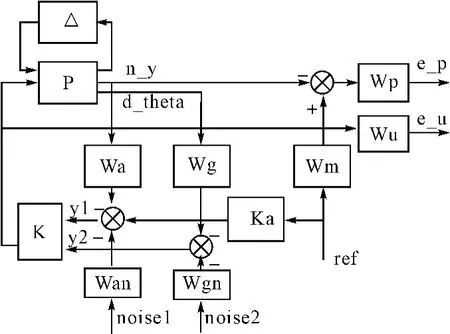
图3 鲁棒控制器闭环结构

5.2 μ综合控制设计

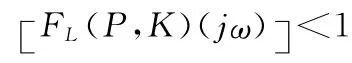
建立图3所示的μ综合控制器设计系统，参考H∞控制器测量噪声和控制信号影响，结合不确定参数Δ：（aΘΘ，aΘδz，aΘΘ·，aθθ，aθδz，anyα，anyδz）部分±30%的扰动，忽略标称等效模型Wm，采用标准D－K算法，可以求解式（2）中不确定对角矩阵ΔP条件下的反馈控制矩阵K。

6 算例仿真

6.1 时域响应分析

算例中弹道平均高度5000m，导弹初始速度Vt0为300m／s，控制时刻速度Vtf为902m／s，攻角α为30°。图4为跟踪控制12g方波信号的响应图，其中H∞控制阶跃响应超调量为25%，响应时间为1.6s，不满足标称系统动态响应时间和超调量的要求；μ综合控制超调量为4.5%，响应时间为0.72s，满足性能要求。由于未考虑被控对象内部不确定性因素影响，H∞控制器性能随ω的增大而变差，超调量增大；舵机跟踪控制指令响应时，在舵机工作性能之内，μ综合控制性能优于H∞控制。

6.2 鲁棒稳定性和鲁棒性能分析

分析比较H∞控制和μ综合控制性能，有H∞控制标称性能参数为0.43258，μ－鲁棒稳定性参数为0.51865，μ－鲁棒性能参数为1.1515，1.1515＞1，此时鲁棒性能欠佳；μ综合控制标称性能参数为0.56257，μ－鲁棒稳定性参数为0.44086，μ－鲁棒性能参数为0.85242，均小于1，满足限制条件。

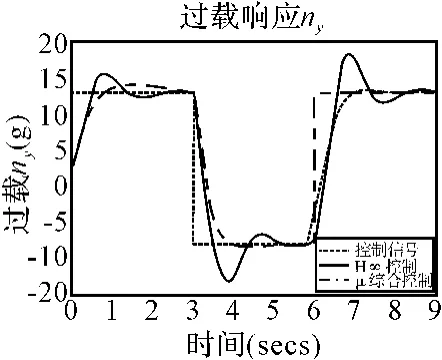
图4 过载响应

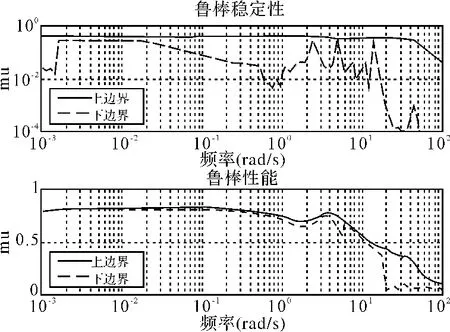
图5 μ综合控制器性能分析

图5为μ综合控制器频域响应，上边沿控制器响应幅值均高于被控模型时域响应幅值。μ综合控制器考虑了摄动的结构特性，降低了控制器的保守性，结构奇异值在所有频段上都小于1，达到了鲁棒性能要求。

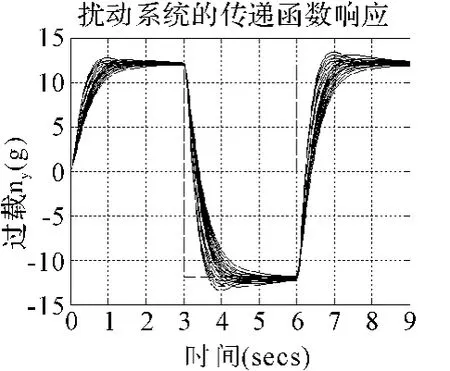
图6 过载扰动响应

图6为导弹平均飞行高度为9000m，不确定参数扰动范围在±30%内时，μ综合控制系统下采样测算64个特征点的过载响应曲线。图中参数扰动范围较大，但跟踪曲线时域响应接近，响应时间和超调量都能够满足系统的鲁棒稳定性能要求，可以通过在有代表性的特征飞行节点处设置控制器参数，完成整个飞行弹道中的过载跟踪控制任务。

7 结语

在复杂飞行条件下建立了包含有测量噪声和不确定参数扰动的导弹俯仰通控制模型，采用频域分析选取合适的标称模型，对输入噪声进行建模分析，考虑不确定参数的大范围摄动，应用H∞和μ综合方法对控制器进行设计分析，验证了鲁棒控制器时域响应的优化性能，且采用标准D－K算法的μ综合方法控制鲁棒性能在不确定参数大范围摄动条件下优于H∞方法，可以保证防空导弹大空域内控制器性能稳定，减少飞行条件剧烈变化时控制器参数的频繁修改设定，提高控制器控制效能。

［1］E.Devaud，H.Siguerdidjance，S.Font.Some control strategies for a high－angle－of－attack［J］.Control Engineering Practice，2000（8）：885－892.

［2］吉礼超，宋贵宝.防空导弹控制方法的研究现状及展望 ［J］.战术导弹技术，2009（3）：54－59.

［3］邢立旦，陈万春，殷兴良.倾斜转弯导弹三回路鲁棒自动驾驶仪设计［J］.系统工程与电子技术，2008，30（10）：1953－1956.

［4］Chanho Song，Sang－Jae Kim，Seung－Hwan Kim.Robust control of the missile attitude based on quaternion feedback［J］.Control Engineering Practice，2006（14）：811－818.

［5］张晓峰，杨军.大攻角飞行导弹控制器μ综合设计［J］.火力与指挥控制，2009，34（10）：125－128.

［6］张举，祝小平.大攻角飞行空空导弹鲁棒自动驾驶仪设计［J］.火力与指挥控制，2010，35（4）：111－117.

［7］刘兴堂.导弹制导控制系统分析设计与仿真［M］.西安：西安工业大学出版社，2006：97－133.

［8］李玉林，杨树兴.先进防空导弹直接力／气动力复合控制关键技术分析［J］.兵工学报，2007，28（12）：1523－1527.

［9］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用［M］.北京：清华大学出版社，2003：64－11.

［10］张成.大机动制导火箭弹控制方法研究［J］.北京理工大学学报，2010（12）：1432－1435.