基于小波分析的柳河地区年降水量和径流量变化规律分析

2013-10-15陈连惠张光锦陈连芹张玉坡

海河水利 2013年2期

陈连惠，张光锦，陈连芹，张玉坡

（1.天津市水文水资源勘测管理中心，天津 300061；2.水利部海河水利委员会，天津 300170；3.天津市水务局大清河管理处，天津 300061）

1 引言

柳河是滦河的重要支流，近年来柳河等地区降水量和径流量的急剧减小，使引滦水源地水资源量发生变化，致使天津市面临城市供水紧张的局面，迫使天津市连续多次实施引黄济津应急调水[1，2]。本次研究通过对柳河地区降雨量、径流量进行统计，分析降雨量和径流量变化规律，为南水北调建成通水之前合理安排天津市城市供水调度方案、科学规划天津市水资源供需配置、支持天津市经济社会可持续发展提供决策依据。

2 计算方法

小波分析法是由Morlet于20世纪80年代提出的一种具有时频多分辨功能的时间序列分析方法，并逐渐被广泛应用，特别是对水文要素时间序列规律的分析[3-7]。小波分析是一种窗口大小固定但形式可变的时频局部化分析方法，具有自适应的时频窗口：高频段时，频域窗口增大，时间窗口减小；低频段时，时间窗口增大，而频域窗口减小。小波函数ψ（t）是指具有震荡特性、能够迅速衰减到0的一类函数，若函数 ψ（t）∈L2（R），L2（R）表示在实数域上平方可积，并且其傅里叶（Fourier）变换 ψ（ω）满足：

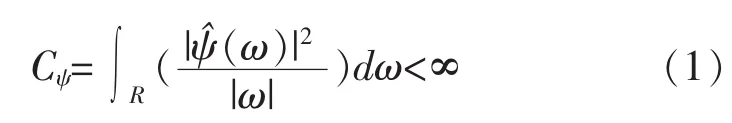
小波母函数经伸缩和平移后派生出一族函数：

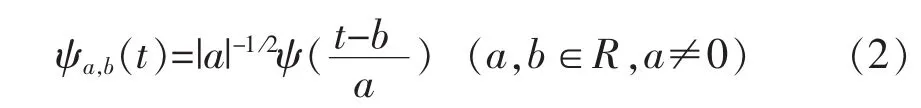
式中：ψa，b为连续小波；a 为尺度伸缩因子；b 为时间平移因子。

若函数 f（t）∈L2（R），则 f（t）可用来表示能量有限的连续时间信号，其连续小波变换如下：

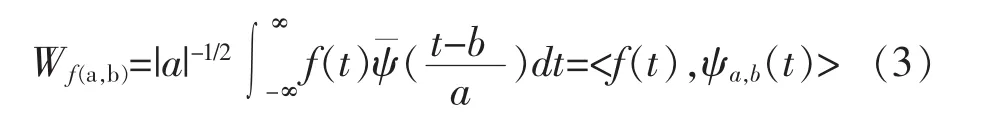
式中：Wf（a，b）为小波变换系数的共轭函数；＜，＞表示内积。

连续小波变换是将连续时间信号f（t）等距映射到二维尺度—时间平面，即a-b平面，其自由度明显增加，从而使得小波变换系数含有很多冗余信息。在实际应用时，常将尺度伸缩因子和时间平移因子离散化：，a0＞0 且 a0≠1，b0∈R，再进行小波变换，以减少小波变换系数的冗余度，则连续小波变成离散小波：

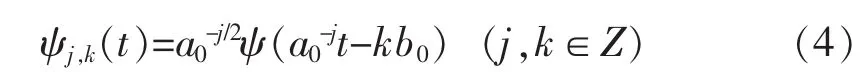
式中：Z为整数。

一维信号f（t）的离散小波变换为：

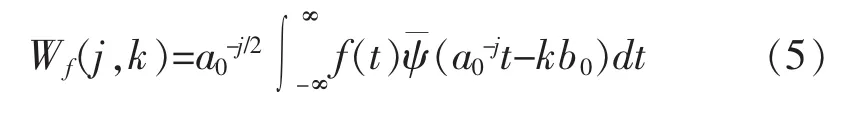
离散小波变换同样能实现窗口的大小固定、形状可变的时频局部化功能。

在对水文时间序列进行小波分析时，通常会寻求一种计算快捷的小波变换算法。其中，Mallat算法是基于多分辨率分析的基础上提出的，适合于正交小波和双正交小波对信号的快速分解和重构，它包括Mallat分解算法和重构算法两部分。

对于一维信号 f（t）∈L2（R），所采用小波尺度函数为 φ（t）、小波函数为 ψ（t），其 Mallat分解算法为：

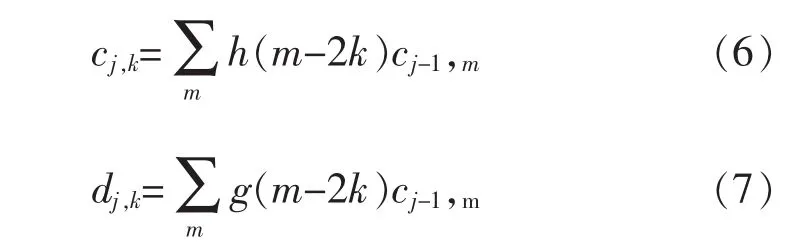
式中：j为分解尺度；k、m 为平移系数；h（n）为分解低通滤波器的冲激响应；g（n）为分解高通滤波器的冲激响应；ci，j为j尺度下的尺度系数，可由下式计算：

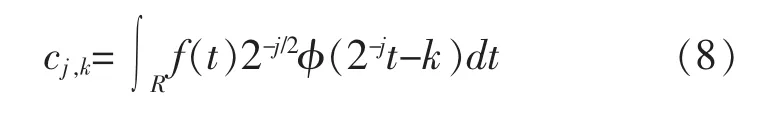
dj，k为j尺度下的小波变换系数，可由下式计算：

这样，随着分解尺度j的增大，信号可以逐级分解下去。重构算法是分解算法的逆过程，Mallat重构算法为：

利用Mallat快速算法对水文时间序列进行小波分解，得到各种尺度下的尺度系数，再对各种尺度系数进行单支重构，得到不同尺度下的低频序列，然后根据水文序列的低频序列进行分析，就可判断水文时间序列的变化趋势。

3 结果与讨论

柳河发源于兴隆县雾灵山东南八拔子，最后汇入潘家口水库，河流长度为137 km，流域面积为1 199.15 km2，河道坡降5.62‰，海拔高度为170～900 m。本次研究以柳河地区为例，基于小波理论分析年降水量和径流量变化规律及相互之间的协同变化规律。

3.1 柳河地区年降水量变化规律分析

对柳河实测年降雨量过程采用小波分解，可得到其近似部分如图1所示。

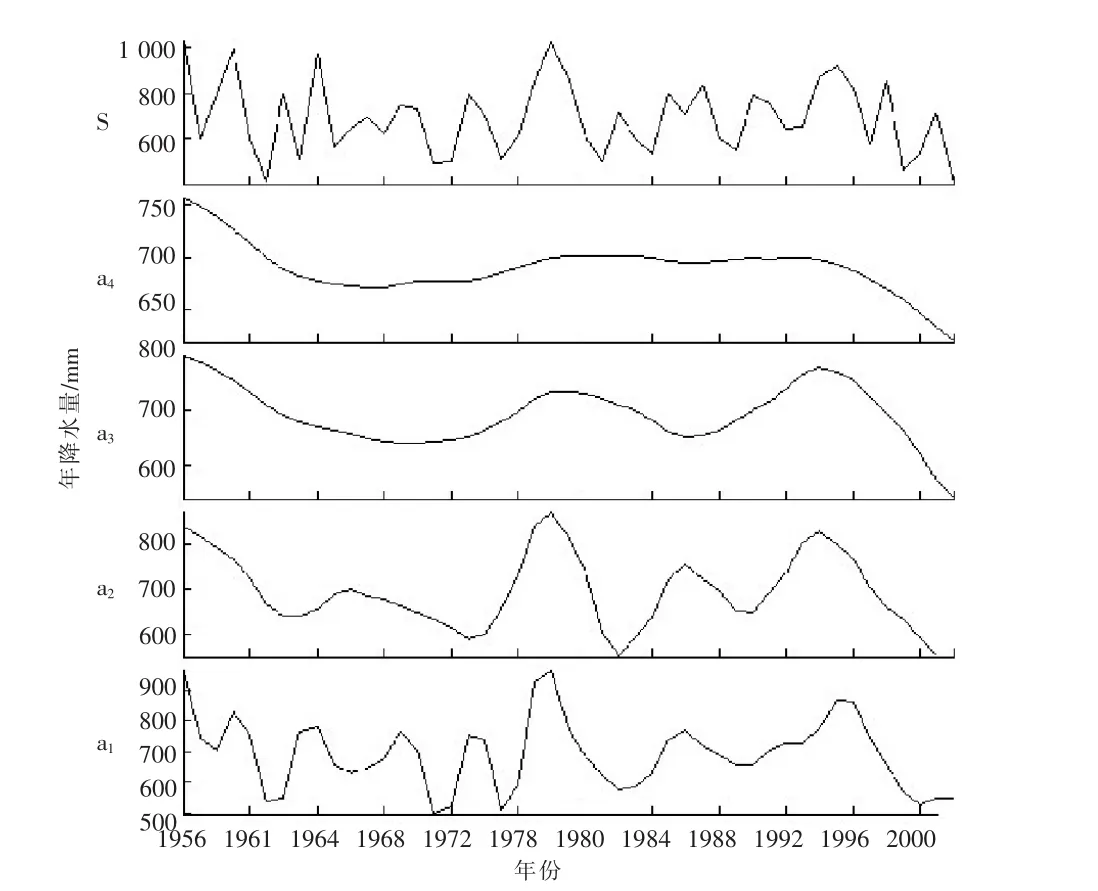
图1 基于小波分析的柳河年降水量变化趋势

图 1 中的 a1、a2、a3、a4是在不同尺度下滤掉了高频信号即忽略了细节部分，反映了年降水量变化趋势。由a2、a3和a4可以看出，该流域的年降水量大致可分为3个阶段：从20世纪50年代中期到20世纪70年代初，降水量逐年减少；从20世纪70年代初期到20世纪90年代中期，降水量曲线比较平缓；从20世纪90年代中期到21世纪初，降水量锐减。

3.2 柳河地区年径流量变化规律分析

对柳河李营站实测年径流量过程采用小波分解，可得到其近似部分如图2所示。

图2 基于小波分析的柳河年径流量变化趋势

由图2中a2和a3可以看出，该站的年径流量大致可分为2个阶段：从20世纪50年代中期到20世纪70年代中期，径流量有逐年增加的趋势；从20世纪70年代中期到21世纪初，径流量先减少后增加，然后锐减。由a4可以看出，柳河李营站年径流量特别是20世纪60年代中期以来，总体呈减少趋势。通过分析计算可以知道，柳河李营站的年径流量变化呈一定周期性，但从1956—2002年长序列整体趋势来看，柳河年径流量呈减少趋势。为进一步分析柳河地区的降水量和径流量之间的相互关系，下面将通过双累计曲线法进行相关关系分析。

3.3 柳河地区降水径流相关关系分析

3.3.1 双累计曲线分析

区域降雨径流关系是区域产流条件的综合反映，通过对其变化规律的分析，可以确定柳河流域产流条件的变化以及对入库径流量的影响。采用1956—2003年流域控制面积内的平均降水量、实测径流量、用水量和柳河地区天然径流量等数据系列，作降水径流双累计曲线，对降水径流多年累计量关系进行分析。天然径流量为实测径流量与用水量之和，用水量为柳河地区地表水净消耗量，经实际调查和分析统计得到具体数据。采用线性相关法，利用一元回归方程作累计降水量和累计实测径流量关系趋势曲线。点绘累计降水量和累计实测径流量，可以看出数据点有明显的变化，初步可判断整个系列不是同一系统，需要确定曲线转折点，进行时段划分。首先选取变化点前后两部分点据作不同的系列，分别作系列的一元回归趋势线，前后2条趋势线交叉点为曲线转折点，同时得到1个相关参数值；其次对选取点据进行增减重复作上步工作，对得到的相关参数值进行比较，当该值达到最大时，即可确定曲线转折点，该点即为时段划分的结束或开始点据，查看此点的年份就得到了时段划分的起始年份。柳河地区累计降雨量与累计径流量双累计曲线，如图3所示。

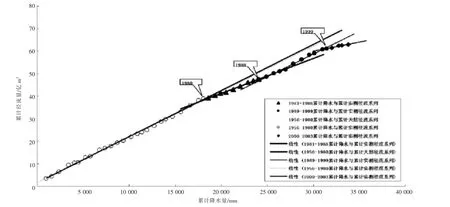
图3 柳河李营站累计降水量—累计实测径流量关系

从图3中可以看出，双累计曲线的转折点分别为1980、1988、1999年，由此可以获得4个时段系列，分别为 1956—1980、1981—1988、1989—1999、2000—2003年4个不同变化时间段。

1956—1980年时段，社会经济不发达，人类活动影响较小，流域下垫面变化较小，用水量是影响入库实测径流量的主要因素，计算后的入库天然径流量能反映实际径流量，降水与径流关系接近天然状态，因此以1980年以前的累计降水和累计天然径流量关系作为分析对比不同时段入库径流量减少的依据。另外3个时段累计曲线呈明显偏离趋势，1981年开始曲线突变，1981—1988年时段变化趋势极为明显，1989年以后变化趋势趋于平缓，1989—1999年时段走向接近1956—1980年时段的曲线趋势，2000年以后曲线又发生了急剧变化，体现了除用水量外不同时段其他因素的变化造成了入库流量的变化，显示了降水径流关系不同时段发生了某种改变，为进一步分析降水径流之间的关系提供了时段划分依据。

3.3.2 年降水径流相关关系分析

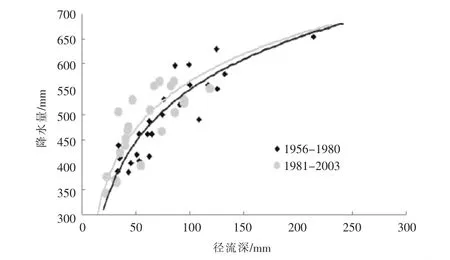
图4 柳河地区年降水径流相关关系

经降水径流双累计曲线的分析，得到了柳河入库水量变化的总量，确定了用水量因素影响的入库减少量。因此，对其他影响因素造成的减少量需进一步研究，分析降水径流关系来明确其他影响因素的包括范围和影响程度，得到不同因素影响造成的入库减少量。

选用1956—2003年的柳河流域内实测降水量资料和天然径流量资料计算径流深，用相关法分析降水径流关系，可得柳河地区年降水量与径流深关系曲线，如图4所示。从图4中可以明显看出，尽管降水径流关系较为散乱，但仍然呈现出了系统性的差异，20世纪80年代以后降雨径流关系曲线左移，同样的降水所产生的径流明显减少，其间的差异代表了下垫面条件变化影响。