基于声矢量传感器阵的汽车加速噪声源方位辨识

单泽涛, 单泽彪,, 梁龙凯, 石要武

(1. 保定市诺博橡胶制品有限公司, 河北 保定 071000； 2. 吉林大学 通信工程学院, 长春 130022；3. 中水东北勘测设计研究有限责任公司, 长春 130021)

0 引 言

汽车噪声源方位辨识研究对汽车工业的发展有着极其重要意义。汽车噪声不仅是一种环境污染而且也是影响汽车整体性能指标的一个重要因素。汽车噪声源方位辨识是控制和降低汽车噪声、 提高汽车产品品质的基本手段, 也是判段汽车故障类型的主要方法。噪声源辨识问题一直是国内外众多科研工作者们竞相研究的热点[1-5]。目前, 对汽车噪声源识别主要有两大类： 1) 基于试验的传统噪声源识别方法, 如, 铅覆盖法、 表面振速法、 声强法以及声全息法等, 这类识别方法对测试环境的要求和试验成本都较高, 而且辨识试验周期较长, 一般难以获得普遍应用； 2) 基于现代信号处理技术的噪声源识别方法, 主要有谱分析技术、 时频分析方法以及盲分离技术等。与传统的噪声源识别方法相比, 该识别方法试验过程简单, 对试验环境和设备要求较低, 但这类方法中对噪声源方位辨识大多应用标量声压传感器, 标量传感器在测量信号时, 测得的数据只有声压信息, 而在信号处理过程中还需要声速等信息； 另外, 传统的声压传感器信号处理方法大多是建立在一个声全息面上的分析和计算, 而声全息理论需要在无限大平面上进行测量, 实际工程中无法满足, 这就造成该方法在实际应用中仅是一种数学上的近似。因此, 无论在全息面上采用什么方法都是在近似的数学基础上进行分析, 得到的结果误差较大。

针对这些问题, 梁龙凯等[6]在均匀等间距直线阵排列时, 采用一种新型传感器----声矢量传感器(AVS: Acoustic Vector Sensor)[7-11]对汽车噪声源进行了方位参数估计研究, 取得了一定的成果, 但在信噪比较低时估计效果并不理想, 容易产生错误的噪声源点。故笔者采用了均匀分布面阵排列的声矢量传感器阵对噪声源进行方位辨识, 获得了更好的估计效果, 在信噪比为0时仍能准确估计噪声源的方位信息。声矢量传感器可同步、 共点、 直接测量声场空间中一点处的声压标量和质点振速矢量, 相对于标量声压传感器阵(PSA: Pressure Sensor Array), 利用矢量传感器阵能获得更为优越的目标定位性能[12,13]。声矢量传感器在测量时所采集的信息非常丰富并且具有指向性, 因此, 可摆脱全息理论的束缚, 并且采用其测量得到的准确数据对噪声源进行参数估计, 可提高参数估计的分辨率, 减小方位估计误差。

汽车加速过程中的噪声是一种复杂的多成分噪声, 在已有的研究中发现汽车的燃烧噪声为其主要噪声且在一个特定转速范围内是一个线性调频信号[14], 尤其是在3 600～4 400 r/min的转速下更呈现出线性调频特性, 因此, 把其简单归结为一个线性调频Chirp信号, 予以分析。针对Chirp信号的时频特性, 研究了声矢量传感器并采用多重信号分类(MUSIC: Multiple Signal Classification)算法对目标进行方位辨识问题。在等间距直线阵排列情形下, 基于声矢量传感器阵对双目标噪声源进行了方位估计, 并将计算结果与传统声压阵结果进行了比较。研究了声矢量传感器在等间距直线阵和均匀分布面阵两种排列情形下对单目标噪声源的方位估计。从以上两种情形结果对比分析可知, 采用均匀分布面阵的声矢量传感器更能有效地估计出噪声信号的方位参数, 从而获得噪声源的具体方位信息, 进而为汽车噪声的控制提供有力的科学依据。

1 声矢量传感器阵列输出模型

实际中, 汽车加速过程中的噪声检测装置到汽车噪声源的距离远大于其自身的孔径, 则可认为其入射波为平面波。因此, 设K个窄带平面波噪声源信号入射到由M个声矢量传感器构成的阵列上, 传感器在空间的位置矢量为km,m=1,2,…,M, 则在t时刻第m个声矢量传感器的阵列输出可表示为

(1)

其中uk=[1,cosθksinφk,sinθksinφk,cosφk]T,nmv(t)=[nmp(t),nmvx(t),nmvy(t),nmvz(t)]T是一个四维列向量, 表示第m个传感器声压和阵速同道接收到的噪声,sk(t)是第k个入射噪声源信号,am(Θk)是第m个传感器对信号sk(t)的响应系数,Θk=(φk,θk)为第k个信号的二维空间到达角。

将式(1)表示为矩阵形式, 并用符号Z(t)表示, 则传感器阵列输出为

Z(t)=[z1(t),z2(t),…,zM(t)]T=[a(Θ1)⊗u1,a(Θ2)⊗u2,…,a(Θk)⊗uk]S(t)+Nv(t)

(2)

其中符号⊗表示直积,S(t)称为噪声源矢量或入射波前矢量,Nv(t)为阵列接收到的噪声矢量。令Av(Θ)=[a(Θ1)⊗u1,a(Θ2)⊗u2,…,a(Θk)⊗uk], 称其为声矢量阵的信号方向矩阵, 则式(2)可写成

Z(t)=Av(Θ)S(t)+Nv(t)

(3)

由Av(Θ)的定义可知, 声矢量阵的方向矢量是声压阵的方向矢量与一个只与声波传播方向有关的列向量的直积, 用av(Θ)表示声矢量阵的方向矢量, 则其可表示为

av(Θ)=a(Θ)⊗u(Θ)

(4)

其中u(Θ)=[1,cosθsinφ,sinθsinφ,cosφ]T。

根据声矢量传感器阵元在空间排列形式的不同, 将得到不同的方向矢量, 下面分析两种常用阵列： 均匀等间距直线阵和均匀分布面阵, 其几何结构分别如图1和图2所示。

图1 均匀等间距直线阵 图2 均匀分布面阵

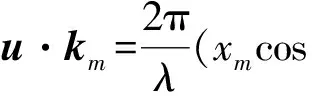
av(Θ)=[e-ju·k1,e-ju·k2,…,e-ju·kM]T⊗u(Θ)

(5)

声矢量传感器分布为均匀等间距直线阵列时的几何结构如图1所示, 相邻阵元间距为d, 则第m个阵元的位置坐标即为(0,md,0), 带入式(5)可得到均匀等间距直线阵的方向矢量为

av(Θ)=[1,e-jβ,…,e-j(M-1)β]T⊗u(Θ)

(6)

声矢量传感器分布为均匀分布面阵列时的几何结构如图2所示, 若相邻阵元间距为d, 则第n行第m列阵元的位置坐标即为(nd,md,0), 带入式(5)可得到均匀分布面阵的方向矢量为

av(Θ)=[1,e-jξ(cos θ+sin θ),…,e-jξ[(N-1)cos θ+(M-1)sin θ]]T⊗u(Θ)

(7)

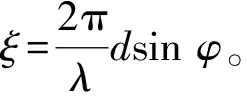
2 汽车噪声源方位辨识

设声矢量传感器阵接收到的噪声源信号与其他噪声不相关, 声矢量传感器阵列输出模型如式(3)所示, 用Rv表示其协方差矩阵, 则有

(8)

其中Iv=diag[1,1/3,1/3,1/3,…1,1/3,1/3,1/3]是声矢量阵的噪声归一化协方差矩阵。对Rv进行特征分解, 并将其特征向量依据特征值的降序排列可得到

(9)

其中Rv中有K个较大的特征值对应于噪声源信号项, 4M-K个较小的特征值对应其他噪声项, 于是得到一个由K个特征向量构成的信号子空间和由4M-K个特征向量构成的噪声子空间, 并且这两个子空间正交。由信号的方向矢量av(Θ)所张成的空间与特征向量Uvs所张成的空间是同一个空间得知,av(Θ)与噪声子空间Uvs也正交, 利用此正交性便可得到声矢量传感器阵的MUSIC空间谱

(10)

通过式(10)进行谱峰值搜索, 即可得到噪声源信号方位估计。

3 仿真实验

图3 基于声压传感器阵的信号方位估计

实验1 首先验证声矢量传感器阵列对两个噪声源目标的分辨能力。假设空间有两个Chirp信号, 起始截止频率分别取0.05 kHz,0.3 kHz和0,0.5 kHz, 入射方向为θ1=30°,φ1=45°和θ2=31°,φ2=46°, 信噪比取20 dB。声矢量传感器阵以d=λ/2等间距均匀分布于直线阵x轴上, 其中λ为声波波长, 阵元个数M=8。为进行对比, 同时给出了传统声压阵MUSIC方位估计结果, 仿真结果如图3及图4所示。

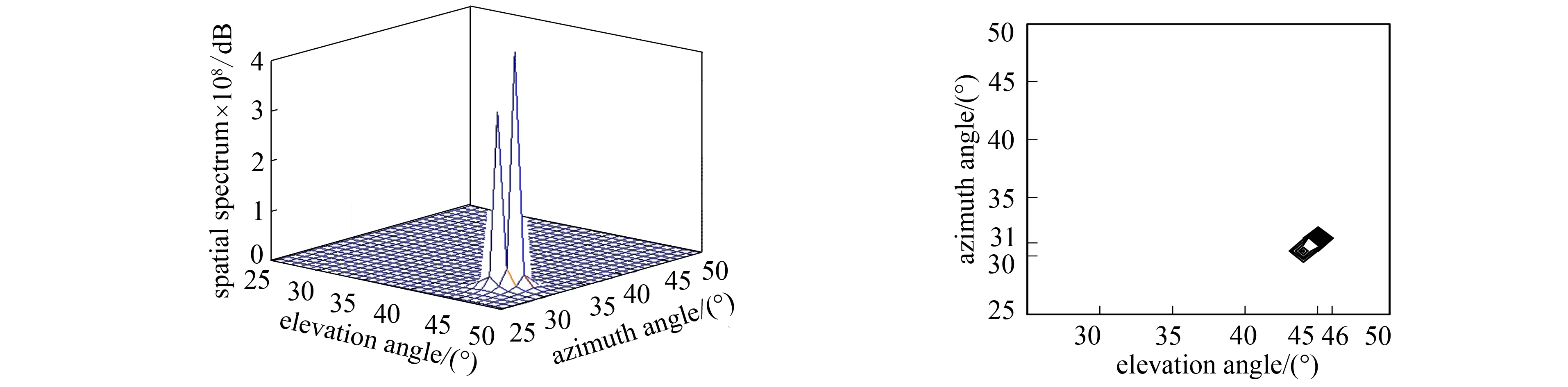
a 三维图 b 等高线图

图3是基于传统声压阵的MUSIC算法对双目标进行方位估计的结果。当传感器阵列为均匀线阵排列时, 传统声压阵不能对其进行二维估计。从图3可看出, 当空间两个Chirp信号的方位角(或俯仰角)相差1°时, 传统声压阵不能对其进行有效分辨。

图4是基于声矢量传感器阵的MUSIC算法对双目标的方位估计结果。从图4可看出, 声矢量传感器阵为均匀线阵排列时可对目标进行二维方位参数估计, 这也验证了声矢量传感器在获得质点振速信息后具有指向性这一特性。从图4可看出, 即使目标的方位角和俯仰角均相差1°, 声矢量传感器阵列仍能对信号进行准确的方位估计, 这说明声矢量传感器阵在获得更丰富的信息后大大提高了分辨率。

实验2 对矢量阵在按照均匀等间距直线阵和均匀分布面阵排列时对单目标噪声源的分辨能力进行仿真。假设噪声源Chirp信号以方向θ1=30°,φ1=45°分别入射到均匀等间距直线阵和均匀分布面阵上, 其信噪比分别取5 dB和0, Chirp信号起始截止频率分别为0.05 kHz和0.3 kHz, 阵元个数均取M=9, 相邻阵元间距均为d=λ/2。方位估计结果分别如图5及图6所示。

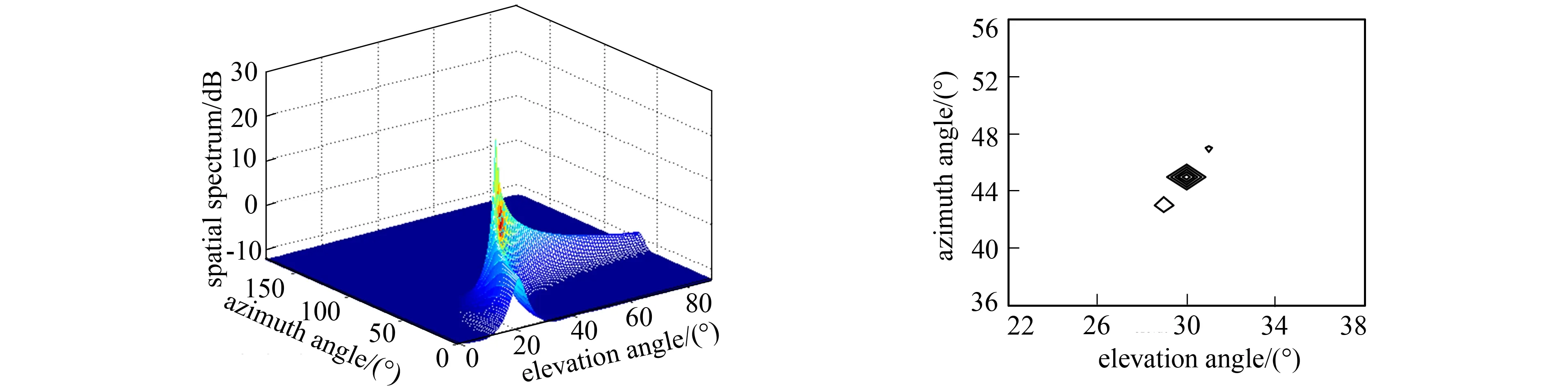
a 三维图 b 等高线图

从图5可看出, 在信噪比为5 dB时, 采用等间距直线阵排列的声矢量传感器的MUSIC算法对噪声源方位估计的效果并不是很理想, 估计方位比较模糊。从图5b可看出, 有额外两个误差噪声源的存在, 且随着信噪比的下降或在周围噪声更复杂的条件下, 估计效果变得更差。

a 三维图 b 等高线图

图6是信噪比为0时以均匀分布面阵排列的声矢量传感器的噪声源信号方位估计。从图6可看出, 在采用面阵排列时的声矢量传感器能更准确地估计出噪声源方位参数信息, 与前面采用线阵方式相比, 估计精度略有下降, 但此时信噪比为0。所以, 采用均匀面阵排列的声矢量传感器可更有效地进行噪声源方位估计, 可有效提高信噪比和分辨率, 增强抗干扰能力, 同时还减小了方位估计误差。

4 结 语

笔者讨论了基于声矢量传感器阵的汽车加速噪声源方位辨识问题。把汽车加速过程中的主要噪声----燃烧噪声在一定的转速范围内归结为一个线性调频Chirp信号, 然后利用声矢量传感器能获得声压和振速的双重特性对汽车加速过程中的噪声进行数据采集, 再利用MUSIC经典算法分别对单目标和双目标进行分析处理, 最后估计噪声信号的方位参数, 获得了噪声源的具体方位信息。声矢量传感器的引入和均匀面阵的排阵方式, 提高了汽车噪声源方位辨识的分辨率, 减少了噪声对信号方位估计的影响, 从而更加贴近对汽车噪声源方位估计时的实际情况。该处理方法更具有工程实际意义, 同时也是对声矢量传感器在汽车噪声控制领域应用的尝试。

参考文献：

[1]赵彤航, 卢炳武, 曹蕴涛. 混合动力桥车振动噪声控制技术 [J]. 吉林大学学报： 工学版, 2012, 42(6)： 1373-1377.

ZHAO Tong-hang, LU Bing-wu, CAO Yun-tao. NVH Control Technology of Hybrid Electric Vehicle [J]. Journal of Jilin University: Engineering and Technology Edition, 2012, 42(6)： 1373-1377.

[2]司春棣, 陈恩利, 杨绍普, 等. 汽车噪声源识别实验研究 [J]. 噪声与振动控制, 2010, 1(2)： 40-43.

SI Chun-di, CHEN En-li, YANG Shao-pu, et al. Experimental Study on Noise Sources Identification of Vehicle [J]. Noise and Vibration Control, 2010, 1(2)： 40-43.

[3]李兵, 杨殿阁, 邵林, 等. 基于波束形成和双目视觉的行驶汽车噪声源识别 [J]. 汽车工程, 2008, 30(10)： 889-892.

LI Bing, YANG Dian-ge, SHAO Lin, et al. Noise Sources Measurement and Identification for Moving Automobiles [J]. Automotive Engineering, 2008, 30(10)： 889-892.

[4]陈书明, 王登峰, 陈鑫. 小波变换在轿车车内噪声源识别中的应用研究 [J]. 噪声与振动控制, 2009, 2(4)： 88-92.

CHEN Shu-ming, WANG Deng-feng, CHEN Xin. Study on Application of Identification of Interior Noise Source in Cars with Wavelet Transform [J]. Noise and Vibration Control, 2009, 2(4)： 88-92.

[5]邓江华, 顾灿松, 刘献栋, 等. 基于声阵列技术的汽车噪声源识别及贡献量分析 [J]. 振动控制学报, 2010, 23(6)： 630-635.

DENG Jiang-hua, GU Can-song, LIU Xian-dong, et al. Sound Source Indentification and Contribution Based on Acoustic Array Technology [J]. Journal of Vibration Engineering, 2010, 23(6)： 630-635.

[6]梁龙凯. 基于声矢量传感器的汽车加速噪声方位参数估计方法研究 [D]. 长春： 吉林大学通信工程学院, 2011.

LIANG Long-kai. Research on Methods for Car Accelerating Noise Position Parameter Estimation Based on Sound Vector Sensor [D]. Changchun: College of Communication Engineering, Jilin University, 2011.

[7]孙贵青, 李启虎. 声矢量传感器信号处理 [J]. 声学学报, 2004, 29(6)： 491-498.

SUN Gui-qing, LI Qi-hu. Acoustic Vector Sensor Signal Processing [J]. Acta Acustica, 2004, 29(6)： 491-498.

[8]CHEN H W, ZHAO J W. Wideband MVDR Beam Forming for Acoustic Vector Sensor Linear Array [J]. IEEE Proc Radar Sonar Navig, 2004, 151(3): 158-162.

[9]CHEN H W, ZHAO J W. Coherent Signal Subspace Processing of Acoustic Vector Sensor Array for DOA Estimation of Wideband Sources [J]. Signal Processing, 2005, 85(1): 837-847.

[10]NAN ZOU, CHIA CHIN SWEE, CHEW B A L. Vector Hydrophone Array Development and Its Associated DOA Estimation Algorithms [C]∥OCEANS 2006 Asia Pacific. Singapore: [s.n.], 2006: 1-5.

[11]ABDI A, GUO Huai-hai. Signal Correlation Modeling in Acoustic Vector Sensor Arrays [J]. IEEE Trans Signal Processing, 2009, 57(3): 892-903.

[12]WONG K T, ZOLTOWSKI M D. Self-Initiating MUSIC-Based Direction Finding in Underwater Acoustic Particle Velocity-Field Beam Space [J]. IEEE J Oceanic Eng, 2000, 25(2): 262-273.

[13]WONG K T, ZOLTOWSKI M D. Root-MUSIC-Based Azimuth Elevation Angle-of-Arrival Estimation with Uniformly Spaced but Arbitrarily Oriented Velocity Hydrophones [J]. IEEE Trans Signal Processing, 1999, 47(12): 3250-3260.

[14]徐红梅. 内燃机振声信号时频特性分析及源信号盲分离技术研究 [D]. 杭州： 浙江大学机械与能源工程学院, 2008.

XU Hong-mei. Time-Frequency Analysis of Engine Vibration and Noise Signals and Research on the Blind Separation Technology for Source Signals [D]. Hangzhou: College of Mechanical and Energy Engineering, Zhejiang University, 2008.