轴承位置对涡轮泵转子系统稳定性的影响研究

窦 唯，褚宝鑫

（北京航天动力研究所，北京 100076）

0 引言

低温液体火箭发动机涡轮泵转子通常在高转速下工作，转子的振动特性直接影响火箭发动机的性能。轴承为旋转轴系提供刚度，其轴向位置对转子系统动态特性有着重要的影响，包括转子系统的临界转速、振型、不平衡响应以及稳定性特性等[1-15]。因此，开展轴承轴向位置对涡轮泵转子系统稳定性的影响研究具有重大的理论和工程实际意义。

本文针对低温液体火箭发动机涡轮泵转子非线性系统开展了轴承轴向位置对动力稳定性的影响研究。建立了涡轮泵转子系统的非线性动力学模型，分别研究了理想安装情况下和非理想安装情况下泵端和涡轮端轴承轴向位置变化对转子系统稳定性的影响，给出了失稳转速随轴向位置的变化规律，为液体火箭发动机涡轮泵转子系统结构设计、故障诊断与安装维护提供理论依据。

1 液体火箭发动机涡轮泵转子系统数学模型

涡轮泵转子轴系主要包括转子、轮盘、轴承和密封等，本文采用有限元方法形成涡轮泵转子轴系的刚度、质量和陀螺矩阵；进而建立涡轮泵转子系统的动力学模型。

1.1 非线性密封力模型

涡轮泵转子系统在实际运行时，其密封结构不仅起到减弱流体逸出的作用，同时近似为滑动轴承结构，滑动轴承的交叉刚度项可引起轴系的失稳。本研究在计算时，将密封结构做滑动轴承处理，并采用Capone非线性密封力模型。该模型由Capone于1986年推导得出，是基于短圆柱瓦轴承假设得到的[5-6]，即忽略了密封压力沿周向变化产生的影响。

径向滑动轴承的几何关系如下图1所示。

轴承长度即垂直于纸面方向为z轴；c为轴承的半径间隙；图中O为轴承的几何中心，OJ为轴颈的几何中心，R为轴颈半径；W为轴颈所承受的载荷；Ω为转子的转速；e为偏心距；θ为转角；φ为偏位角。

由于Capone非线性密封力模型是基于短轴承理论假设提出的，因此可以忽略Reynold方程中压力梯度沿周向的变化，即可得到流体密封中的压力的微分方程的无量纲形式，可以简写为下式

可以获得无量纲流体密封压力表达式为

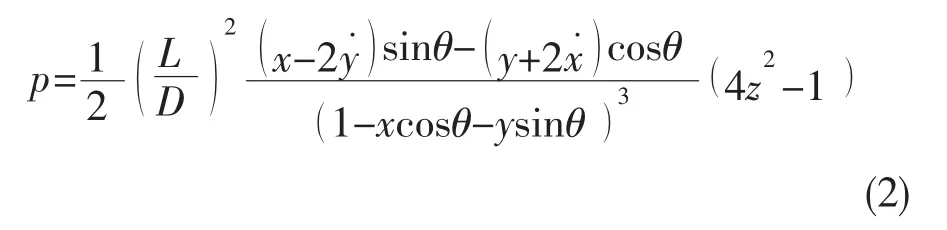
如图1所示，当转角θ在区间[β，β+π]内时，流体密封所形成的压力区域为正压区，其中，角度β的值可由下式得到

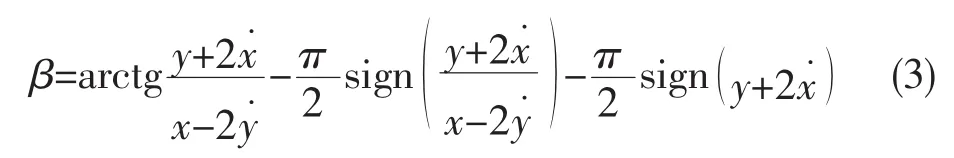
由自由边界条件可知，流体密封在空穴区和轴承两端的压力为零，故在轴承边界上流体密封压力为0。

对式 (2)沿着轴颈表面密封流体作用的弧段积分，就可得到非线性流体密封力的无量纲表达式如式 (4)所示

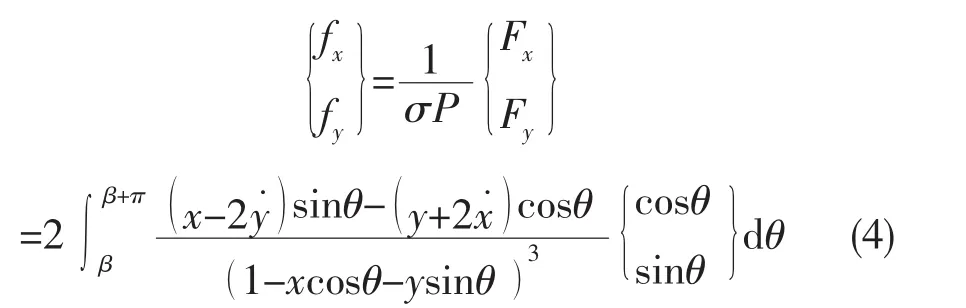
对上式积分，就可得到无量纲非线性密封力fx和fy的最后的表达式

将根据短圆柱瓦轴承理论得到的无量纲的Capone非线性密封力fx和fy转换成有量纲的非线性密封力Fx和Fy，得到的表达式如式(9)所示

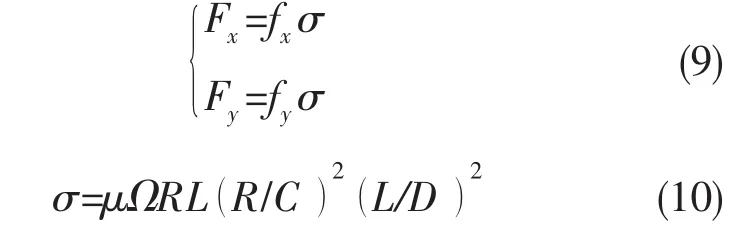
式中：σ为轴承特性参数；μ为轴承密封流体粘度；Ω为转子转速；R为轴颈半径；L为轴承有效长度；D为轴承直径。

1.2 转子系统数学模型

将涡轮泵转子划分为若干个轴段，每个轴段单元采用Timoshenko梁单元模型，这样就可建立涡轮泵转子系统的无阻尼自由运动微分方程。

弹性轴的无阻尼自由运动微分方程如式 (11)所示

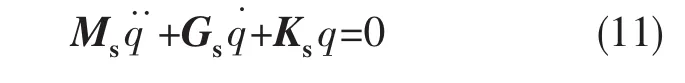
式中：q为弹性轴节点的位移向量；Ms为弹性轴的一致 (协调)质量矩阵；Ks为弹性轴的刚度矩阵；Gs为弹性转轴的陀螺矩阵。

由动能定理及根据Lagrange方程可以得到轮盘的运动方程如式 (12)所示

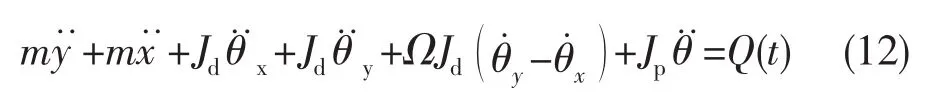
式中：Q(t)为作用在轮盘上的外力，N。

写成矩阵形式为

式中：Md为轮盘的质量矩阵；Gd为轮盘的陀螺矩阵。

由于制造加工及装配等误差的影响，实际运行的转子轮盘系统不可避免地会存在不平衡量，且轮盘部分的不平衡量远大于弹性轴段部分。本文在计算转子轴系的稳定性时只考虑轮盘结构(即涡轮、离心轮、诱导轮)的影响。

不平衡激励力的表达式为

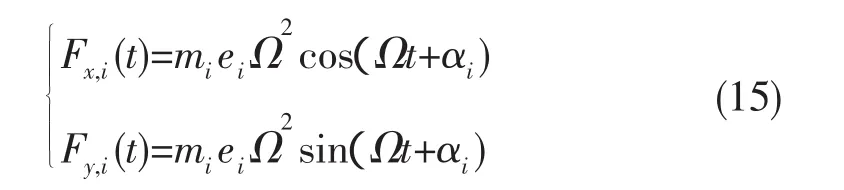
式中：mi为轮盘的质量；ei为该轮盘的偏心距；αi为该轮盘的初始偏位角。将不平衡力写为向量的形式为

式中：Fu,i即为轮盘不平衡量在转子节点i处所产生的不平衡激励力，表达式中各行对应转子节点i 处的四个自由度

然后根据涡轮泵轴系的轴承所在节点及作用在轴承上的载荷，从而可计算四个轴承刚度系数和四个支承结构的阻尼系数（不考虑游隙的影响）。

若轴颈中心的坐标为xs和ys，则轴承作用于涡轮机节点处的轴承力和分别为

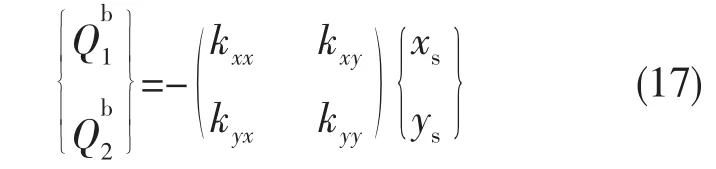
将线性轴承力移到系统的运动微分方程的左端，对轴承所在的节点而言，系统的运动微分方程中与节点的振动有关的项可以写成下式

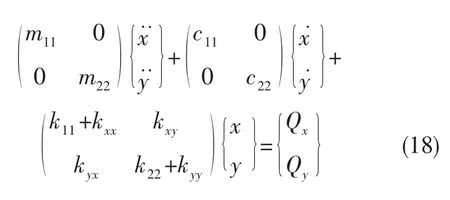
因此，可以把每个轴承的刚度系数分别根据轴承所在的节点位置加到弹性轴的刚度矩阵上Ksi(i=1,2)，得到考虑了轴承刚度的转子－轴承系统的刚度矩阵Ksbi(i=1,2)。

把轮盘的质量矩阵Md按照轮盘所在的节点对应的自由度加到弹性转轴的一致质量矩阵Ms对应的位置上，形成转子－轮盘系统的质量矩阵。同理，把轮盘的陀螺矩阵Gd按照轮盘所在位置加到转子的陀螺矩阵Gs上，形成转子－轮盘系统的陀螺矩阵。

按照节点的排列顺序将转子－轮盘系统的质量、刚度和陀螺矩阵组合成系统的整体质量矩阵M，整体刚度矩阵K和整体陀螺矩阵G。

根据系统的刚度矩阵、陀螺矩阵和质量矩阵，可得到转子－轮盘－轴承系统的无阻尼自由振动微分方程为

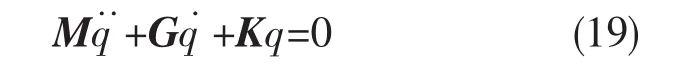
考虑不平衡激励力、密封非线性液膜力及转子-轴承系统的阻尼作用时，可得到转子－轮盘－轴承系统的有阻尼强迫振动微分方程为

1.3 涡轮泵转子模型简化

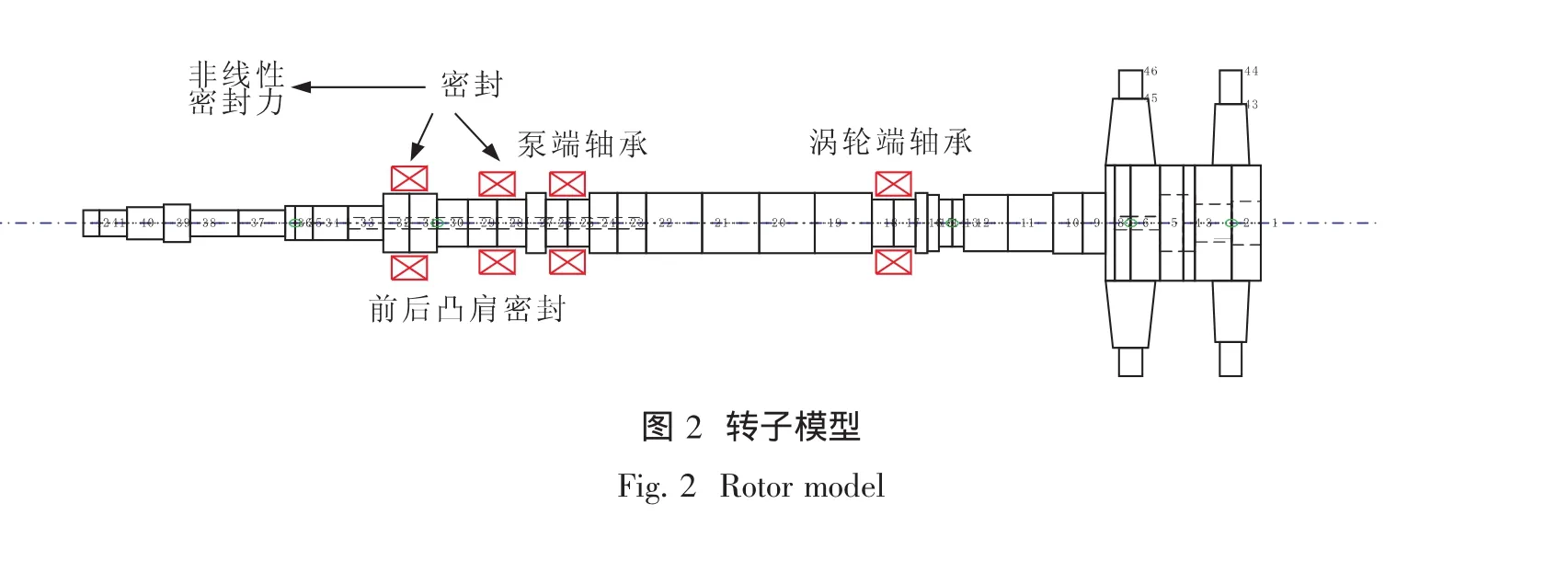
涡轮泵转子系统主要由转子、离心轮和诱导轮三部分组成。工作时，三部分结构一起旋转。建立有限元模型时，须对各部分连接区域进行适当简化。该转子系统主要通过两个滚动轴承支承，其中密封结构也能起到一定的支承刚度作用，在稳定性分析中均将其作滑动轴承近似处理。文中所提支承刚度均指轴承、鼠笼及阻尼器的总刚度。综上，涡轮泵转子系统的有限元模型如图2所示，轴系总长420 mm，共划分为41个梁单元及4个轮盘单元，由两个滚动轴承及两个迷宫密封结构共同支承。

模型主要进行以下简化：将涡轮转子的轴套结构等效为转子的一部分；轮盘、诱导轮和离心轮简化为规则结构，并附加部分集中质量和转动惯量；动环结构以集中质量、集中转动惯量近似处理。

2 液体火箭发动机涡轮泵转子系统非线性稳定性分析

轴系稳定性分析主要计算轴系由于低频涡动产生液膜振荡的频率大小及低频振荡出现时的转速，即失稳转速。因为流体密封力是非线性因素，并且系统的动力学模型是高维方程，本文采用直接积分法来求解系统的动态响应。因为Newmark方法的2个参数满足一定值时，该方法是无条件稳定的，所以本文采用Newmark方法逐步积分，计算一系列不同转速下转子的动力学响应，确定转子的低频成分，其中转速间隔取为200 r/min。数值仿真无量纲时间步长取π/500，Newmark方法的收敛偏差标准取2×10-6。仿真500个周期，舍弃非稳态数据，取后50个周期稳态数据进行分析。

轴系的稳定性计算采用梁单元模型编程实现，计算时简化了转子结构，去掉轮盘结构，将轮盘的质量、转动惯量附加到相应质心处；另一方面，稳定性计算时密封结构采用上文的非线性流体密封力模型。

理想情况下，轴系在安装时各轴段轴线及密封、轴承的中心轴线等完全重合。实际工作中，轴系安装时总会存在偏心，此时密封结构的液膜厚度会发生变化，并影响转子的动力特性。为此，分析中引入安装偏心影响因素。考虑到安装偏心小于密封间隙，因此给定为10 μm。

2.1 无安装偏心时泵端轴承位置变化时稳定性分析

将轴承在模型原始位置处轴向调整±5 mm，计算轴承位置对轴系稳定性的影响，由图2可知，离心轮和涡轮分别支承轴承的外侧，其中泵端轴承轴向位置为负值表示靠近离心轮，涡轮端轴承轴向位置为负值表示远离涡轮轮盘。分别取泵端轴承轴向位置为-5 mm，0 mm，5 mm三个值，计算不同泵端轴承轴向位置时失稳转速变化规律，不同泵端轴承轴向位置下失稳转速结果如表1所示，失稳转速随泵端轴承轴向位置的变化曲线见图3。

表1 泵端轴承位置对失稳转速影响Tab.1 Influence of position of bearing near pump on instability rotation speed

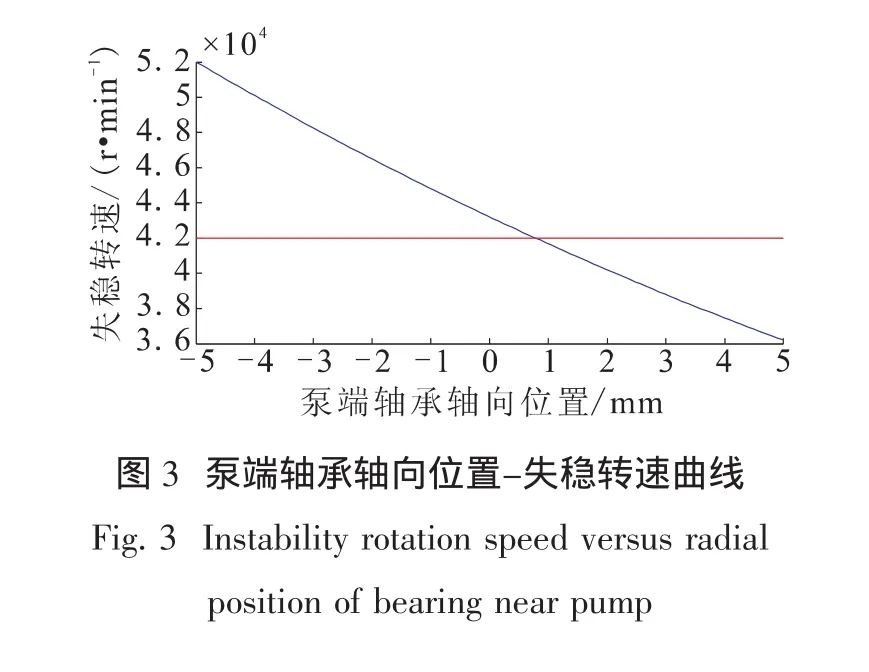
从表1中可以看出，当泵端轴承轴向位置在-5～5 mm范围内调整时，失稳转速变化明显，轴向位置为-5 mm时失稳转速值已经超出了计算范围，且随着泵端轴承远离密封结构轴系失稳转速减小，这是因为随着泵端轴承逐渐远离密封结构，在转子静挠曲及泵端轴承处转子静变形相对不变的条件下，转子在密封处静变形加大，密封激励力增大，密封非线性激励力越强，引发轴系不稳定因素增多，从而导致轴系更容易失稳。

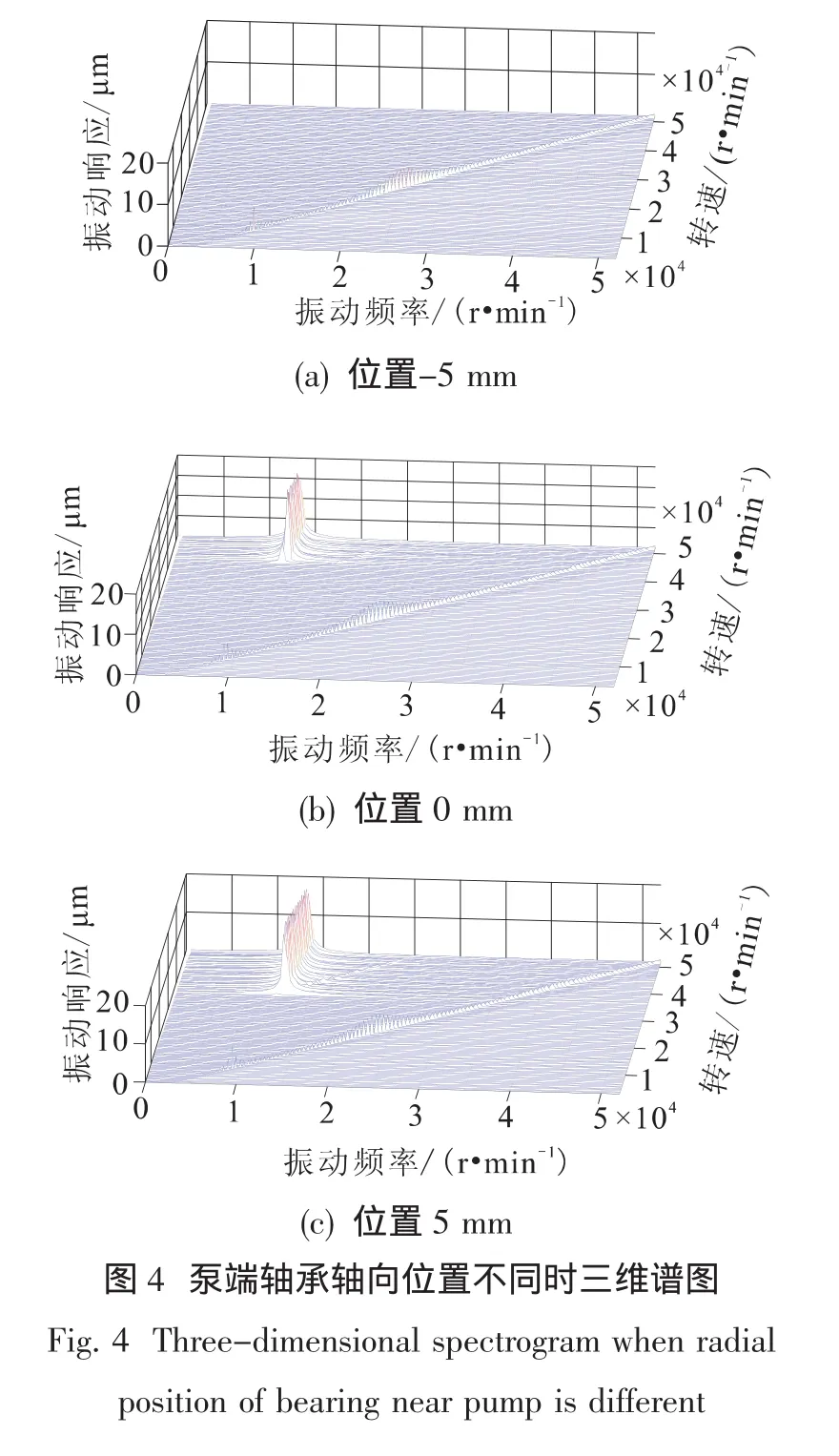
为了分析低频成分的变化规律，图4中给出了无安装偏心时不同泵端轴承轴向位置下离心轮后凸肩密封节点的三维谱图。

当安装偏心为0时，不同泵端轴承轴向位置下轴系也只有一阶涡动，且一阶涡动频率均在12 600 r/min附近。从三维谱图的基频曲线也可以看出，泵端轴承轴向位置在小幅度内变化时，轴系临界转速的变化也很小，一阶临界转速约为9 000 r/min，二阶临界转速约为24 000 r/min。

综上，泵端轴承轴向位置对轴系的失稳转速影响较大，但对一阶涡动的幅值及频率影响较小。随着泵端轴承逐渐远离密封结构，失稳转速逐渐减小；一阶涡动的频率约为12 600 r/min。

2.2 无安装偏心时涡轮端轴承位置变化时稳定性分析

分别取涡轮端轴承轴向位置为-5 mm，0 mm，5 mm三个值研究不同涡轮端轴承轴向位置时失稳转速变化规律，不同涡轮端轴承轴向位置下失稳转速结果见表2所示，失稳转速随涡轮端轴承轴向位置的变化曲线见图5。

表2 涡轮端轴承轴向位置对失稳转速影响Tab.2 Influence of radial position of bearing near turbine on instability rotation speed

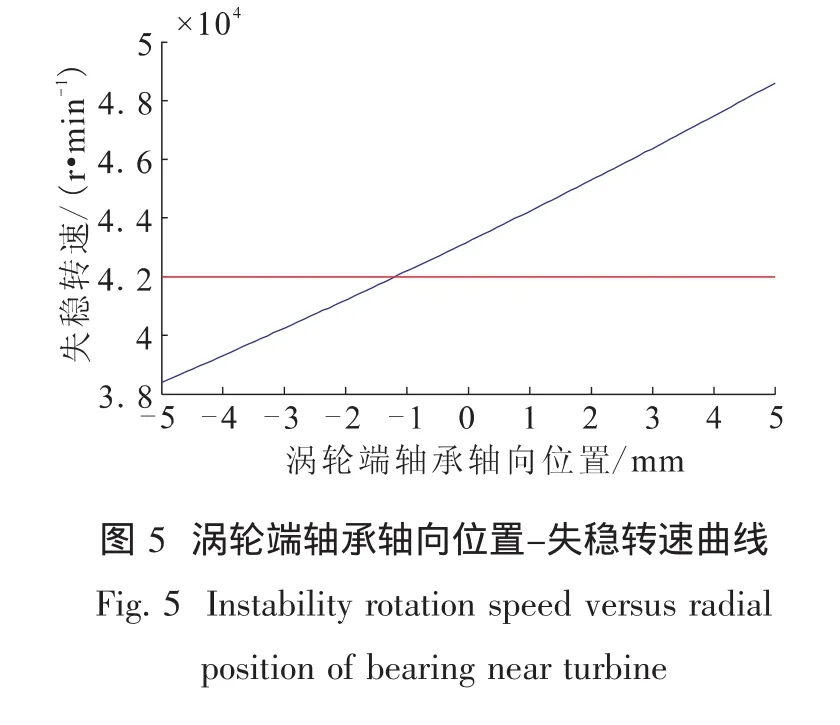
从表2中可以看出，涡轮端轴承轴向位置变化时，失稳转速也变化显著，但变化幅度小于泵端轴承轴向位置时的结果，且随着涡轮端轴承靠近涡轮轮盘，轴系失稳转速增大，这是因为随着涡轮端轴承逐渐远离密封结构 (即靠近涡轮轮盘)，相当于泵端轴承逐渐靠近密封，故稳定性结果与改变泵端轴承轴向位置时的结果相反。但由于该作用为间接的，因而没有直接改变泵端轴承轴向位置时效果显著。

为分析低频成分的变化规律，图6中给出无安装偏心时不同涡轮端轴承轴向位置下离心轮后凸肩密封节点的三维谱图。其中，涡轮端轴承轴向位置为0 m时的结果在图4（b）中已经给出，此处予以省略。

同样，当安装偏心为0时，不同涡轮端轴承轴向位置下轴系也只有一阶涡动，且一阶涡动频率均在12 600 r/min附近；虽然失稳转速变化显著，但一阶涡动的幅值几乎不随轴向位置的变化而变化。从三维谱图的基频曲线也可看出，涡轮端轴承轴向位置在小幅度内变化时，轴系临界转速的变化也很小，一阶临界转速约为9 000 r/min，二阶临界转速约为24 000 r/min。

综上，涡轮端轴承轴向位置对轴系的失稳转速影响仍较大，但小于泵端轴承轴向位置的影响效果，对一阶涡动的幅值及频率影响很小。随着涡轮端轴承逐渐靠近涡轮轮盘结构，失稳转速逐渐增大；一阶涡动的频率约为12 600 r/min。

2.3 有安装偏心时泵端轴承轴向位置变化时稳定性分析

与安装偏心等于0时的取值相同，计算安装偏心为10 μm时不同泵端轴承轴向位置下的失稳转速，其结果见表3。此时失稳转速随轴向位置的变化曲线见图7（与安装偏心等于0时的结果进行对比）。

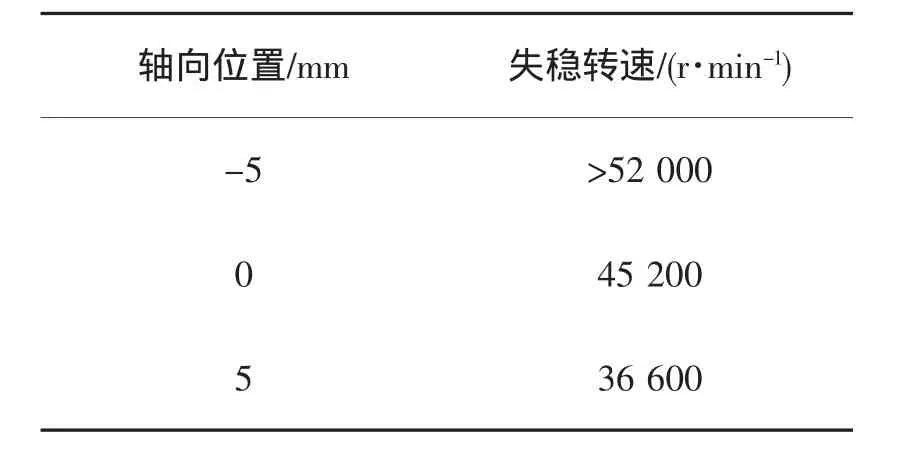
表3 泵端轴承轴向位置对失稳转速影响Tab.3 Influence of radial position of bearing near pump on instability rotation speed

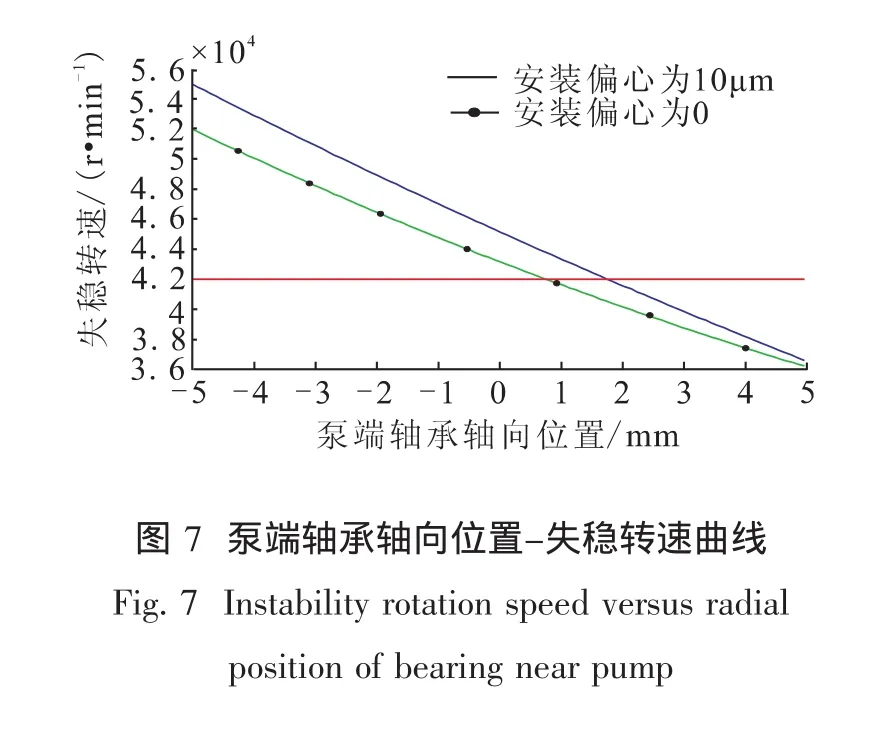
从图7中可以看出，增大安装偏心后，泵端轴承轴向位置对失稳转速的影响仍然较大，此时失稳转速变化规律与安装偏心为0时的结果基本相同，变化幅度略有增大，但数值较安装偏心为0时增大较大，轴向位置为-5 mm时失稳转速值也超出了计算范围。

为分析低频成分的变化规律图8中给出有安装偏心时不同泵端轴承轴向位置下离心轮后凸肩密封节点的三维谱图。

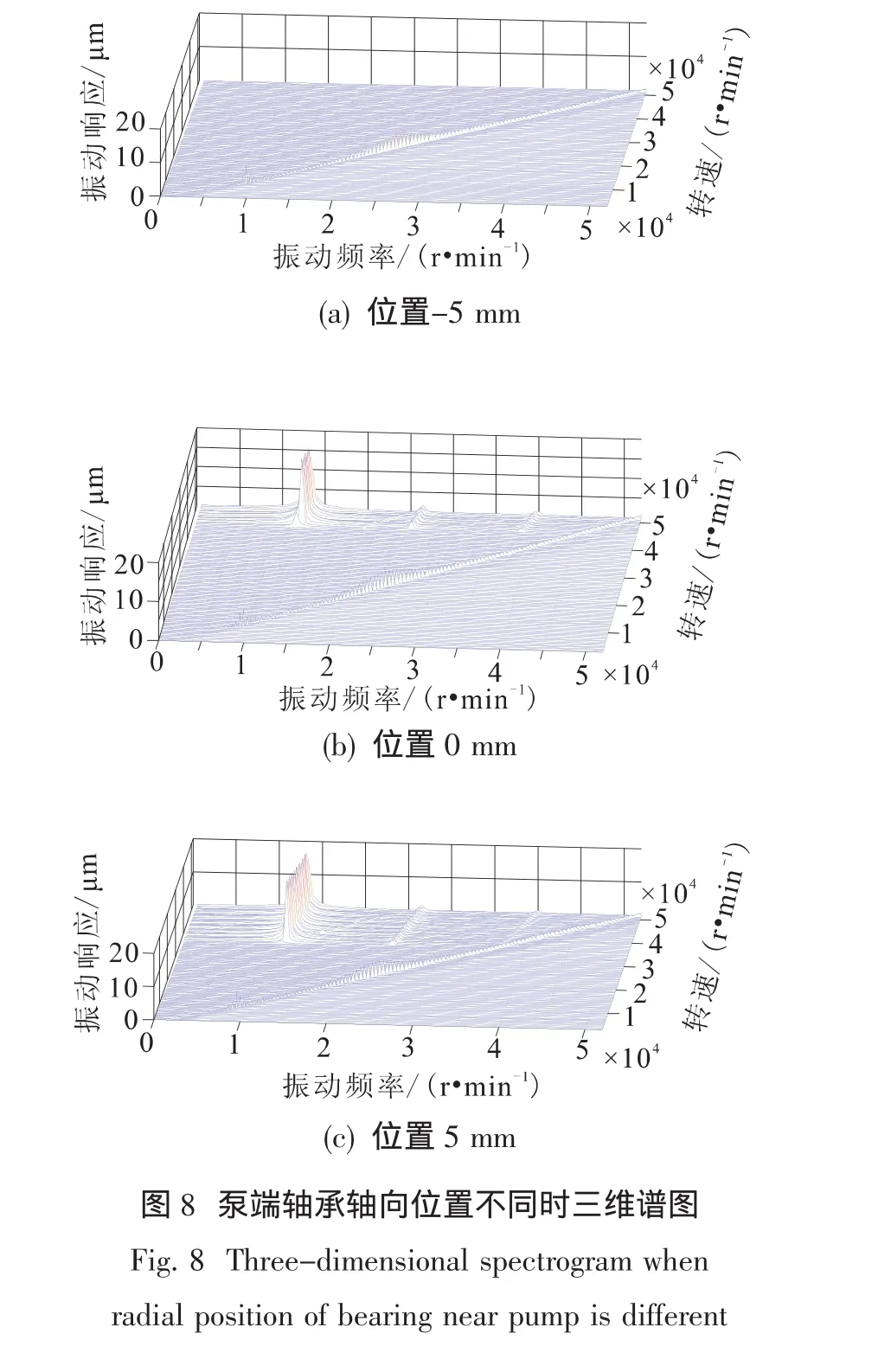
安装偏心增大后，轴系出现二阶、三阶涡动；随阶数增加，涡动幅值迅速降低，但各阶涡动幅值基本不随泵端轴承轴向位置的改变而改变；一阶、二阶涡动频率近似为12 600 r/min，24 000 r/min。

综上所述，增大安装偏心后，泵端轴承轴向位置对轴系的失稳转速影响仍然较大，但对各阶涡动的幅值及频率大小影响很小；同时，安装偏心增大会导致二阶、三阶涡动的出现。

2.4 有安装偏心时涡轮端轴承轴向位置变化时稳定性分析

与安装偏心等于0时的取值相同，计算安装偏心为10 μm时不同涡轮端轴承轴向位置下的失稳转速，其结果见表4。此时失稳转速随轴向位置的变化曲线见图9（与安装偏心等于0时的结果进行对比）。

表4 有安装偏心时涡轮端轴承位置对失稳转速影响Tab.4 Influence of position of bearing near turbine on instability rotation speed when installation eccentricity exists

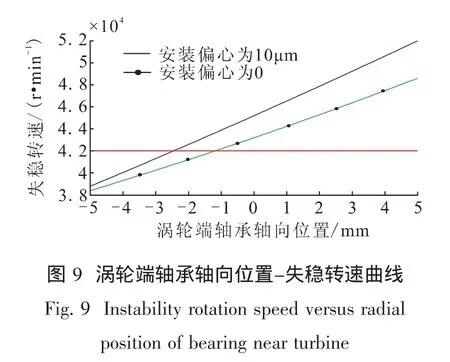
从图9中可以看出，增大安装偏心后，涡轮端轴承轴向位置对失稳转速的影响仍然较大，此时失稳转速变化规律与安装偏心为0时的结果基本相同，变化幅度略有增大，但数值较安装偏心为0时增大较大，同时轴向位置为5 mm时失稳转速值超出了计算范围。

为分析低频成分的变化规律，图10中给出了有安装偏心时不同涡轮端轴承轴向位置下离心轮后凸肩密封节点的三维谱图。其中，安装偏心10 μm，涡轮端轴承轴向位置为0时的结果在图8中已经给出，此处予以省略。

与泵端轴承轴向位置变化时的结果类似，安装偏心增大后，轴系开始出现二阶和三阶涡动；随着阶数增加，涡动幅值迅速降低，三阶涡动的幅值几乎为零，但各阶涡动幅值基本不随涡轮端轴承轴向位置的改变而改变；一阶、二阶涡动的频率近似为12 600 r/min和24 000 r/min。

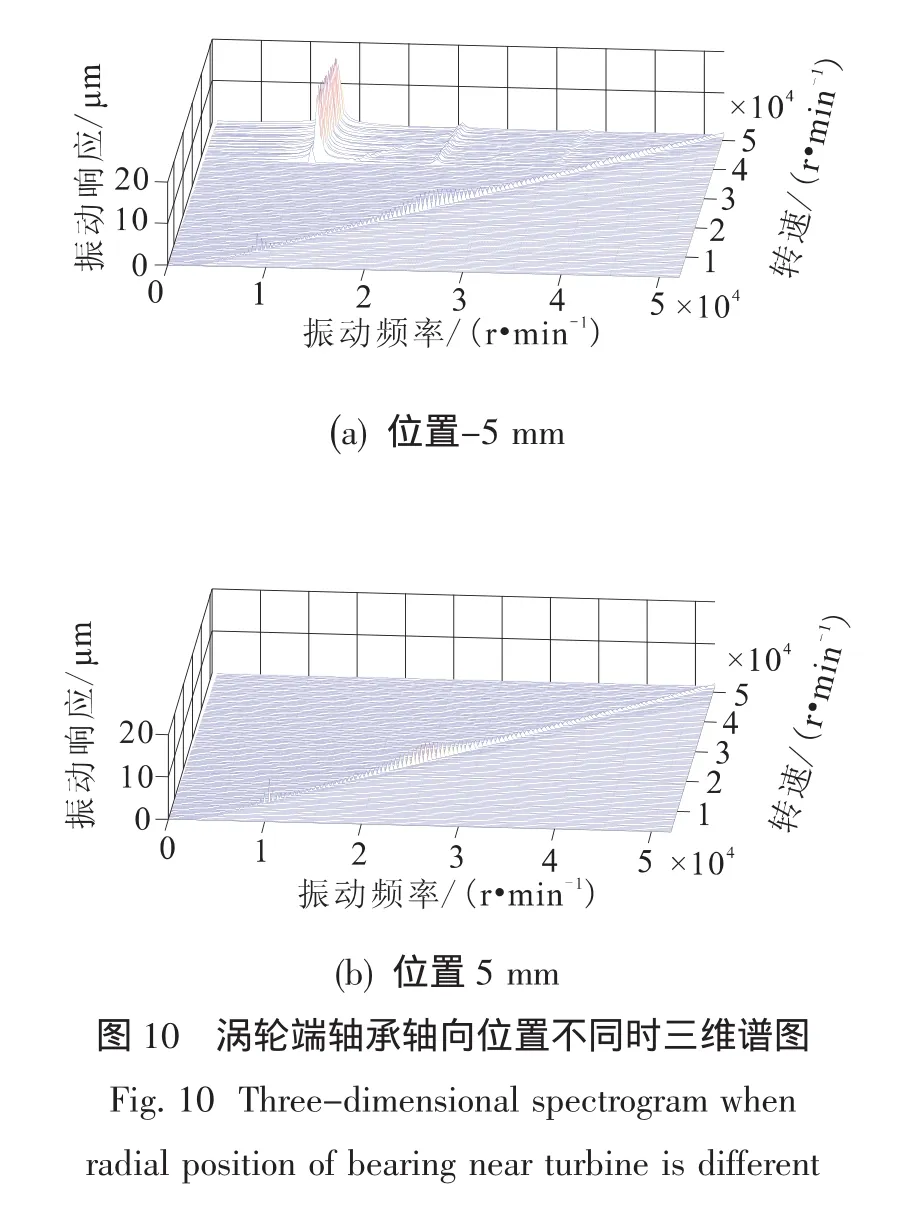
综上所述，增大安装偏心后，涡轮端轴承轴向位置对轴系的失稳转速影响仍然较大，但对各阶涡动的幅值及频率大小影响很小。

3 结论

通过研究轴承轴向位置对液体火箭发动机转子系统稳定性的影响研究，得出以下结论：

1)安装偏心为0时，不论轴承轴向位置如何变化，轴系均只存在一阶涡动；增大安装偏心后，轴系开始出现二阶、三阶涡动。

2)各阶涡动幅值和频率基本不受轴承轴向位置参数变化影响，随阶数增加，各阶涡动幅值迅速降低，一阶、二阶涡动频率近似为1 260 r/min，24 000 r/min；随着安装偏心增大，低频涡动幅值基本呈现先增大后减小的趋势，但一阶涡动幅值随安装偏心增大逐渐减小。

3)涡轮端轴承轴向位置对轴系的失稳转速影响较大；泵端、涡轮端轴承轴向位置变化时失稳转速变化规律相反，泵端轴承远离密封结构时失稳转速减小，而涡轮端轴承远离密封结构时失稳转速增大。

[1]WYSSMANN H,JENNY R,PHAM T.Prediction of stiffness and damping coefficients for centrifugal compressor labyrinth seals[J].ASME Journal of Engineering for Gas Turbines and Power,1984,106(4):920-926.

[2]NOSAKA M.Self-lubricating performance and durability of ball bearings for the LE-7 liquid oxygen rocketturbopump[J].Lubrication Engineering,1993,49(9):677-688.

[3]TIWARI M,GUPTA K,PRAKASH O.Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J].Journal of Sound and Vibration,2000,238:723-756.

[4]CHIRLDS D W.The space shuttle main engine high pressure fuel turbopump rotordynamic instability problem[J].Journal of Eng.Gas Turbines Power,1978,100(1):48-57

[5]ARGHIR M,FRENE J.Rotordynamic coefficients of circumferentially grooved liquid seals using the averaged Navier-Stokes equations[J].ASME Journal of Tribology,1997,119:556-567.

[6]MUSZYNSKA A,BENTLY D E.Frequency-swept rotating input perturbation techniques and identification of the fluid force models in rotor/bearing/seal systems and fluid handling machines[J].Journal of Sound and Vibration,1990,143(1):103-124.

[7]BROMMUNDT E,OSTERMEYER G P.Stability of a rotor partially filled with liquid and attached to an anisotropically mounted shaft[J].Ingenieur-Archiv,1986,56(3):379-388.

[8]HOLM-CHRISTENSEN O,TRAGER K.A note of instability caused by liquid motions[J].Journal of Applied Mech.,1991,58(4):801-811.

[9]ZHANG W.Dynamic stability of a rotor filled or partially filled with liquid[J].Journal of Applied Mech.,1996,64(1):101-105.

[10]沈紫乐,李凌均,雷新望.转子系统中轴承位置对联轴器不对中量影响的研究 [J].矿山机械，2011,39(9):113-116.

[11]牛忠俊,花春.轴系横向振动边界参数的确定及轴承位置优化 [J].2011泰州职业技术学院学报,2011,11(3):110-114.

[12]白长青,许庆余,张小龙.滚动轴承-火箭发动机液氢涡轮泵转子系统的动力特性分析[J].航空学报,2006,27(2):258-261.

[13]应桂炉.氢涡轮泵试验振动分析 [J].导弹与航天运载技术,1995(5):40-46.

[14]祝长生.支承刚度各向异性部分充液转子系统的稳定性[J].航空动力学报,2000,15(4):431-434.

[15]张大义,母国新,洪杰.航空发动机转子支承系统刚度计算中的几个问题[J].战术导弹技术,2005(2):20-23.

[16]窦唯,刘占生.液体火箭发动机涡轮泵转子弯扭耦合振动研究[J].火箭推进,2012,38(4):17-25.

[17]黄智勇,胡钟兵,李惠敏.大功率、高转速、高扬程涡轮泵振动分析与减振研究[J].火箭推进,2005,31(6):1-6.