利用半导体InGaN/GaN量子阱的高效太阳电池

田燕

（宁夏大学 物理电气信息学院，宁夏 银川 750004）

随着第三代太阳电池的发展，对量子结构太阳电池的研究成为提高太阳电池效率的前沿热点问题.特别是近年对量子阱结构的研究，显示了量子阱结构非常适合应用于太阳电池中，它能够提高太阳电池的整体效率[1].

20世纪90年代，Barnham等[2]发展了基于量子阱结构的太阳电池，将量子阱引入Pin型薄膜太阳电池的本征层，使得这种太阳电池的效率提高到14%，而经过研究者大量的数学理论计算和实验研究，目前量子阱太阳电池的实验室效率已超过25%.Bremner等人的研究表明，量子阱太阳电池的理论极限效率可达到63%.

总之，经过对量子阱结构的太阳电池的研究，发现包含了大量而复杂的量子现象，而这些发现对提高太阳电池的效率有极其重要的意义.

1 量子结构太阳电池的结构模型

1.1 InGaN量子阱结构模型

图1 pin结型的能带结构图Fig.1 Band structure of pin junction

图2 InGaN量子阱电池的阱层结构Fig.2 Trap layer structure of InGaN quantum well battery

量子结构的太阳电池，其电池结构通常我们认为是一个p-i-n结[3]，其中本征层（i层）一般嵌入量子阱结构（见图1），量子阱是以生活中的井为示例，即中间的势阱层是以窄带隙的InGaN材料，两边的势垒层是以宽带隙GaN材料，其中带隙的宽度表示阱的深度，即带隙越窄表示阱越深，这样就构成一个量子阱，据此我们可以提出一个如图2所示的InGaN/GaN量子阱结构.而第一性原理和细致平衡理论分析计算其理论极限效率为其实验研究提供理论依据.而对于其量子阱的结构见图2，两边的GaN层即为势垒层，而中间的InGaN即为是阱层.对于一些载流子的吸收，由于低迁移率都可以被包含在细致原理平衡模型中，而细致平衡原理模型一般又与Shockley-Queisser极限相联系，是基于光流量的输入和输出的细致平衡.然而，细致平衡原理是非常广泛的，对细致平衡偏离的不可逆性之随机热力学量度[3]，SQ极限仅仅依靠于单一的细致平衡对.光子流量和发射的光子流量一般是相等的，即为a(E) φbb(E ).由于SQ极限在某种程度上的兼容性，可以将细致平衡原理的这一概念扩展到任何过程中，设计一个有限迁移率的太阳电池模型是可能的，对于高迁移率的载流子其结果一样.对于这一模型光子的循环确保了SQ极限的兼容性.包含光子循环细致平衡模型是由Mattheis J et al[4]确立的.但这只是对严格的p-n结的注入情况.

1.2 InGaN材料特性

InGaN材料是直接带隙材料，具有制作高效率太阳能电池的潜力.InGaN材料太阳能电池带宽范围从0.7eV到3.4eV范围内连续可调，几乎覆盖了整个太阳光波段，另外，抗辐射性能好.因此，In-GaN更具备制作高效率太阳能电池的特性，成为了目前研究的热点.表1是InxGa1-xN材料的相关参数.

表1 InxGa1-xN材料的相关参数Tab.1 Relevant parameter of InxGa1-xN material

2 原理及其理论分析

2.1 相关原理

2.1.1 第一性原理

由于材料的电学性质、光学性质和基本的原子结构一样，是一个从头开始的密度泛函理论框架模型，可以改变包括局域密度近似在内的相关效果[5].在量子阱结构中，其模拟中应用密度泛函原理，所有电子的波函数和电动势的雁电势等都可以描述.当赫尔曼-费恩曼作用力作用后处于平衡状态的原子结构，总能量的极小化可能导致材料的晶格常数发生变化.为了改变电子和量子阱的强度，这里需要探究合适的晶格常数.

在超晶格的量子结构中，Ev（k）和φvk（x）是Kohn-Sham方程的本征值和本征函数，v为价带指标，C为价带，V为导带，波矢k在超晶格结构的布里渊区中是不一样的，这样类电子和类空穴将会消失.这一缺陷对带隙和光跃迁能量具有显著意义[6]，它可以对准粒子理论进行校正.用剪刀操作法解释空态和占有态的带隙和相应的带宽（EC（k）-EV（k）+Δ），值是封闭的.结果，SQ近似原理的结果是介电函数εa（ω）的虚部：

其中ω为角频率，q为元电荷，Ω为电池的体积，a为笛卡尔极化常数，对于单个的准粒子理论的态密度：

在多量子阱结构中硅层的量子局限效应导致电子态的重构.首先产生一个小的直接带隙，但是振子强度发生在E0以下的有限体积内，其迁移能量大约为3.1eV.k波矢的选择定则的对称性对来源于介电常数的吸收系数a（E）有巨大的影响.然而，除了光吸收系数外和电子空穴对的产生之外，太阳电池的效率还有电子和空穴的迁移率来决定.因此，研究的类似于大量的硅的例子的态密度效率为：

其中，k为波尔兹曼常数，T为绝对温度.在室温下非简并态的KT=25mev.对于电子和空穴的NC（NV）由最低导带能量（最高价带能量）和单个的准粒子理论态密度即（2）式来决定其极限.用相应带指数来描述DOS的效率分布，它们相当于所有方向上的平均数量.在大多情况下，各向同性的电子和空穴的有效质量分别为mn和mp用（3）式来表示，则有：

2.1.2 Shockley-Queisser极限

任何光伏吸收材料最基本的要求是能够吸收一定范围内的光子能量，计算半导体吸收的光子能量，需要知道吸收系数和射入的光子的频率.各向同性吸收系数a（E）以单个的数量和带隙Eg为特征的.理想的吸收率是由零以上的带隙和一以下的带隙来定义的.即，在SQ极限下光电流为：

但是，仅仅只有光电流对计算太阳电池的转化效率是不够的，在SQ极限中，还需要太阳电池中只有发射的光子流量决定的复合电流.假定太阳电池交接处有一位V的电压可以发射光子，由下面式子给出[13]：

而一半以上的太阳电池的光谱由黑体辐射所决定，由下式给出[7]：

其中C为光速，公式（7）来自于基尔霍夫定律[8].这说明固有的吸收率和辐射系数都相等.

由太阳电池发射的光子通量φem必须来自于一个重组电流Jrec,SQ=q∫φemdE，如果我们从等式（7）的指数项将前因子分离出来，则饱和电流密度J0,SQ=Jrec,SQ/[e xp(q V)-1] ，即：

则太阳电池的J/V曲线由下式给出：

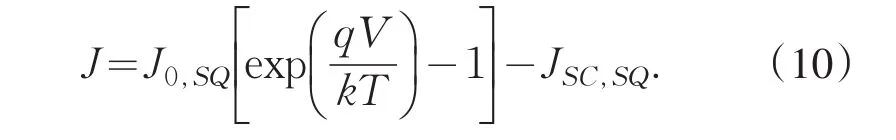
在J/V曲线中，其效率遵循电流功率密度P=JmpVmp，最大功率点（Jmp，Vmp）和射入的最大光功率密度是相对的，利用吸收体的跃迁，公式（6）～（10）可作为带隙函数计算单结或多结太阳电池的效率[9].

为了计算吸收率，我们假定前表面的反射率Rf=0，后边面的反射率Rb=1，从表面到后面的厚度为d，则吸收率由下式决定：

其中tlamb(E)=1/n2,n为折射率，其中：

前面的反射率是从背面到前面的离子输运整合：

2.1.3 Pin结的细致平衡原理

由于量子结构太阳电池的电池结构相当于pi-n结，而i层是量子阱或者量子点结构的嵌入，则细致平衡原理为其实验研究提供了理论依据.为了计算深吸收体单结的载流子浓度，必须明确这里三个不同的等式（电势和空间电荷以及电介质常数之间的关系），描述载流子的产生和重组的连续性方程，下式给出的在单pin结中的电子浓度n和空穴浓度p的漂移扩散方程：

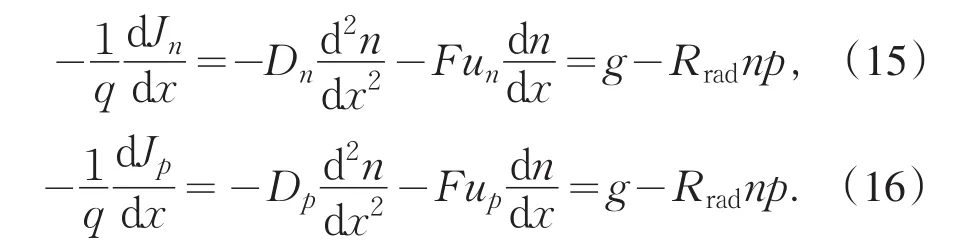
Jn和Jp分别是电子和空穴密度，E是电场强度，g是产生率，Dn,p=un,pkT/q,un和up是电子和空穴的迁移率，kT/q是热电压，辐射复合系数Rrad.由于细致平衡原理和Roosbroeck-Shockley相联系，如下：

其中ni是本征载流子浓度.

本征载流子浓度对器械性能有不同的影响.高本征载流子浓度增加载流子的输运数量.因此，由于载流子的输运不足导致短路电流降低，是有效迁移率朝较小的方向转变.但是，高的本征载流子浓度也可以增加费米能级辐射和非辐射的重组，因为自由载流子的增加可以增加重组.因此，高的本征载流子浓度可以增加开路电压.吸收率和黑体光谱中的n2i有一个固定值，这意味着在较低带隙中这一直观假设导致较低的开路电压.如果所有情况保持一样，通过等式（17）我们可以理解两点：第一，通过增加左边的禁带宽度Eg和ni来增加重组率和减小开路电压；第二，我们可以将φbb转向最大化导致右边的积分增大.当我们从辐射和发射计算迁移率时（等式右边）辐射极限时只有一种可能，当少数载流子的寿命保持不变，高的本征载流子浓度会产生高的重组率，对无辐射重组也是一样的.

2.2 理论分析

2.2.1 光学极限

从第一性原理计算，可以得到效率极限、态密度、各向异性的大量电子的输运方向.第一步，只集中在材料的光学性质上.例如，吸收系数和反射率.在原始的SQ原理中，太阳电池的辐射极限只能从带隙和假想的吸收步骤中计算.但是，在实际的太阳电池中带隙涂层有一个极限厚度和效率.随着振子强度增强，经过讨论只有在无限厚的吸收体中增加吸收系数将会丢失.因此，需要计算有限厚度的辐射极限，这就要求吸收层具有某一确切的厚度，就像典型的薄膜非晶硅计算一样.而我们主要讨论厚度和光电流之间的关系.式（11）是朗伯特算法计算光陷阱的极限吸收率的公式.另外，计算吸收率需要知道吸收体的光的折射系数n.这是因为在介质中光子态密度和n2有关.与在空气和在真空中相比，呈现等向分布的电磁波光子在介质中其浓度会比较高.因此，会产生一个路径长度.对于折射定律以及全反射来说，通过来定义朗伯表面的传输量，即等式（12）中的变量.用折射率nSL表示，从而来计算两种材料组成的新材料的折射率：

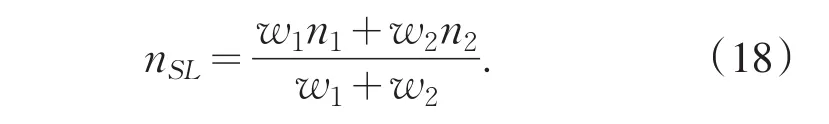
其中n和w分别是两种材料的折射率和超晶格厚度.和超晶格相比，为了避免大的误差，可以根据超晶格的不同厚度来比较合理化的选择折射率，从而根据折射率从第一性原理来计算吸收率，等式（3）和（12）～（15）来计算吸收率，等式（7）～（11）可以计算高辐射迁移率.这意味着对一个很好的结晶硅电池的电池底层是一个两端串联的结构的太阳电池，能够实现较好的带隙和短路电流.

2.2.2 迁移率极限

到目前为止，我们计算SQ极限是源于从第一性原理计算吸收效率计算的.接下来的这种模型描述是用有限迁移率计算辐射极限的，和SQ理论的纯光学计算相比较，细致平衡原理需要额外的参数.例如，迁移率和本征载流子密度等.其中，本征载流子密度是根据有效的态密度和光传导NC和NV以及不同材料的价带和带隙宽度来计算的，计算公式见式（19）：

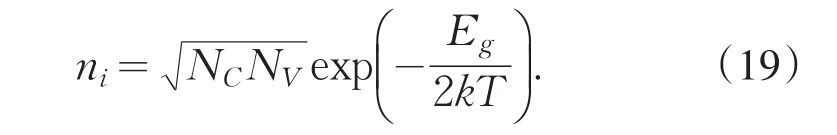
细致平衡原理是是在自由输运的高迁移率的情况下做出来的，其结果和一般的SQ极限是一样的.JSC、VOC和效率是根据等式（7）～（11）的辐射平衡来计算的，其迁移率是一个很好的无限近似.

电子和空穴的态密度和效率不仅和本征载流子的密度相关，而且还可以估计自由电子的迁移率，布洛赫迁移由下式计算：

τsc是扩散时间.为了从有效质量计算计算迁移率，我们还需要估计扩散时间τsc.有科学家研究了使硅量子点嵌入到电介质的问题.因此，我们将其扩散时间命名为相同的值，这样扩散时间和有效质量联系在一起.

在单一的辐射重组极限中的电子和空穴的迁移率的短路电流，这里电子和空穴的迁移率被认为是相等的.下面我们探究的是在无辐射重组需要的迁移率和估计的迁移率对高电流之间的差别.

2.2.3 无辐射重组

最后一步是从理想化期间到实际模型是无辐射重组的引入和窗口层吸收的归结.无辐射重组是一个复合率模型.

根据Shockley-Read-Hall的数据，τn是电子的寿命，τp是空穴的寿命，这两个常数一般是相等的，即τn=τp=τ.

根据相关资料可以得出随着寿命的变长其效率是单调递增的，但是随着寿命的变长其效率的增长速度是不同的.在寿命小于1ns时比寿命较长时增加的快.这可以通过不同的开路电压、填充因数FF、短路电流密度等来解释，当寿命大于1ns时短路电流密度是保持不变的，当寿命变短时短路电流开始急剧下降.相反，随着开路电压的增加其效率的增长率逐渐增加.对于填充因子的影响，唯一不同的是短路电流密度在寿命大于10ns时有粗略的衰减.和短路电流密度相比对其寿命的影响是非常灵敏的，这是由于载流子的收集主要依赖于嵌入的pin结.因为入射场温度高于零度时电压大于节点电压的最大值，短路电流的收集比在给定的迁移率与寿命乘积更加有效.随着迁移率与寿命乘积的值的增加，会收集到更高的电压.

我们感兴趣的是从超晶格结构中估计载流子的寿命，为了从测量的钝化后载流子的寿命估计其表面复合速率，Sproul[10]给出表面复合速率和载流子寿命的关系：

其中ω是整个晶片的厚度，s是两表面之间的表面复合速率，D是载流子扩散常数.如果整个晶片厚度ω减小，则表面扩散系数将会消失.假设ω为由几个硅和二氧化硅量子阱构成的超晶格的厚度，一个量子阱的寿命可以由下式给出粗略的近似，并且，其中NW是对于一个平行的链接几个量子阱的个数.为了估计寿命的数量级，假设一个表面钝化非常好的量子阱以及这样的100个量子阱的常数为ω=2nm和s=10 cm/s，则载流子的寿命τs=100ps，和需要的相差一个或者两个数量级.不管是对太阳电池量子阱兼容超晶格的计算还是对不同厚度极小化的复合速率，这都是很重要的问题.

3 结论

根据以上相关理论并且利用TiberCAD软件对图2所示的InGaN/GaN量子阱结构进行了模拟计算，得出了相应理论数据，表2、表3、表4分别计算了Eg1，即InxGa1-xN中铟组分的含量即x的取值不同时，根据表1分别得到了带隙为1.39 eV、1.73 eV和1.89 eV时的太阳电池结构，并对其进行了相应的模拟计算得到太阳能电池的光电转换效率.作为对照，每个表的最后一行势垒和势阱相等，此时量子阱的作用消失，计算得到的转换效率与理想单结太阳能电池效率一致，检验了量子阱结构细致平衡模型和计算方法的可靠性.

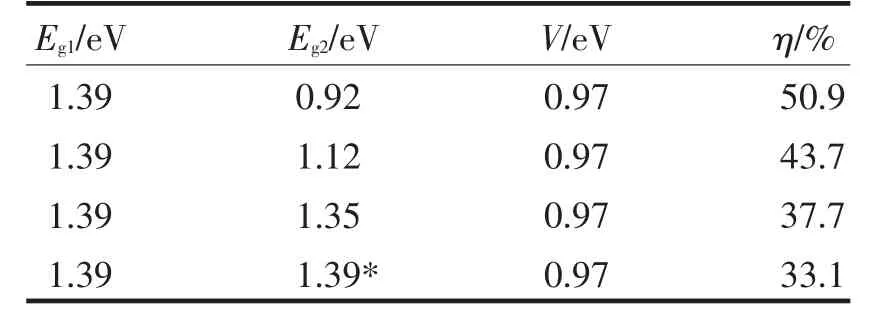
表2 InGaN量子阱太阳能电池参数与转换效率(A)Tab.2 InGaN quantum well solar cell parameters and the conversion efficiency(A)

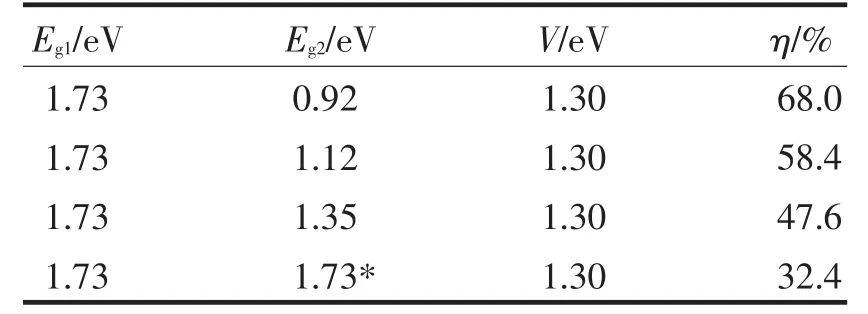
表3 InGaN量子阱太阳能电池参数与转换效率(B)Tab.3 InGaN quantum well solar cell parameters and the conversion efficiency(B)

从计算结果可以看出，势垒禁带宽度不变，随着势阱禁带宽度的减小，太阳能电池的转换效率逐渐增大，如果势阱禁带宽度不变，太阳能电池转换效率随着势垒的增加而增加.文博[11]等人使用太阳能电池的电流电压方程方法，计算了没有引入量子阱结构的InGaN材料叠层太阳能电池的效率.Eg1为1.73 eV，Eg2为1.12 eV的双结太阳能电池的效率为36.6%，Eg1为1.89 eV，Eg2为1.35 eV，Eg3为0.92 eV的三结太阳能电池的效率为41.3%.通过引入量子阱结构，InGaN材料太阳能电池转换效率得到大幅提高.通过细致平衡模型计算，当势垒为1.73 eV，势阱为1.12 eV时，电池转换效率为58.4%；势垒为1.89 eV，势阱为1.35 eV时，电池转换效率为55.3%.可见，InGaN材料量子阱模型的光电转换效率，比未引入量子阱结构的叠层太阳能电池的光电转换效率有很大提高.即通过在电池中引入量子阱结构，可以获得更高的光电转换效率，量子阱结构对提高电池效率有明显优势.

表4 InGaN量子阱太阳能电池参数与转换效率(C)Tab.4 InGaN quantum well solar cell parameters and the conversion efficiency(C)

[1]张小宾.InGaN太阳能电池理论模拟及制备研究[D].北京：中国科学院半导体研究所,2010.

[2]Kerr M J,Campbetl P,Cuevas A.Lifetime and efficiencylimits of crystalline silicon solar cells[C].Photovoltaic specialists conference,conference Record of the Twenty-Ninth IEEE,2002：438-441.

[3]包科达,刘秀华.试论热学课程中的平衡态概念及其与细致平衡原理的关系[J].大学物理,1997,16(7)：35-39.

[4]Mattheis J,Werner J H,Rau U.Finite mobility effects on the radiative efficiency limit of pn-junction solar cells[J].Phys Rev B,2008,77：8.

[5]李震宇,贺伟,杨金龙.密度泛函理论及其数值方法新进展[J].化学进展,2005,17(2)：192-202.

[6]Aulbur W G,Jönsson L,Wilkins J W.Solid State Phys：Advances in Research and Applications[J].Aca-demic,San Diego,2000,54：1-281.

[7]Adolph B,Gavrilenko V I,Tenelsen K,et al.Nonlocality and many-body effects in the optical properties of semiconductors[J].Phys Rev B,1996,53：9797-9808.

[8]Würfel P.The chemical potential of radiation[J].Phys C,1982,15：3967.

[9]林硕,沈晓明,张保平.InGaN单结太阳电池中的浅能级杂质的理论计算和模拟[J].科学通报,2010,26(15)：1446-1452.

[10]Martí A,Araújo G L.Limiting efficiencies for photovoltaic energy conversion in multigap systems[J].Sol Energy Mater Sol Cells,1996,43：203-222.

[11]文博,周建军,江若琏.InGaN太阳能电池转换效率的理论计算[J].半导体学报,2007,28（9）：1392-1395.