和星型图相关图的巧妙性
2013-10-12杨伟芳李大超
杨伟芳,李大超
(海南师范大学 数学与统计学院,海南 海口 571158)
图论起源于著名的柯尼斯堡七桥问题.在18世纪30年代,一个非常有趣的问题引起了欧洲数学家的浓厚兴趣,这个问题要求遍历普鲁士的哥尼斯堡七桥中的每一座桥恰好一次后回到出发点,欧拉证明了这是不可能完成的.此后,欧拉发表了著名的论文《依据几何位置的解题方法》,这是图论领域的第一篇论文,标志着图论的诞生.而标号图是图论的研究课题之一,标号图实质是根据一定的映射规则,给图的顶点或边赋值,在根据条件得到所需要的结论,所以标号图就是一种方法,它是解决实际问题的一种技巧,即人们把实际问题通过图的设计,建立起图,用顶点和边表示实际问题中的量与量之间的关系,然后根据实际要求,通过一定的规则,给图的顶点或者边,或者顶点和边赋值,从而反映出实际问题的需求.
标号图中有一类极有趣的研究课题就是巧妙图,由于它的趣味性和应用性,很快得到了人们的重视.
1 基本概念
定义1[1]一个简单图G=(V,E)被称为巧妙的,若存在单射 f∶V→{0 ,1,2,…,|E |},使得导出映射f+(e)=f(x)+f(y)(m od|E |)就是E到{0,1,2,…,|E|-1}的双射,这里,e=(x ,y)∈E.
定义2[2]如果删去树T的所有悬挂点及与其相关联的边后所得的图是一条通路或一个孤立点,则称T是一个毛毛虫.这条通路或这个孤立点被称为T的路.
定义3[2]路是孤立点的毛毛虫就是星.含有n个悬挂点的星记作Sn(见图1).

图1 Sn图Fig.1 Sn
定义4[3]设Sm是具有m条边的星型图,将Sm的中心点与Cn的任意点粘合所得到的图记为Cn⊗Sm.
定义5[4]设Sm是具有m条边的星型图,将Sm的任一个非中心点与Cn的任意点粘合所得到的图记为Cn⊗Sm.
定义6[5]是n条边的星型图的的细分图(见图2).

图2 图Fig.2
2 定理证明
文[1]证明了C2k+1⊙Sm是巧妙图,我们有
定理1 对任意的正整数n(n≥3)和m,Cn⊗Sm是巧妙图.
证明 设Cn上的点按邻接关系依次为x1,x2,…,xn,Sm的悬挂点为y1,y2,…,ym,又设xn与Sm的中心点粘合(见图3).
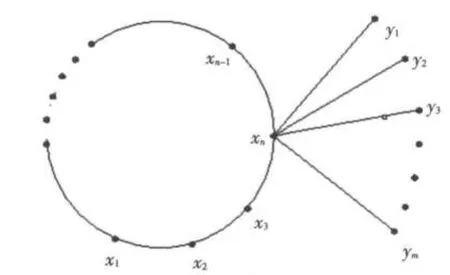
图3 Cn⊙Sm 图Fig.3 Cn⊙Sm
情形1 当n≡1(mod2)时,由文献[1]知是巧妙图.
情形2 当n≡0(mod4)时,定义 Cn⊙Sm的顶点标号f如下:

可以验证,以上标号f是Cn⊙Sm的巧妙标号.
情形3 当n≡2(mod4)时,定义 Cn⊙Sm的顶点标号f如下:

可以验证,以上标号f是Cn⊗Sm的巧妙标号.
综合情形1-情形3知:对任意的正整数n(n≥3)和m,Cn⊗Sm是巧妙图.
定理2 对任意的k和m,C4k⊗Sm和C8k+6⊗Sm是巧妙图.
证明 (1)对于C4k⊗Sm,设C4k的顶点按邻接关系依次为 x1,x2,…,x4k,Sm的非中心点为 y1,y2,…,ym,中心点为y0,x4k与y1粘合(见图4),定义其顶点标号f1如下:
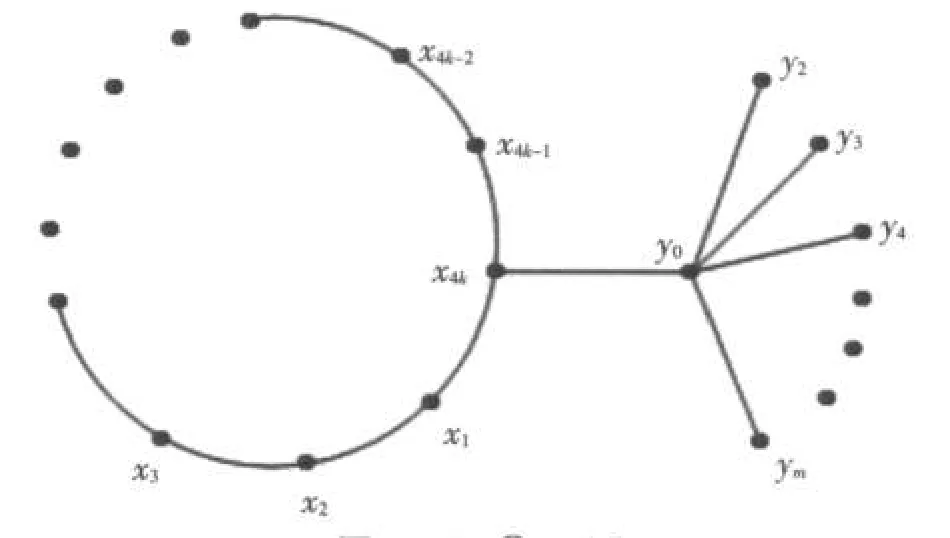
图4 C4k⊗Sm图Fig.4 C4k⊗Sm

可以验证,以上标号f1是C4k⊗Sm的巧妙标号.
(2)对于C8k+6⊗Sm,设C8k+6的顶点按邻接关系依次为 x1,x2,…,x8k+6,Sm的非中心点为 y1,y2,…,ym,中心点为y0,x1与 ym-1粘合(见图5).定义其顶点标号f2如下:


图5 C8k+6⊗Sm图Fig.5 C8k+6⊗Sm

可以验证,以上标号f2是C8k+6⊗Sm巧妙标号.
此外,本文还证明了:
定理3 图G4⊗-S3是巧妙图.
证明 设C4上的点按邻接关系依次为x1,x2,x3,x4,S3的悬挂点为 y1,y2,y3,y4,y5,y6,y7,又设 x4与的中心点y1粘合,则图G4⊗-S3有10个顶点,10条边(见图6).定义图的顶点标号f如下:(fx1)=2,(fx2)=0(fx3)=4,(fx4)=1(fy1)=5,(fy2)=6(fy3)=8,(fy4)=9(fy5)=7,(fy6)=3
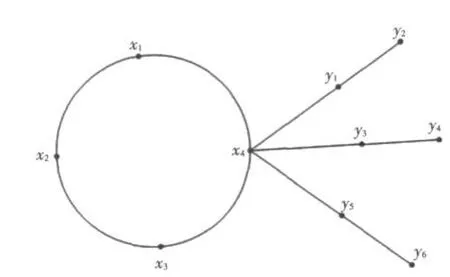
图6 图Fig.6
g(x1,x2)=2,g(x2,x3)=4,g(x3,x4)=5,g(x1,x4)=3
g(x4,y1)=6,g(y1,y2)=1,g(x4,y3)=9
g(y3,y4)=7,g(x4,y5)=8,g(y5,y6)=0
[1]Lee S M,Schmeichel E,Shee S C.On felicitious graphs[J].Discrete Math,1991(93):201-209.
[2]李大超.一类巧妙图的充要条件[J].海南大学学报:自然科学版,1996,14(4):281-285.
[3]冯成进.一类优美图的充要条件[J].曲阜师范学院学报:自然科学版,1983(1):23-29.
[4]孙宗剑,罗簿鹏.塔图的强协调性[J].桂林工学院学报,2006,26(4):589-590.
[5]粱志和.关于图标号问题[J].河北师范大学学报:自然科学版,2000,24(3):300-303.
